Accès Rapide
Introduction
Problème
Depuis une séquence triée, trouver la position exacte d'un élément s'il existe.
Une approche simple consiste à effectuer une recherche linéaire (vérifier chaque élément un par un). La complexité temporelle d'une telle recherche est linéaire : O(n). Une autre approche consiste à utiliser la recherche binaire (dichotomique). Celle-ci offre le même résultat tout en réduisant la complexité temporelle à une croissance logarithmique : O(log n).
Considérons par exemple une liste contenant 1 million d'éléments : - Si nous effectuons une recherche linéaire, nous pourrions avoir à effectuer 1 million d'itérations et 1 million de comparaisons. - Avec une recherche dichotomique nous le trouverons à coup sûr avec pas plus de 20 itérations et 20 comparaisons (5000 fois plus vite asymptotiquement !).
Applications
- Recherche d'un index au sein de séquences énormes (base de données).
- Idée clé dans les arbres binaires, une structure de données très importante et utilisée.
- Définir les racines carrées de nombres (e.g. méthode de Newton).
Homonymes
- Recherche à mi-intervalle (Half-interval search)
- Recherche Logarithmique (Logarithmic search)
- Recherche Binaire (Binary search)
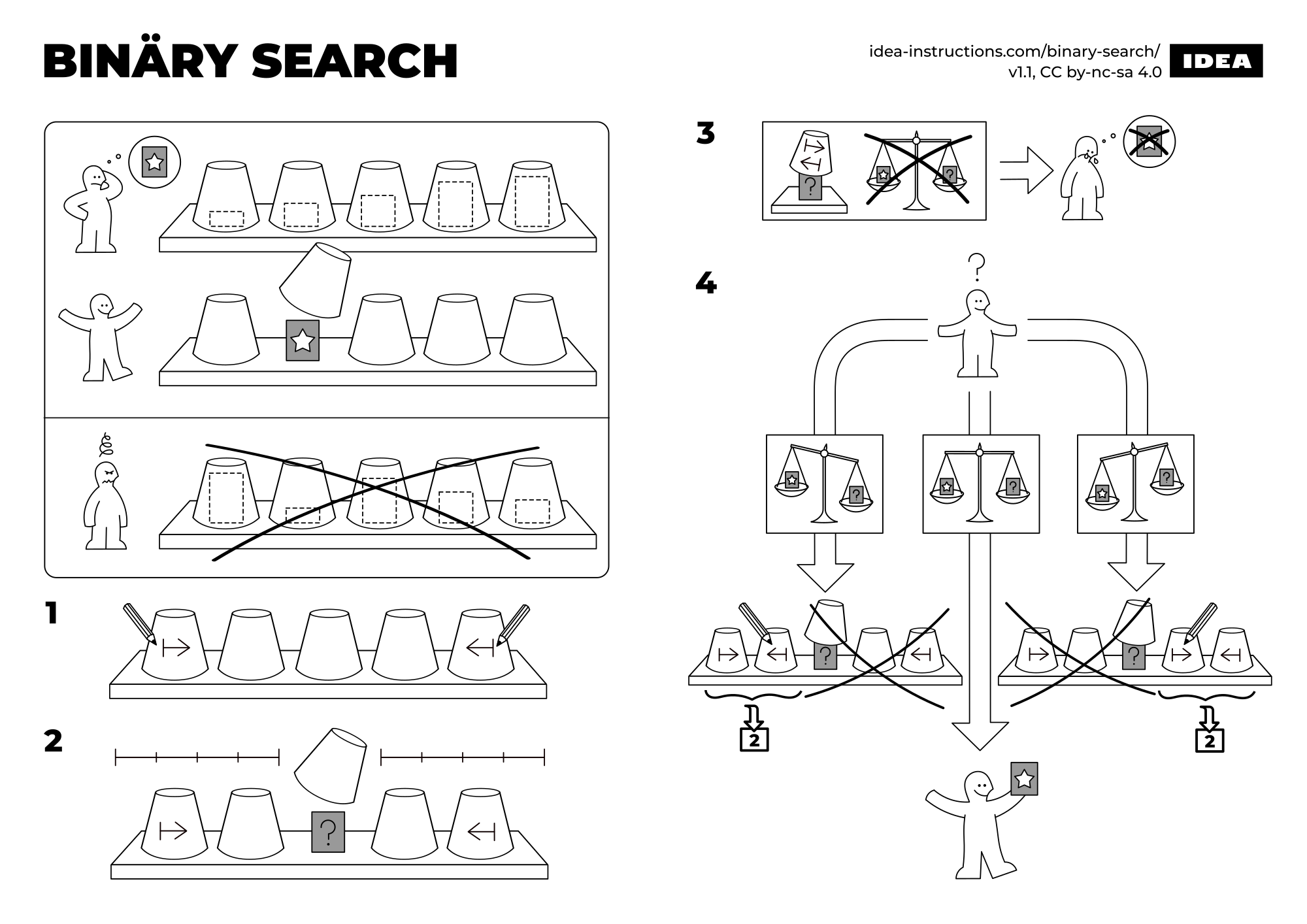
Construction
La recherche binaire est un algorithme régis par le paradigme diviser pour mieux régner (découpe un problème en sous-problème plus simple à résoudre). Il fonctionne en déterminant si la valeur de recherche est inférieure ou supérieure à la valeur se trouvant au milieu de la séquence. Il itère ensuite uniquement sur la moitié inférieure ou supérieure jusqu'à ce que la valeur soit trouvée ou non (la sous-séquence est vide).
Etapes
- 1. Comparer la valeur de recherche avec l'élément au centre.
- 2. Si c'est elle nous avons terminé : renvoyer l'index du milieu..
- 3. Si la valeur est plus grande que la valeur recherchée : refaire la recherche dans la sous-séquence inférieure.
- 4. Si la valeur est plus petite que la valeur recherchée : refaire la recherche dans la sous-séquence supérieure.
Code
Index BinarySearch(Iterator begin, Iterator end, const T key)
{
auto index = -1;
auto middle = begin + distance(begin, end) / 2;
// While there is still objects between the two iterators and no object has been foud yet
while(begin < end && index < 0)
{
if (IsEqual(key, middle)) // Object Found: Retrieve index
index = position(middle);
else if (key > middle) // Search key within upper sequence
begin = middle + 1;
else // Search key within lower sequence
end = middle;
middle = begin + distance(begin, end) / 2;
}
return index;
}
Visualisation
L’analyse étant assez triviale, elle est incluse dans le diapo d'images en en-tête de cet article.
Complexité
Temps
Meilleur
La meilleure configuration se produit lorsque l'élément recherché se trouve au centre de la séquence, conduisant ainsi à une complexité de O(1).
Moyen / Asymptotique
Le pire scénario se produit lorsque l'élément recherché ne se trouve pas dans la séquence. Après la première recherche nous itérons sur la moitié inférieure / supérieure jusqu'à avoir une séquence vide. Mettons cela dans une relation de récurrence: $$T(n) = O(1) + T(\frac{n}{2})$$ Le master theorem ou théorème sur les récurrences de partition nous donne : T(n) = O(log n).
Espace Mémoire
La recherche binaire n'utilise aucune mémoire supplémentaire ni ne fait de récursivité. Ainsi, elle a une complexité de O(1) dans tous les cas.





 Jouer en ligne
Jouer en ligne
 Code Source C++
Code Source C++