Communément écrits f ^-1 (x) , elles sont extrêmement utiles pour résoudre tout types d'équations et sont donc un outil très intéressant pour exprimer plusieurs concepts. Ces functions permettent d'inverser les opérations mathématiques (par exemple : somme et soustraction s'inversent, la multiplication inverse la division, les logarithmes inverses exponentiels, etc. ). Chaque fois qu'une nouvelle procédure mathématique est introduite, l’une des questions les plus importantes est de savoir comment l’inverser.

Deux fonctions sont inverses l'une de l'autre si elles se "défont l'une l'autre" dans le sens suivant : si la sortie de l'un est utilisée comme entrée de l'autre, il en résulte l'entrée d'origine.

Nous connaissons tous naturellement une multitude de fonctions de base et leur inverse, En voici quelques-unes:

$$f(x) = 2 * x$$ $$f^{-1} (x) = \frac{x}{2}$$

$$f(x) = x^2$$ $$f^{-1} (x) = \sqrt{x}$$

$$f(x) = cos(x)$$ $$f^{-1} (x) = arccos(x)$$

$$f(x) = ln(x)$$ $$f^{-1} (x) = e^x$$

Une création montrant la symétrie impliquée.

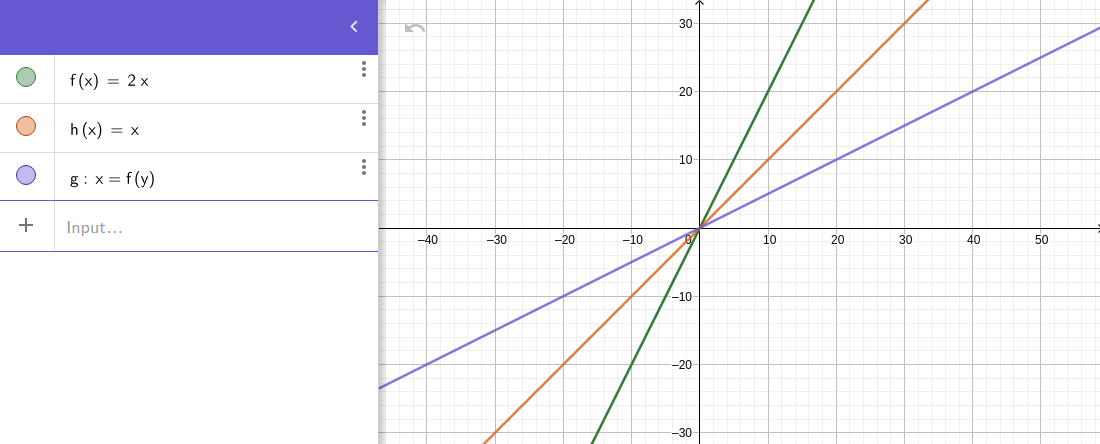
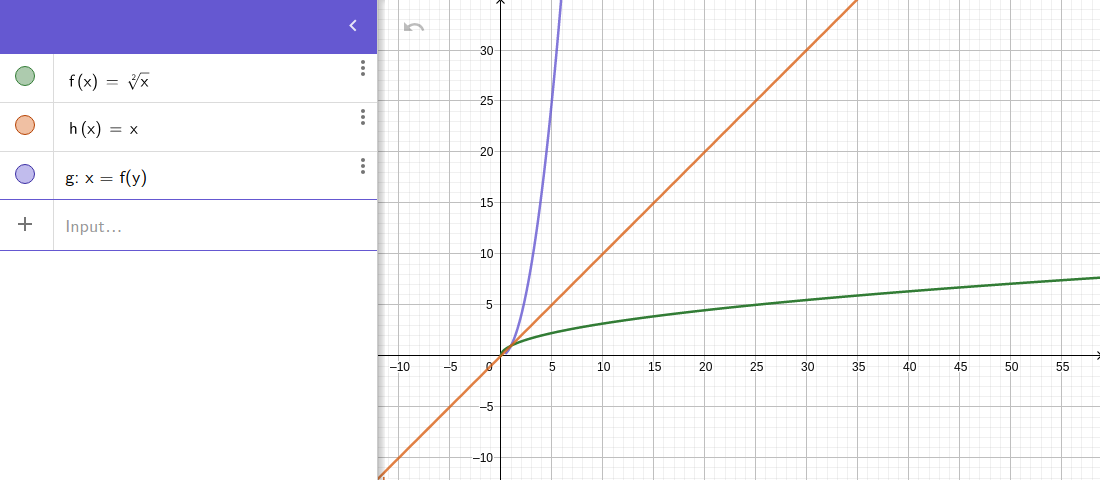
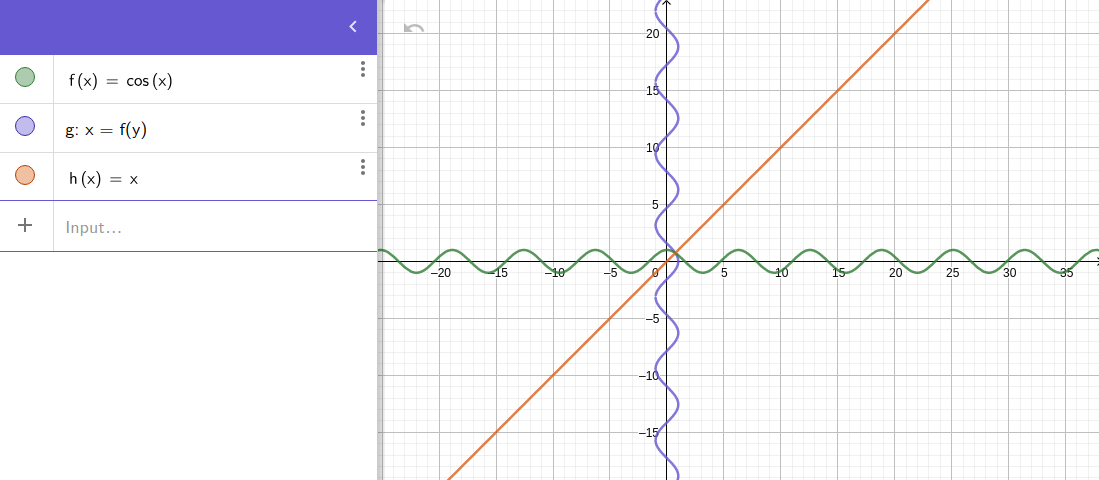
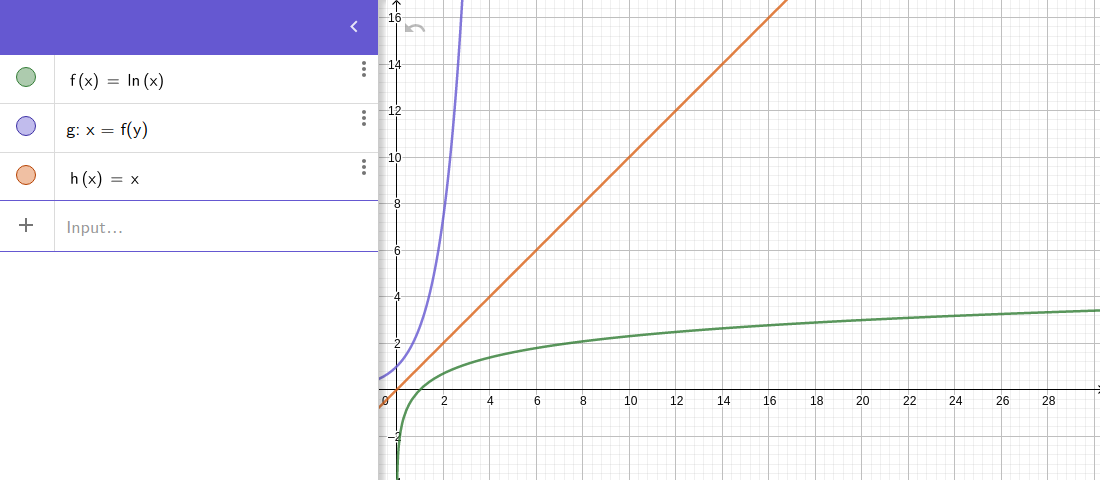
Le graphique de f^-1(x) peut être obtenu à partir du graphique de f en échangeant les positions des axes x et y : cela équivaut à refléter le graphique f par rapport à la ligne y = x.

Le truc cool avec l'inverse d'une fonction, c'est que nous pouvons facilement revenir à la valeur d'origine avec seulement avec le résultat. Lorsque la fonction f(porte) transforme par exemple une porte ouverte en une porte fermée, alors la fonction inverse f^-1(porte) peut l'ouvrir. Ces égalités expriment chacune cette même idée :

$$f(x) = y \iff f^{-1}(y) = x$$ $$f^{-1}( f(x) ) = x \quad et \quad f( f^{-1}(x) ) = x$$