Glossaire
Dimension
Fondamentalement le nombre de dimensions dans l'espace. Les types sont: 2D : la plupart des labyrinthes sont de cette dimension, il est toujours possible de les représenter sur une feuille de papier et de naviguer sans chevaucher aucun passage. 3D : labyrinthe à plusieurs niveaux, où les passages peuvent monter et descendre en plus des directions 2D. Un labyrinthe 3D peut être vu comme plusieurs labyrinthes 2D empilés les uns sur les autres. Dimension supérieure : Il est possible d’avoir des labyrinthes 4D et de dimensions supérieures. Ceux là sont parfois sous forme de labyrinthes 3D, avec des "portails" spéciaux pour parcourir la 4ème dimension (par exemple, les portails d'un temps "passé" ou "futur"). Tissage / Weave (2.5D) : un labyrinthe de tissage est fondamentalement un labyrinthe 2D (ou plus précisément un labyrinthe 2.5D), mais où les passages peuvent se chevaucher les uns les autres. Par exemple, dans des labyrinthes de taille réelle dont des ponts passent au-dessus de chemins.
2D : H.urna Blocks - Globo dans les labyrinthes (Niveau 10)
3D : Labyrinthe 3D trouvable en magasin de jouet
Dimension supérieure : Voici un jeu de labyrinthe 4D, il suffit d'y penser comme un labyrinthe 3D qui peut être modifié au cours du temps (par exemple, nous aurons un contrôleur de temps en plus des déplacements 3D).
Tissage / Weave : un labyrinthe grandeur nature avec des ponts. C'est le labyrinthe de Longleat Hedge construit en 1975 en Angleterre.
Direction
S'il y a une direction, cela signifie que certains passages ne peuvent être parcourus que dans un seul sens. En termes informatiques, de tels labyrinthes seraient décrits par un graphe orienté, par opposition à un graphe non orienté.
Stratégie
Ceci est juste une propriété algorithmique lors de la génération (aucune différence visuelle à la fin). La stratégie peut être divisée en deux types généraux : les constructeurs de murs et les sculpteurs de passages. Le premier commence avec un espace vide où nous ajoutons des murs tandis que le second commence avec un bloc complet dans lequel on sculpte des passages.
Hyperdimension - Hypermaze
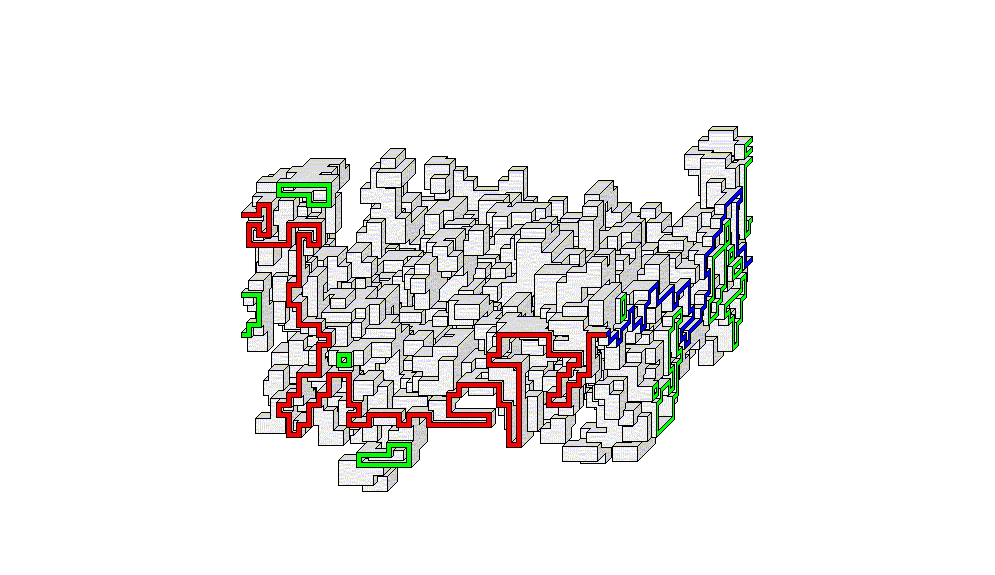
La classe hyperdimension fait référence à la dimension de l’objet que nous déplaçons dans le labyrinthe. Cela est différent de la dimension de l'environnement du labyrinthe lui-même (un hypermaze ne peut exister que dans un labyrinthe 3D ou de dimension supérieure). Un hypermaze augmente la dimension de la résolution et des passages eux-mêmes. Dans un labyrinthe normal, nous déplaçons un point et le chemin derrière nous forme une ligne. Dans un hypermaze, nous déplaçons par exemple une ligne et notre chemin forme une surface !
Hypermaze : Rendu orthographique d'un hypermaze parfait et très complexe (73x73x73 cubes). Notons qu'il y a littéralement des milliards de façons d'organiser la chaîne et de la déplacer dans l'hypermaze. Et parce que c'est un hypermaze "parfait", une seule solution avec une seule configuration initiale fonctionne réellement! Source: Walter D. Pullen using Daedalus Software
Hypermaze - Moitié de solution : Ici, la moitié inférieure du même hypermaze 73x73x73. Source: Walter D. Pullen using Daedalus Software
Hypermaze - Solution unique (surface) : La solution montrant la surface de la solution, celle du chemin emprunté par la chaîne. Le bord coloré en rouge est le bord de la surface : la ligne d'entrée (ou de sortie) dans laquelle la chaîne doit entrer (ou sortir). Le bord coloré en bleu est la même ligne d'entrée / de sortie le long de la face adjacente. Les bords colorés en vert sont des endroits où la surface de la solution remonte et touche brièvement une face frontière. Ceci est juste un effet de rendu pour montrer la surface de la solution coupée à la limite de l'hypermaze lui-même; la surface de la solution réelle n'a bien sûr pas de trous. Source: Walter D. Pullen using Daedalus Software
Routage
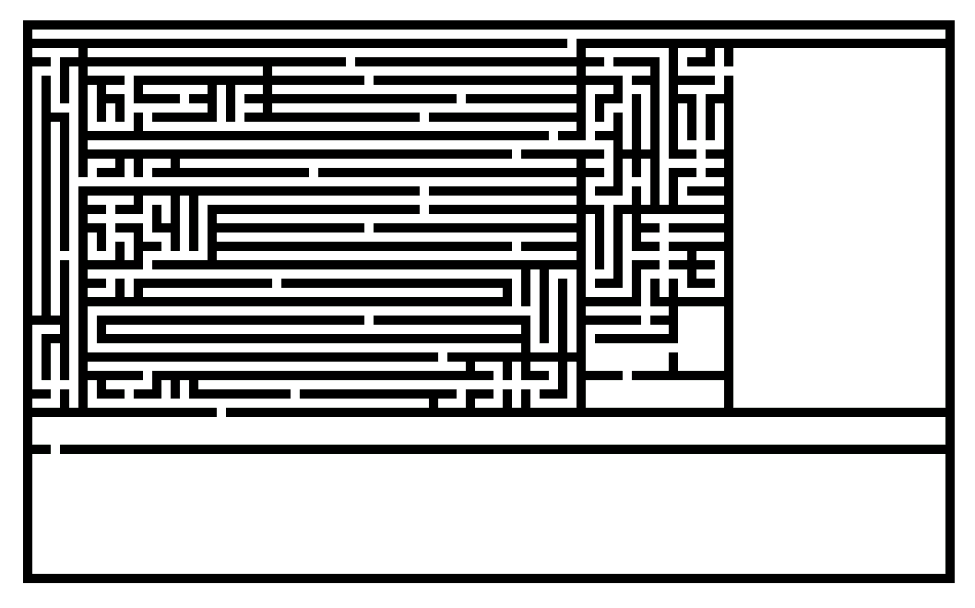
Le routage fait référence aux types de géométrie de passages résultant de la stratégie de génération de labyrinthe. Tresse - Tresse partielle : Un labyrinthe en Tresse, ou "Braid", signifie un labyrinthe sans aucune impasse. Un tel labyrinthe utilise des passages qui s’enroulent (d’où le terme "tresse"). Il nous fait tourner en rond au lieu de se faire bloquer dans des impasses. Un tel labyrinthe peut être beaucoup plus difficile à résoudre qu'un labyrinthe parfait de la même taille. Notons que le terme Tressé peut être utilisé quantitativement. Un «labyrinthe fortement tressé» comprendra de nombreuses boucles. Parfait - Simplement connecté : Toutes les générations de labyrinthe proposées actuellement sur H.urna ont un acheminement parfait. Un labyrinthe "parfait" signifie être sans boucles, sans circuits fermés et sans zones inaccessibles. De chaque point, il y a exactement un chemin vers un autre point : le labyrinthe a exactement une solution. En termes informatique, un tel labyrinthe peut être décrit par un arbre de couverture (spanning tree) . Éparse : Un labyrinthe éparse pour les algorithmes d'ouverture de passages est un labyrinthe qui ne possède pas forcément de passage pour toutes les cellules. Cela revient à avoir des endroits inaccessibles, ce qui est à l’inverse d’un labyrinthe tressé. Un concept similaire peut être appliqué aux algorithmes constructeurs de murs (par exemple, la division récursive), résultant en un labyrinthe irrégulier avec de larges passages et de grandes salles. Unicursal : Un labyrinthe unicursal signifie un labyrinthe sans jonction. Dans de tels labyrinthes il n’ya ni astuces ni impasses : ils ont un seul chemin et sont le plus souvent utilisés pour la relaxation, la méditation ou la spiritualité.
Tressé : Nous ne pouvons pas être coincé dans un cul-de-sac. Source : Wikipedia
Parfait - Simplement connecté : Génération de labyrinthe et inondation montrant la structure ainsi que dualité entre le labyrinthe et sa représentation en arbre couvrant (Spanning Tree). Source : Michaël Jeulin-L avec H.urna Explorer
Éparse : Labyrinthe clairsemé avec de grandes salles produit avec un algorithme de division récursive. Source : Michaël Jeulin-L avec H.urna Explorer
Unicursal : Le mystérieux "Christ dans le labyrinthe" d'Alatri montrant un motif unicursal.
Tesselation
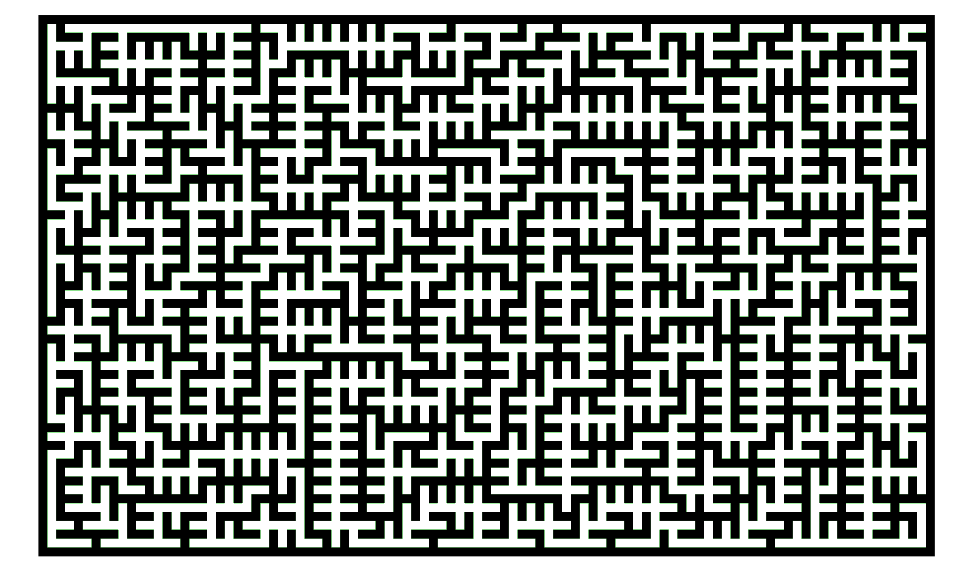
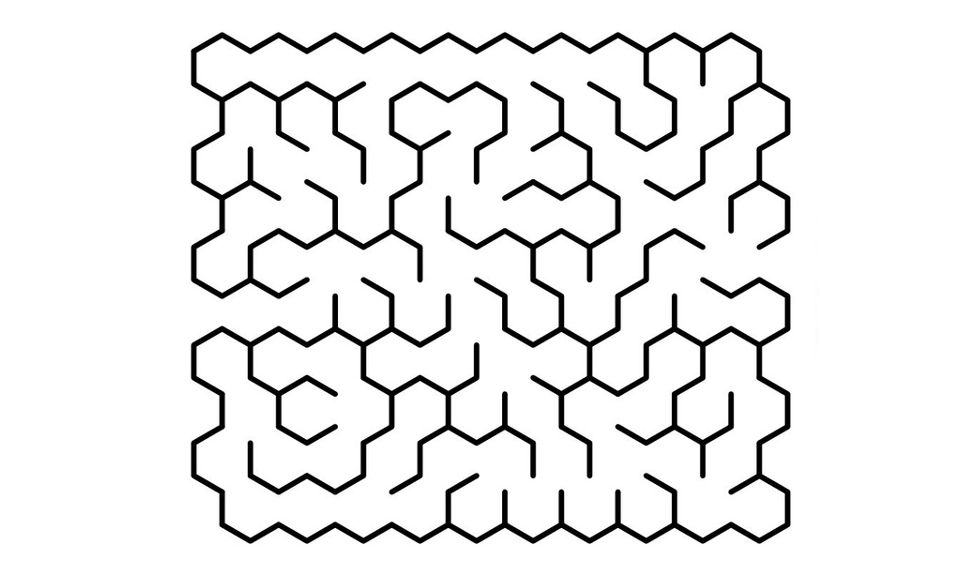
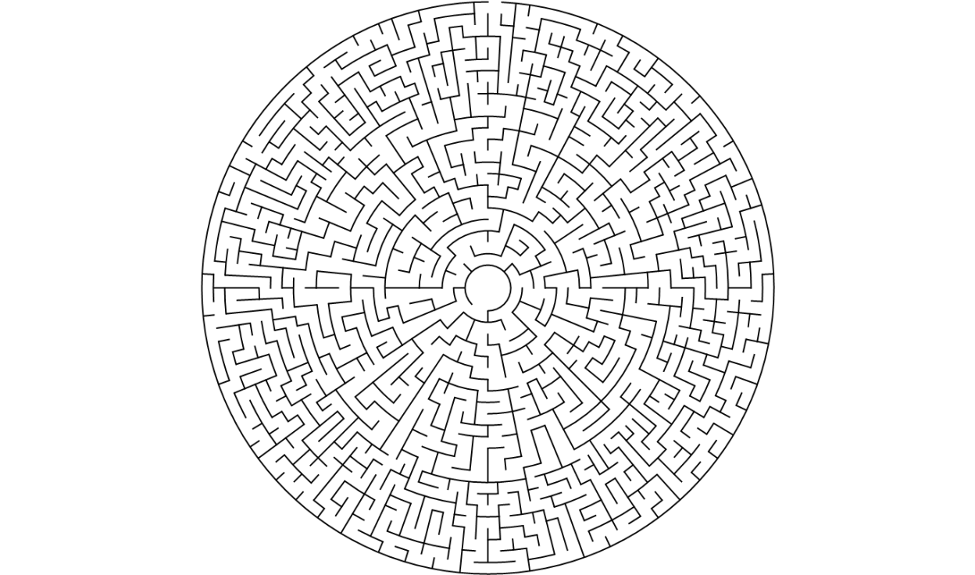
La classe de tessellation est la géométrie des cellules individuelles qui composent le labyrinthe. Nous pouvons imaginer la géométrie que nous voulons. Voici une petite liste des plus communes : Orthogonale (cellules rectangulaires), Fissure (amorphe), Delta (cellules triangulaires), Fractal (récursif), Omega (non orthogonal), Sigma (cellules hexagonales), Thêta (cercles concentriques), Upsilon (cellules octogonales et carrées), Zeta (orthogonal avec les passages en diagonale autorisés) ... Les images parlant plus que les mots, voici quelques-unes de ces tesselations :
Orthogonale : Aussi appelé Gamma, c’est une grille rectangulaire standard où les cellules ont des passages se croisant à angle droit. Source : Michael Jeulin-L avec H.urna Explorer
Delta : un labyrinthe Delta est composé de triangles juxtaposés.
Sigma : un labyrinthe Sigma est composé d'octogones juxtaposés. Source : Dr. Mc Children's Book
Theta : un labyrinthe Theta est composé de cercles concentriques.
Fractal : un labyrinthe fractal est composé de labyrinthes plus petits. Un labyrinthe fractal récursif infini est une vraie fractale et est en effet un labyrinthe infiniment grand. Source : CurvatureOfTheMind
Texture
La classe de texture est subtile et décrit le style des passages quel que soit le routage, quelle que soit la géométrie. Cette propriété est plus qualitative que quantitative. Ci-dessous deux des textures souvent rencontrés avec les générateurs de labyrinthes H.urna :
Bias : Le générateur d'arbre binaire a des passages qui ont tendance à aller dans une direction plus que les autres (sud-est ici). Source : Michael Jeulin-L avec H.urna Explorer
Rivière : texture coulant comme des rivières. Voici un labyrinthe de rivière issu de notre générateur utilisant la recherche en profondeur (DFS). Source : Michael Jeulin-L avec H.urna Explorer
Topolgie
La classe de topologie décrit la géométrie de l'espace dans lequel le labyrinthe existe : Normale : labyrinthe standard dans l'espace euclidien. Planaire : n'importe quel labyrinthe avec une topologie anormale. Des exemples sont des labyrinthes à la surface d'un cube, d'un tore, d'une sphère, etc.