Notre plateau: un labyrinthe aléatoire de 30 x 20 généré à l'aide d'un algorithme de Prim.
Globo (notre mascotte verte au milieu) est le joueur et la capsule bleue est la sortie.

Trace laissée par le joueur utilisant l'algorithme de A* (A-Star) pour atteindre la sortie.

En comparaison, voici la trace laissée par une recherche avec Dijkstra.

Enfin, celle laissée par une recherche en profondeur.

L'algorithme A * (A-Star) optimise celui de Dijkstra en trouvant plus rapidement le chemin le plus court. Il a été inventé par Peter Hart, Nils Nilsson et Bertram Raphael (trois informaticiens américains) et décrits en 1968 dans leur article «Une base formelle pour la détermination heuristique des chemins de coût minimum».

A* est sans doute le meilleur algorithme de recherche de chemin lorsque nous devons trouver le chemin le plus court entre deux nœuds. A* est le standard que tout le monde devrait connaitre.

L'algorithme de Dijkstra fonctionne bien pour trouver le chemin le plus court, il perd cependant du temps à explorer des directions qui ne sont pas prometteuses. A* améliore cela en permettant l'inclusion d'informations supplémentaires dans la fonction heuristique:
 - L'algorithme de Dijkstra utilise la distance du nœud racine.
 - L'algorithme A* utilise à la fois la distance du nœud racine et la distance estimée jusqu'au but.

C'est tout !
En fait, l'algorithme A* n'est qu'une variante de l'algorithme de Dijkstra.

Applications

Comme l'algorithme de Dijkstra, A* est utilisé partout: il est largement utilisé dans les jeux vidéo, dans l'apprentissage automatique, les systèmes de navigation, les véhicules autonomes, le traitement du langage naturel (PNL), etc.

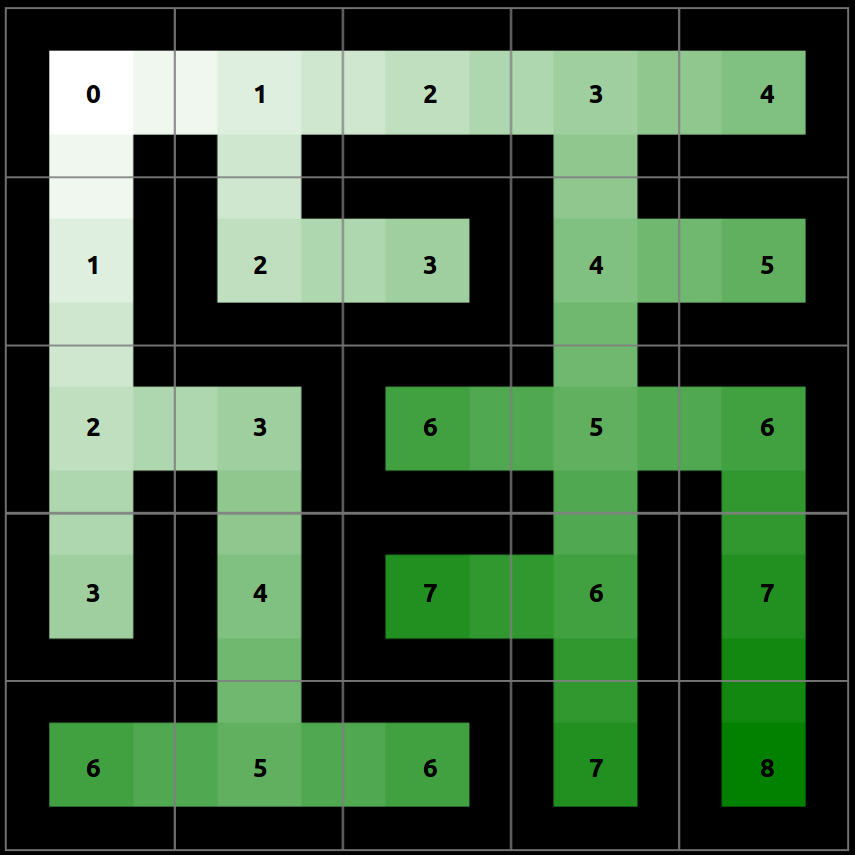
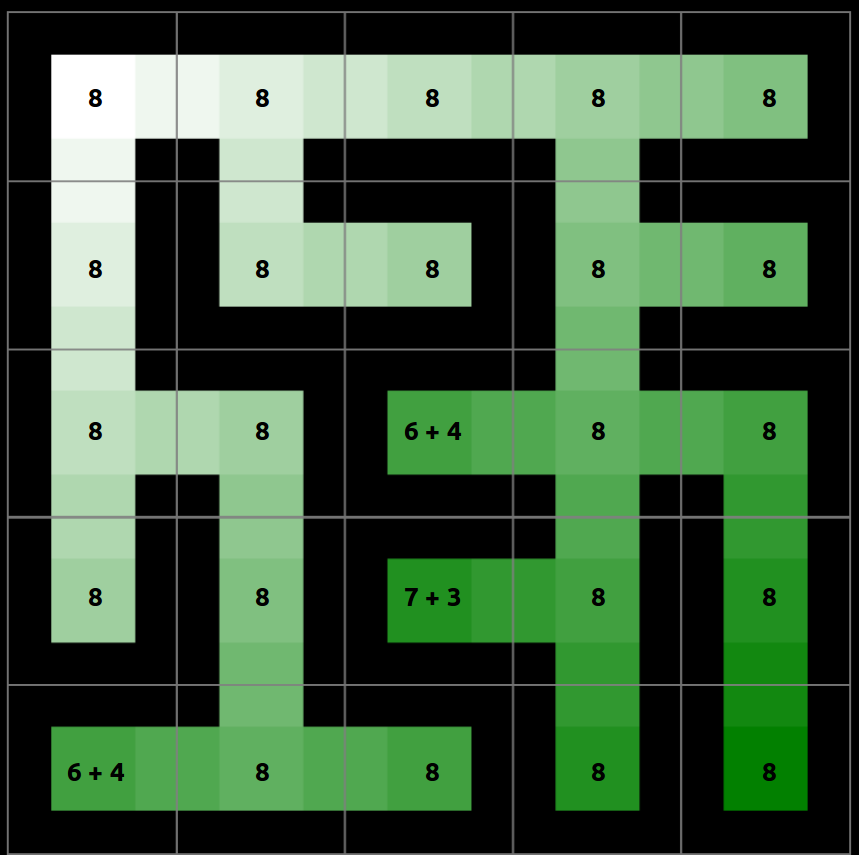
A * sélectionne le chemin qui minimise la fonction suivante: $$f(n) = g(n) + h(n)$$ où:
 - g(n) est le coût du chemin du point de départ au noeud n (distance de Dijkstra).
 - h(n) est le coût estimé du chemin du nœud n au nœud de destination calculé par la distance de Manhattan dans notre cas.

Ok ... mais quelle est cette distance de Manhattan?

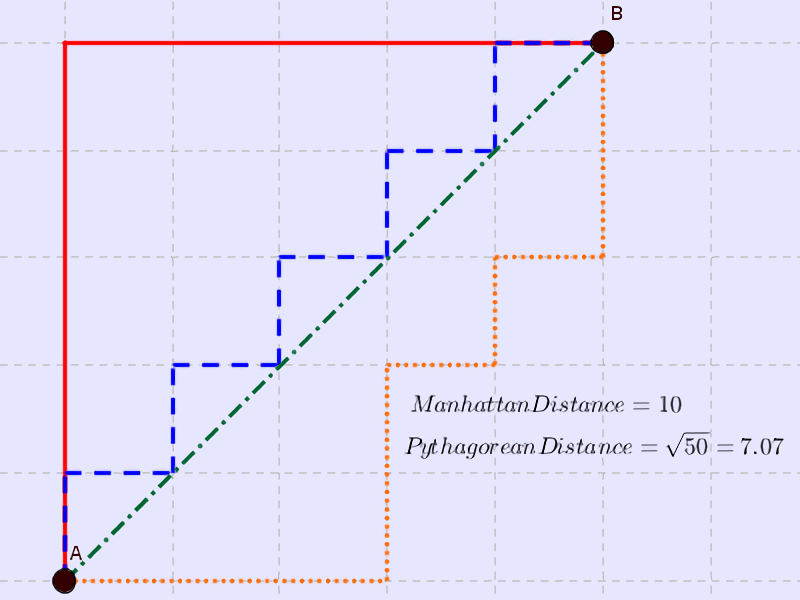
L'origine du nom de cette distance Manhattan (ou distance de taxi) vient de la structure en quadrillage régulier des rues du quartier de Manhattan (New York). C'est la distance entre deux points dans un environnement basé sur une grille (avec uniquement des mouvements horizontaux et verticaux). La distance de Manhattan est la simple somme des mouvements horizontaux et verticaux, alors que la distance diagonale ou "à vol d'oiseau" pourrait être calculé en appliquant le théorème de Pythagore.

Cette distance est idéale pour nos labyrinthes qui permettent 4 mouvements (haut, bas, gauche, droite). $$h(n) = |goal.x - root.x| + |goal.y - root.y|$$

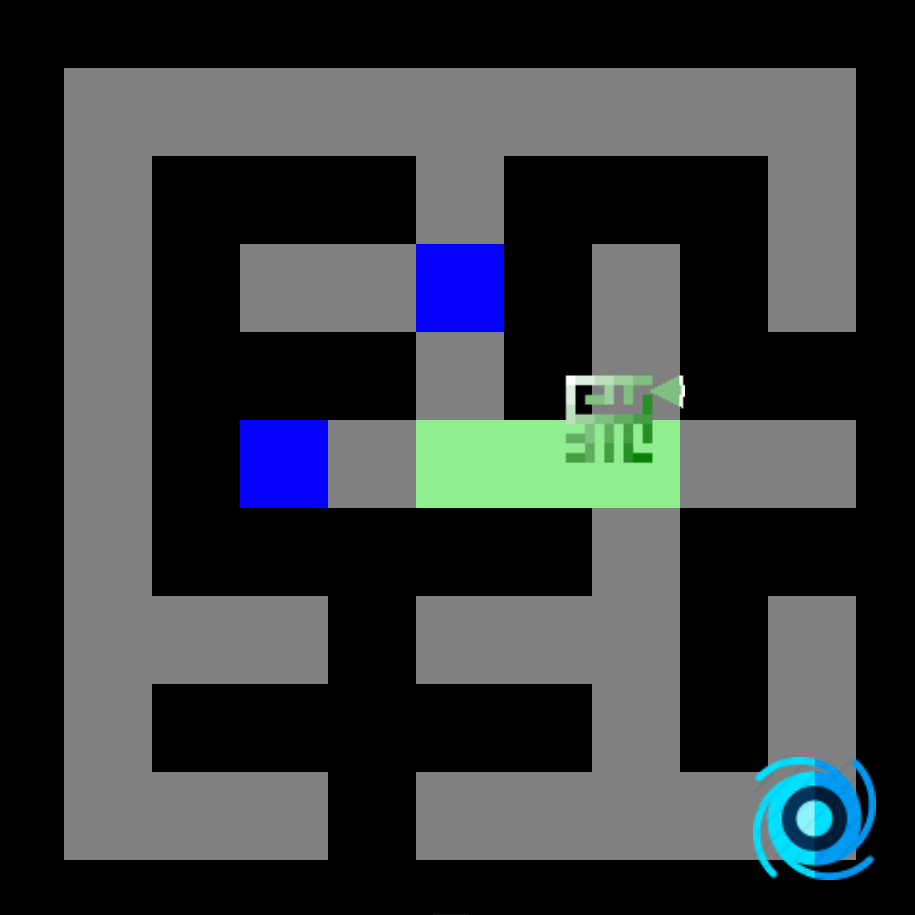
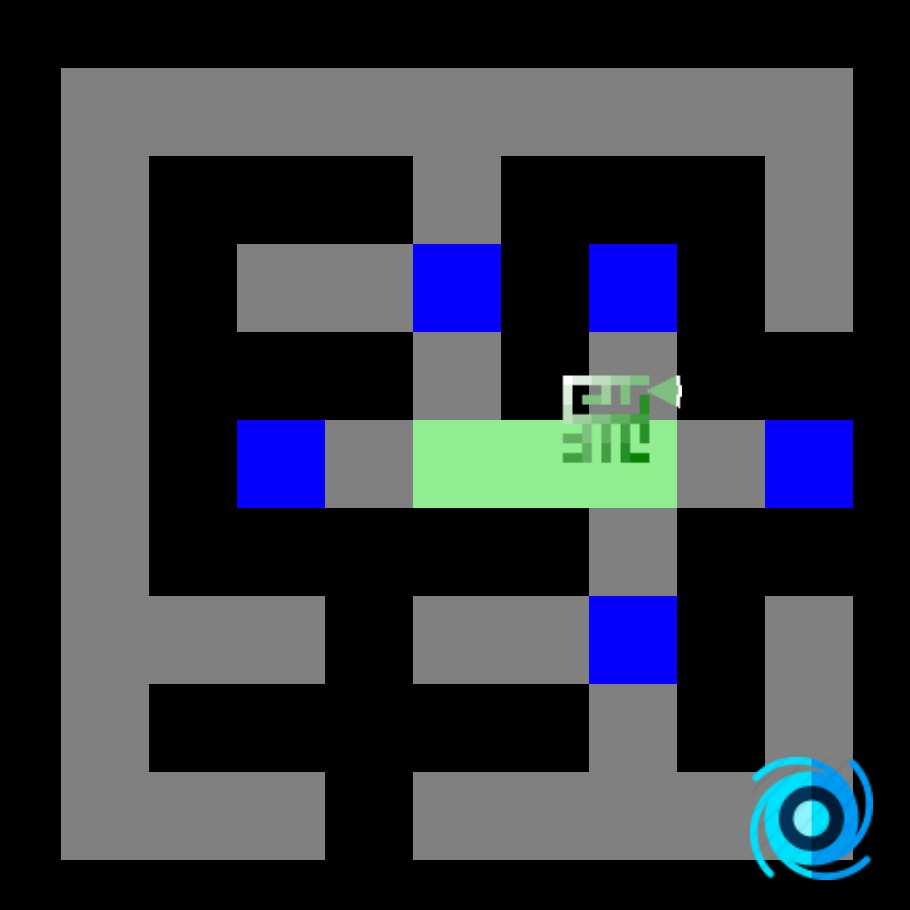
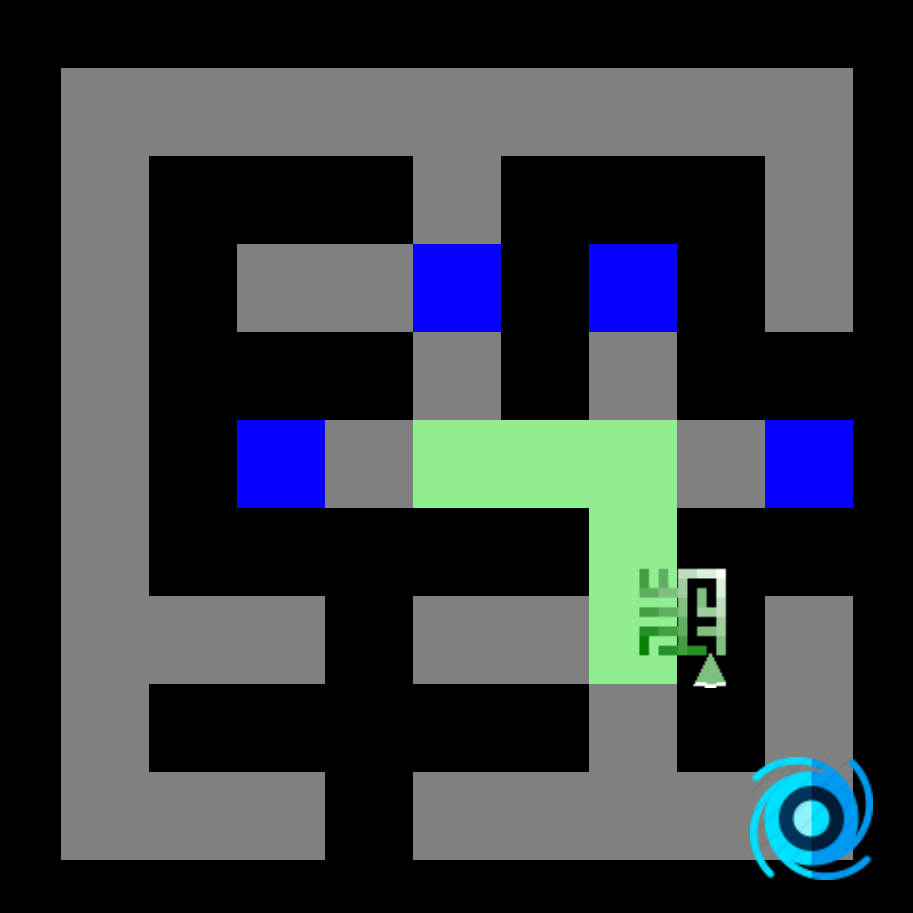
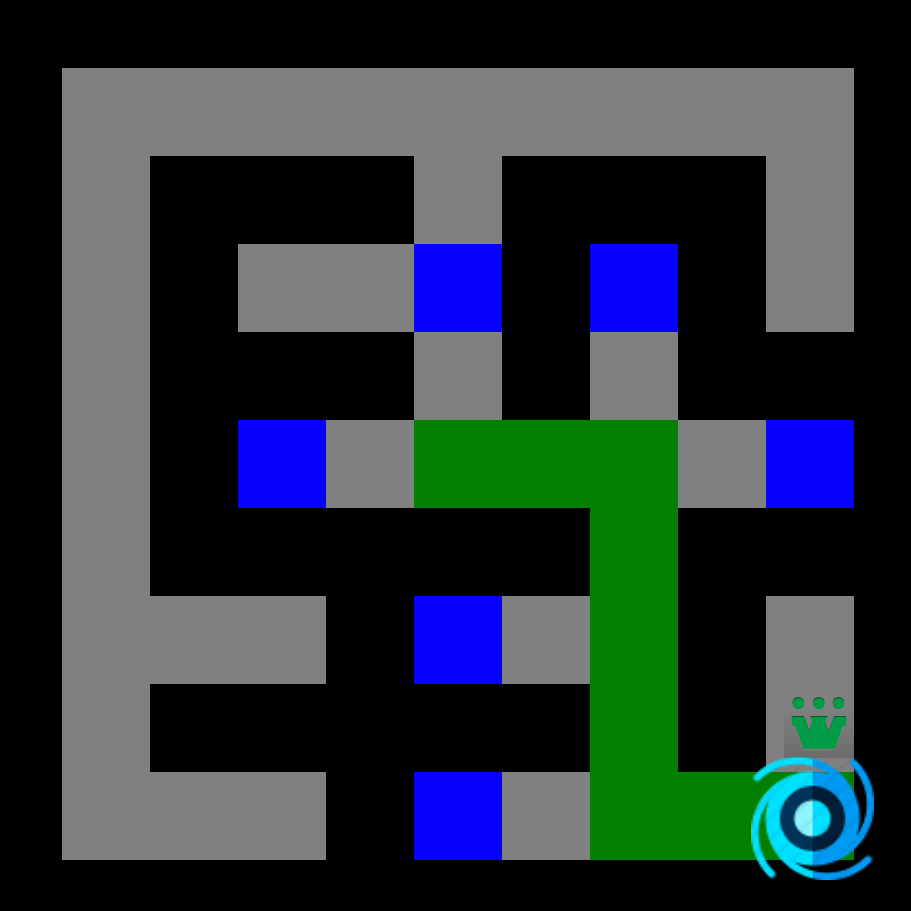
Voici les cartes de distance calculées (Manhattan, Dijkstra et A*) :

Carte des distances de Manhattan (à partir de la destination en bas à droite) : h(n)

Carte des distances de Dijkstra (à partir de la racine en haut à gauche) : g(n)

Carte de distances de A* : g(n) + h(n)

Nous pouvons renforcer l'heuristique de Manhattan en utilisant un facteur.
Par exemple avec: h(n) *= 2.

Étapes

Aussi simple que Dijkstra, le seul changement est la fonction de coût (nous ajoutons la distance de Manhattan)!

Code

AStar(Maze maze, Node start, Node end) {
    priority_queue queue();

    // Init all distances with infinity
    for (auto&& node : maze.nodes) {
      node.distance = Infinity;
      node.rootDistance = Infinity;

      // Note: we may reinforce the manhattan heuristic by using a factor.
      node.manhattanD = 2 * (Math.abs(end.x - node.x) + Math.abs(end.y - node.y));
    }

    // Distance to the root itself is zero
    start.rootDistance = 0;

    // Init queue with the root node
    queue.add(start, 0);

    // Iterate over the priority queue until it is empty.
    while (!queue.isEmpty()) {
      curNode = queue.dequeue();  // Fetch next closest node
      curNode.discovered = true;  // Mark as discovered

      // Iterate over unvisited neighbors
      for (auto&& neighbor : curNode.GetUnvisitedNeighbors())
      {
        // Update root minimal distance to neighbor including manhattan distance
        neighbor.rDistance =
          Math.min(neighbor.rootDistance, curNode.rootDistance + 1);
        const minDistance =
          Math.min(neighbor.distance, neighbor.rootDistance + neighbor.manhattanD);
        if (minDistance !== neighbor.distance) {
          neighbor.distance = minDistance;  // update mininmal distance
          neighbor.parent = curNode;        // update best parent

          // Change queue priority of the neighbor since it have became closer.
          if (queue.has(neighbor)) queue.setPriority(neighbor, minDistance);
        }

        // Add neighbor to the queue for further visiting.
        if (!queue.has(neighbor)) queue.add(neighbor, neighbor.distance);
      }
    }

  // Done ! At this point we just have to walk back from the end using the parent
  // If end does not have a parent, it means that it has not been found.
}

1. Voici notre plateau de jeu.

2. Calculons la distance des voisins et ajoutons-les à la file d'attente prioritaire.

3. Tous les nœuds ont la même distance racine. Cependant, nous sélectionnons celui de droite car il a une distance de Manhattan plus petite.

4. Encore une fois, nous calculons la distance des voisins et les ajoutons à la file d'attente prioritaire.

5. Encore une fois, notre heuristique favorise le chemin qui se rapproche de la cible.

6. C'est parti: destination trouvée en un clin d'oeil!