Notre plateau: un labyrinthe aléatoire de 30 x 20 généré à l'aide d'un algorithme de Prim.
Globo (notre mascotte verte au milieu) est le joueur et la capsule bleue est la sortie.

Trace laissée par le joueur utilisant l'algorithme de Dijkstra pour atteindre la sortie.

En comparaison, voici la trace laissée par une recherche en profondeur.

Enfin, celle laissée par une recherche en largeur.

Nous verrons pourquoi elle est similaire à celle de Dijkstra dans notre cas.

La recherche de chemins dans un réseau a pris de l'importance au début des années 50, notamment dans le contexte du routage. Il a fallu trouver de nouvelles solutions pour trouver les directions les plus courtes entre un endroit et une ou plusieurs destinations. En 1956, l'ingénieur logiciel néerlandais Edsger Wybe Dijkstra a créé le plus connu de ces algorithmes: Dijkstra.

L'algorithme de Dijkstra trouve le chemin le plus court d'un nœud de départ vers tous les autres nœuds (jusqu'à ce que l'objectif soit atteint). Dijkstra est l'un des algorithmes de parcours de graphes les plus utiles ; en outre, il peut facilement être modifié pour résoudre de nombreux autre problèmes.

Les algorithmes tels que la recherche en largeur et la recherche en profondeur explorent toutes les possibilités : ils parcourent tous les chemins possibles jusqu'à ce qu'ils atteignent la cible. Néanmoins, il peut ne pas être nécessaire d'examiner tous ces chemins; l'algorithme de Dijkstra optimise la traversée en utilisant une heuristique pour trouver les chemins optimaux.

Quelques utilisations courantes

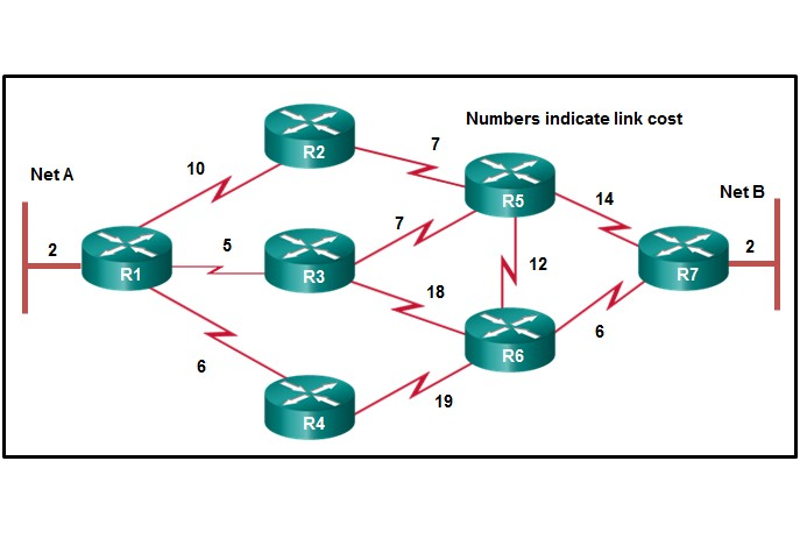
• Largement utilisé dans les protocoles de routage réseau.
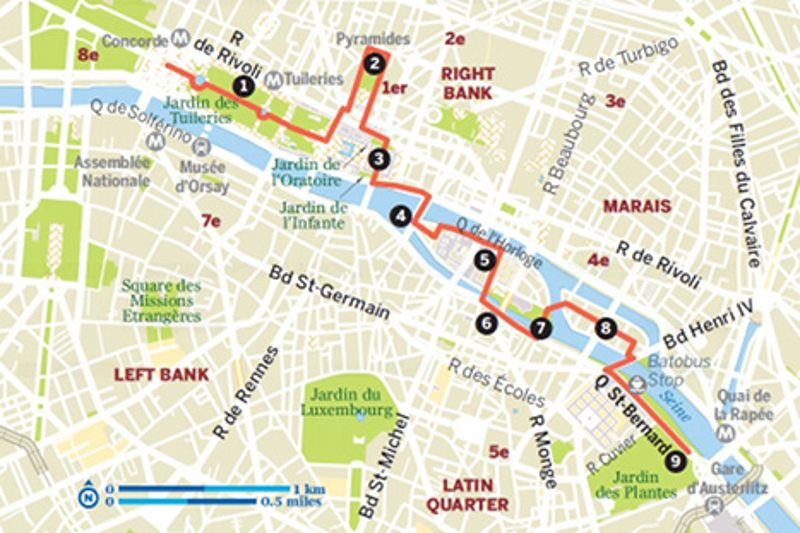
• Dans les services de cartographie numérique tels que Google Maps.
• En biologie avec les modèles de réseau dans la propagation des maladies infectieuses.
• Pour trouver l'agenda optimal des vols.
• Dans la planification de chemin pour le transport de robots mobiles...

Utilisé pour calculer une promenade romantique au bord de l'eau à Paris.

Utilisé pour trouver un routage réseau.

Utilisé dans des modèles tels que «simulation de maladies infectieuses aéroportées au niveau de la ville».

Utilisé pour trouver l'agenda optimal des vols.

Cet algorithme commence par un nœud racine et une file d'attente vide. À chaque étape, nous calculons la distance minimale entre la racine et chaque voisin non visité. Ensuite, nous les ajoutons à la file d'attente; celui qui a la distance la plus faible dans la queue est le suivant qui sera extrait. Ce processus se répète jusqu'à ce qu'un chemin vers la destination soit trouvé.

Étant donné que les nœuds les plus proches sont examinés en premier, la première fois que la destination est trouvée, le chemin qui y mène est le plus court.

Minimiser la distance au nœud racine est notre heuristique ici.

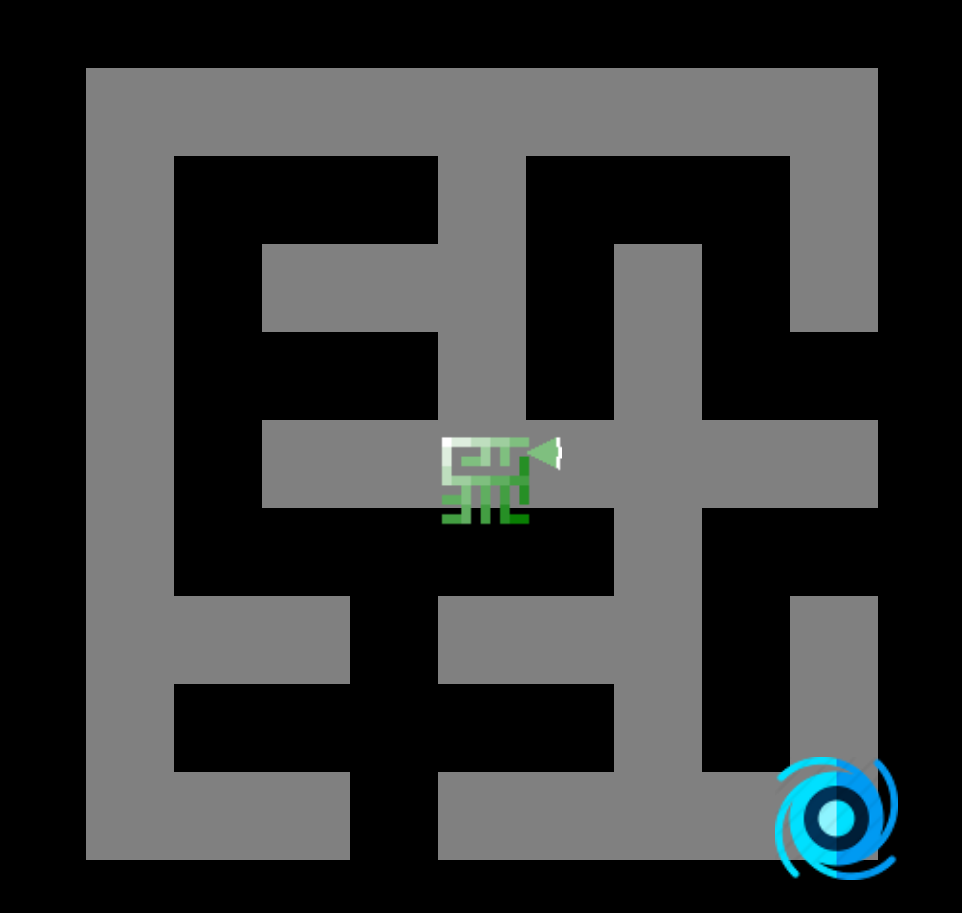
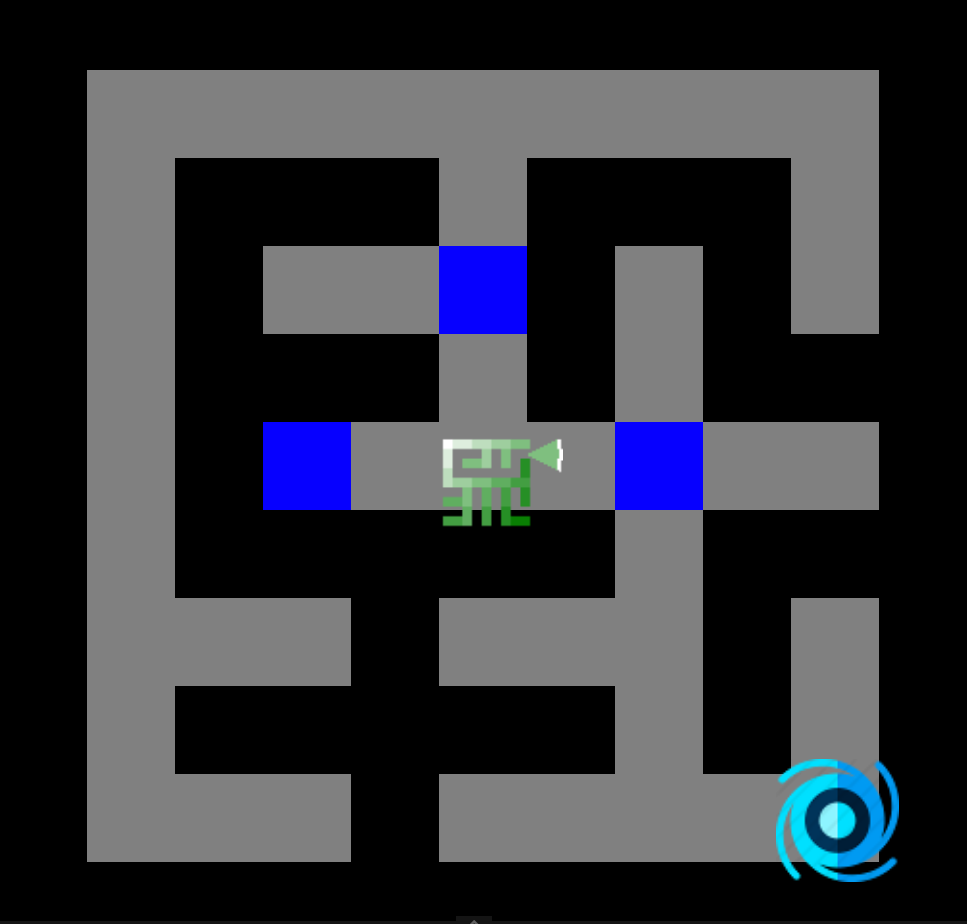
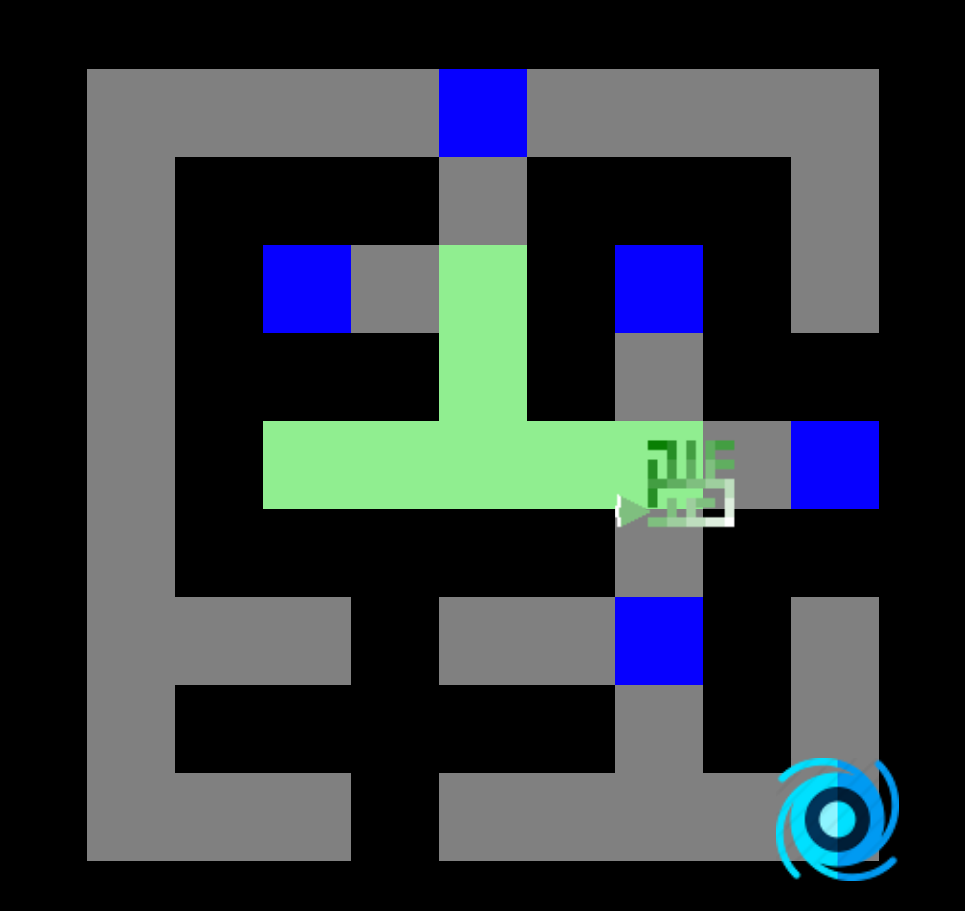
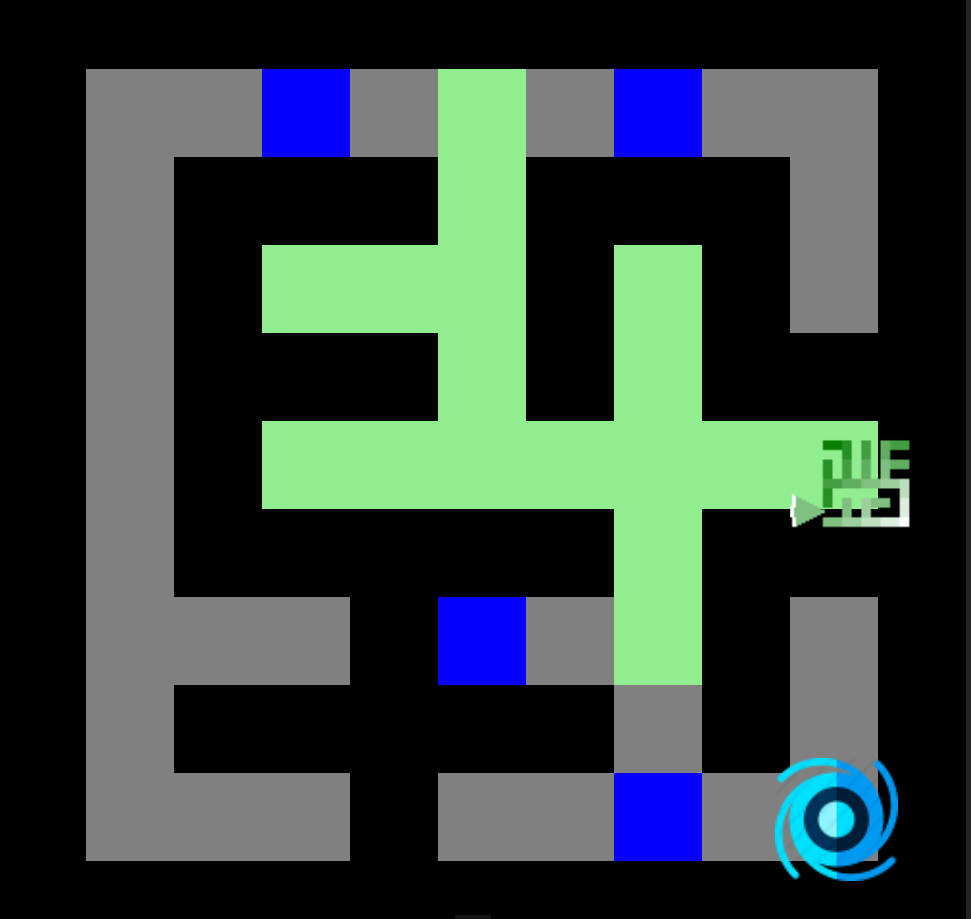
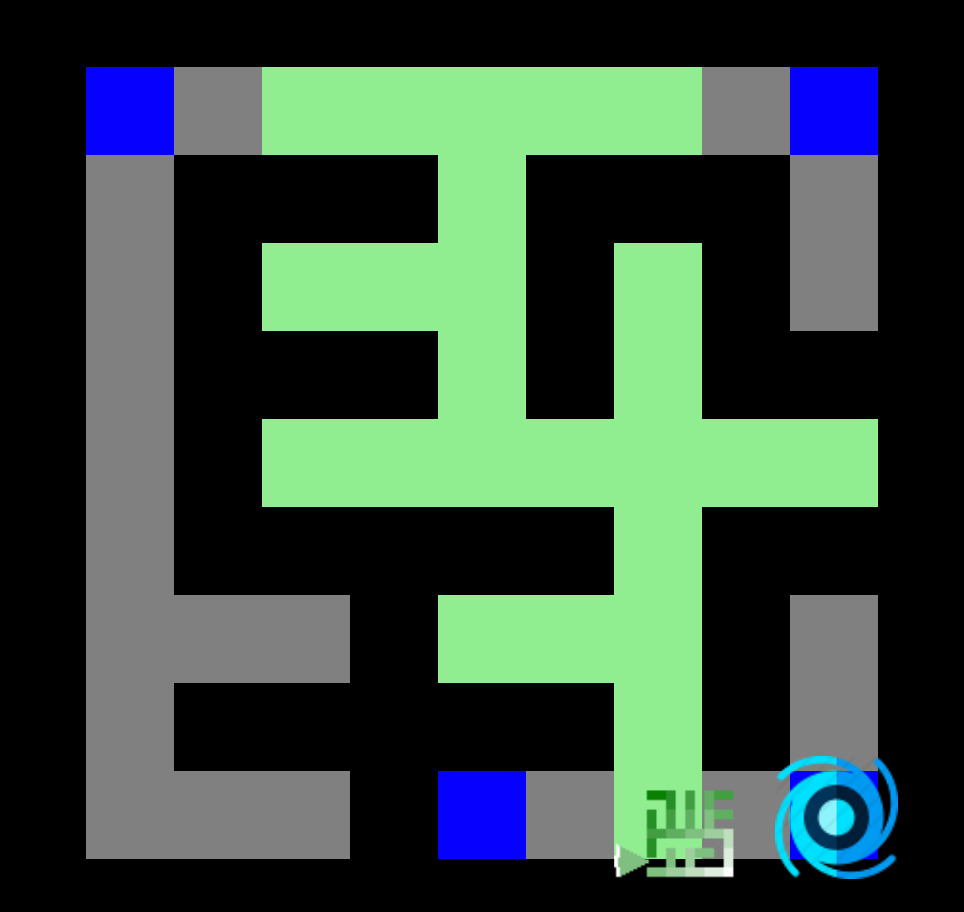
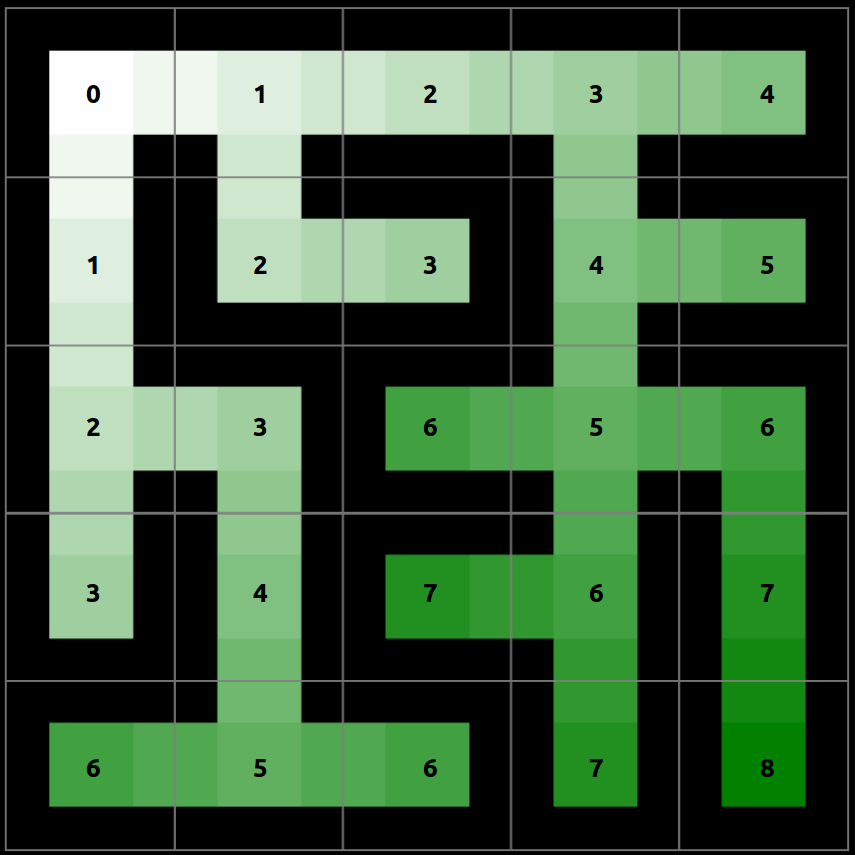
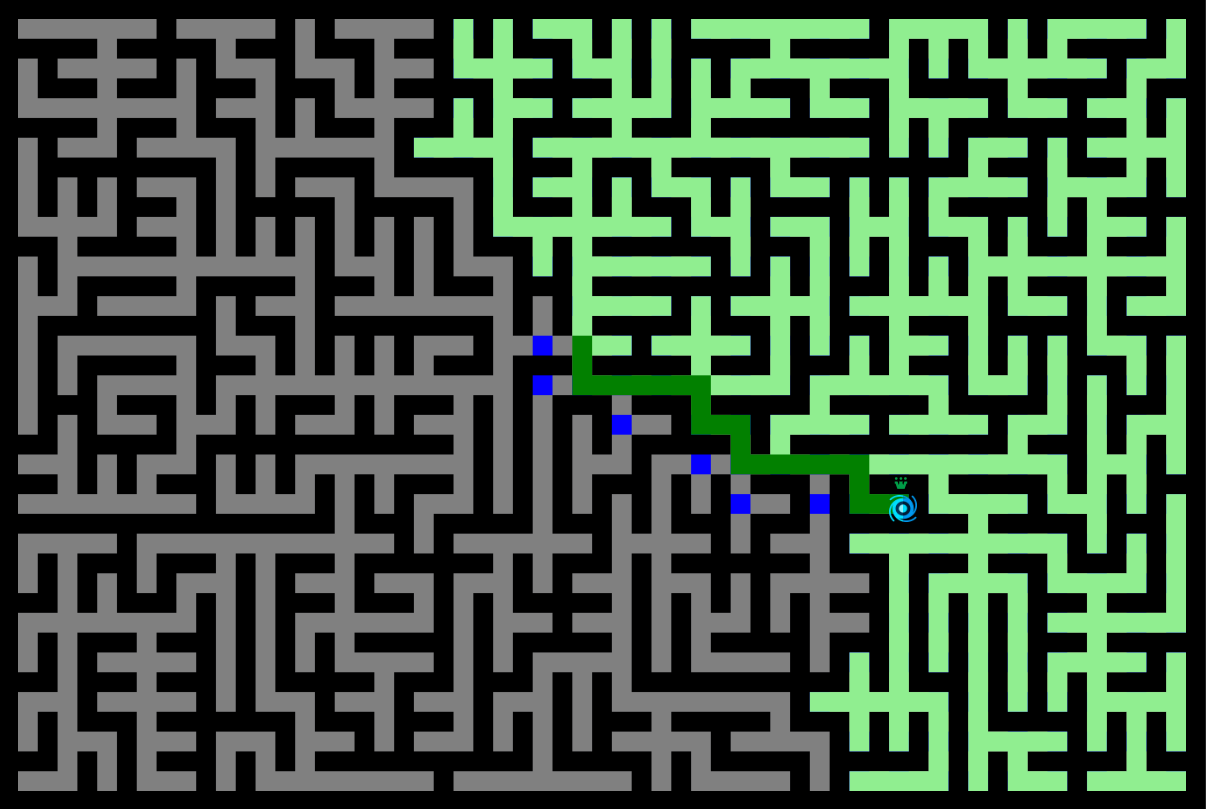
Voici la carte des distances calculée pour un labyrinthe à partir du coin supérieur gauche (racine). Nous pouvons remarquer que chaque connexion entre deux nœuds adjacents a un coût distance de 1.

Étapes

Prenons un nœud racine et notons D la distance d'un nœud à cette racine. L'algorithme de Dijkstra attribuera des valeurs de distance initiales et les améliorera pas à pas.

• 1. Assigner toutes les distances D à l'infini sauf pour le nœud racine dont la distance est 0.
• 2. Marquer le nœud actuel comme visité et mettre à jour D pour tous ses voisins non visités avec la distance la plus courte.
  Remarque: nous pouvons arrêter l'algorithme ici si nous avons atteint le nœud cible.
• 3. Ajouter à la file d'attente les nœuds non visités et reprendre à l'étape 2.

Oui, l'un des algorithmes les plus utiles et les plus utilisés est aussi simple que cela !

Comme nous l'avons vu : en calculant et en actualisant continuellement la distance la plus courte, l'algorithme compile le chemin le plus court vers la destination. Un élément clé de cette approche consiste à maintenir une ligne ordonnée de nœuds à visiter en priorité; pour coder cette partie de l'algorithme, nous utiliserons une file d'attente prioritaire ou 'priority queue' (une file d'attente régulière avec la possibilité de fixer des priorités).

Pour l'algorithme de Dijkstra, il est toujours recommandé d'utiliser une file d'attente prioritaire (priority queue or heap) car les opérations requises (extraire la clé minimum et diminuer) est la spécialité de cette structure de données. Ici, la priorité est définie par D (la distance entre un nœud et la racine). Des priorités plus élevées sont données pour les nœuds avec une distance D plus faible.

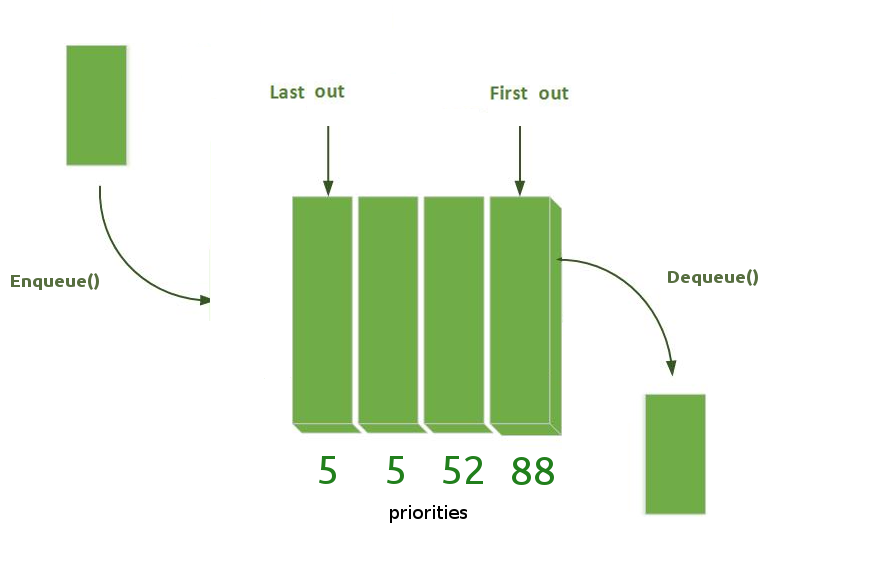
Nous pouvons le voir comme une file d'attente d'attraction avec certaines personnes ayant un accès vers différents points de contrôle. Une file d'attente prioritaire doit avoir les méthodes suivantes:

// Add new element at the end of the queue
void enqueue(const T& data, const int priority);

// Remove element from the beginning of the queue
void dequeue();

// Change the priority of the element in the queue.
void changePriority(const T& item, const int priority);

Maintenant que nous savons tout ce que nous devons savoir, voici l'implémentation (l'explication visuelle suit):

Code

Dijkstra(Maze maze, Node start, Node end) {
    priority_queue queue();

    // Init all distances with infinity
    for (auto&& node : maze.nodes) node.distance = Infinity;

    // Distance to the root itself is zero
    start.distance = 0;

    // Init queue with the root node
    queue.add(start, 0);

    // Iterate over the priority queue until it is empty.
    while (!queue.isEmpty()) {
      curNode = queue.dequeue();  // Fetch next closest node
      curNode.discovered = true;  // Mark as discovered

      // Iterate over unvisited neighbors
      for (auto&& neighbor : curNode.GetUnvisitedNeighbors())
      {
        // Update minimal distance to neighbor
        // Note: distance between to adjacent node is constant and equal 1 in our grid
        const minDistance = Math.min(neighbor.distance, curNode.distance + 1);
        if (minDistance !== neighbor.distance) {
          neighbor.distance = minDistance;  // update mininmal distance
          neighbor.parent = curNode;        // update best parent

          // Change queue priority of the neighbor since it have became closer.
          if (queue.has(neighbor)) queue.setPriority(neighbor, minDistance);
        }

        // Add neighbor to the queue for further visiting.
        if (!queue.has(neighbor)) queue.add(neighbor, neighbor.distance);
      }
    }

  // Done ! At this point we just have to walk back from the end using the parent
  // If end does not have a parent, it means that it has not been found.
}

NOTE
L'algorithme de Dijkstra ne prend pas en charge les distances négatives. L'algorithme suppose que l'ajout d'une relation à un chemin ne peut jamais raccourcir un chemin, un invariant qui serait violé avec des distances négatives.

1. Voici notre plateau de jeu.

2. Nous examinons la distance des voisins non visités et les ajountons à la file d'attente. Ce sont les nœuds les plus proches de la racine (premier cercle, distance = 1).

3. Chacun des nœuds les plus proches sera examiné en premier tout en ajoutant leurs voisins les plus proches à la file d'attente. Il s'agit du deuxième cercle (distance = 2) de la racine (le plus proche du plus proche).

4. Voici le troisième.

5. Maintenant le quatrième.

6. Et voila: destination trouvée!

Les nœuds sont explorés de manière uniforme dans toutes les directions, apparaissant comme une onde circulaire (similairement à la recherche en largeur). Cela est due à notre utilisation d'un coût constant de 1 pour toutes les connexions entre deux nœuds adjacents.

L'utilisation d'une file d'attente prioritaire au lieu d'une file d'attente régulière modifie la façon dont la frontière s'étend. Les lignes de contour (basées sur les distances) sont une façon de voir cela:

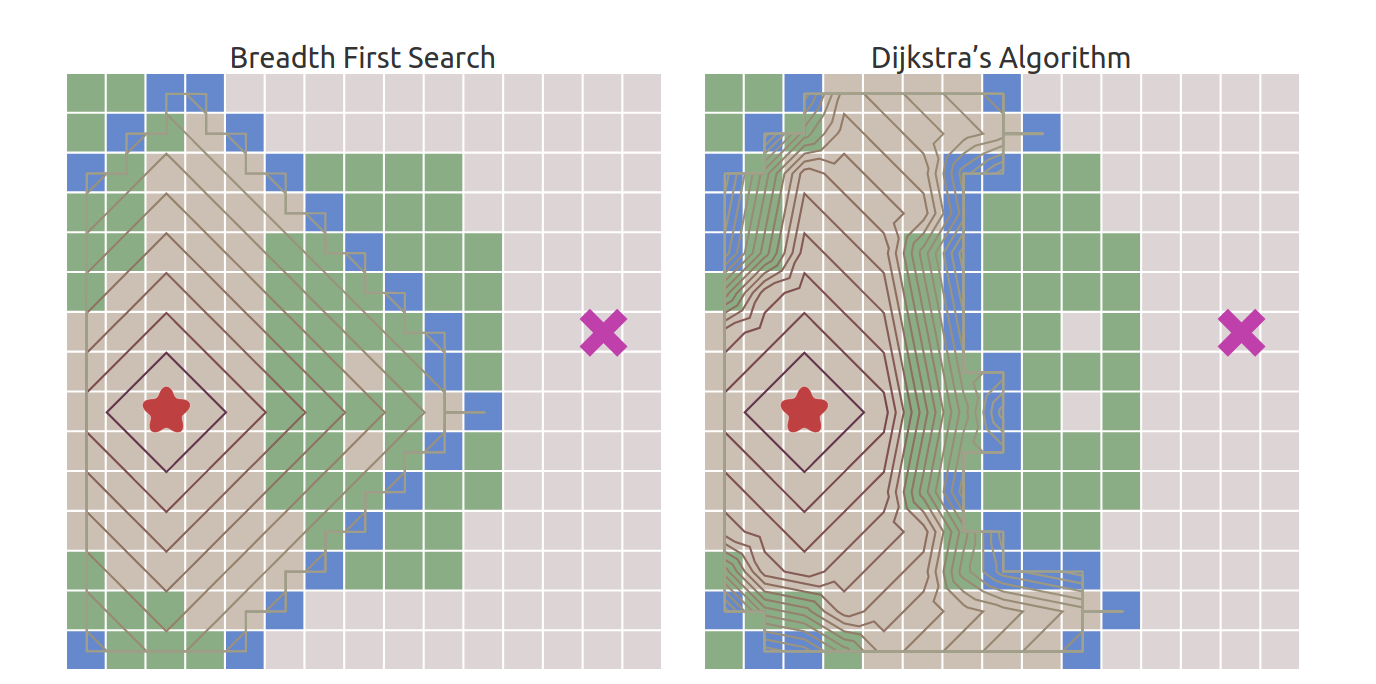
La frontière s'étend plus lentement à travers les forêts (source: redblobgames).