Notre terrain de jeu : un labyrinthe aléatoire de 30 x 20 généré avec un algorithme de Prim.
Globo (le carré vert au milieu) est le joueur et la capsule bleue est la sortie.

Trace laissée par une recherche en profondeur dans notre labyrinthe.

En comparaison, voici la trace laissée par une recherche en largeur.

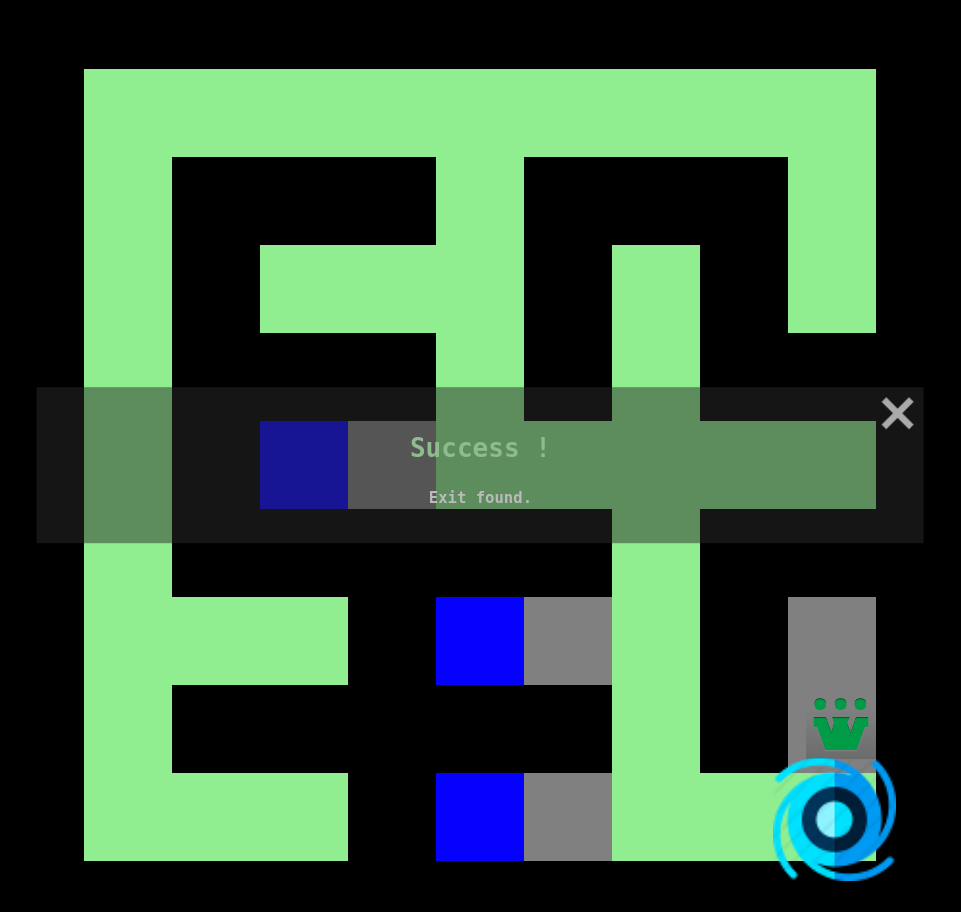
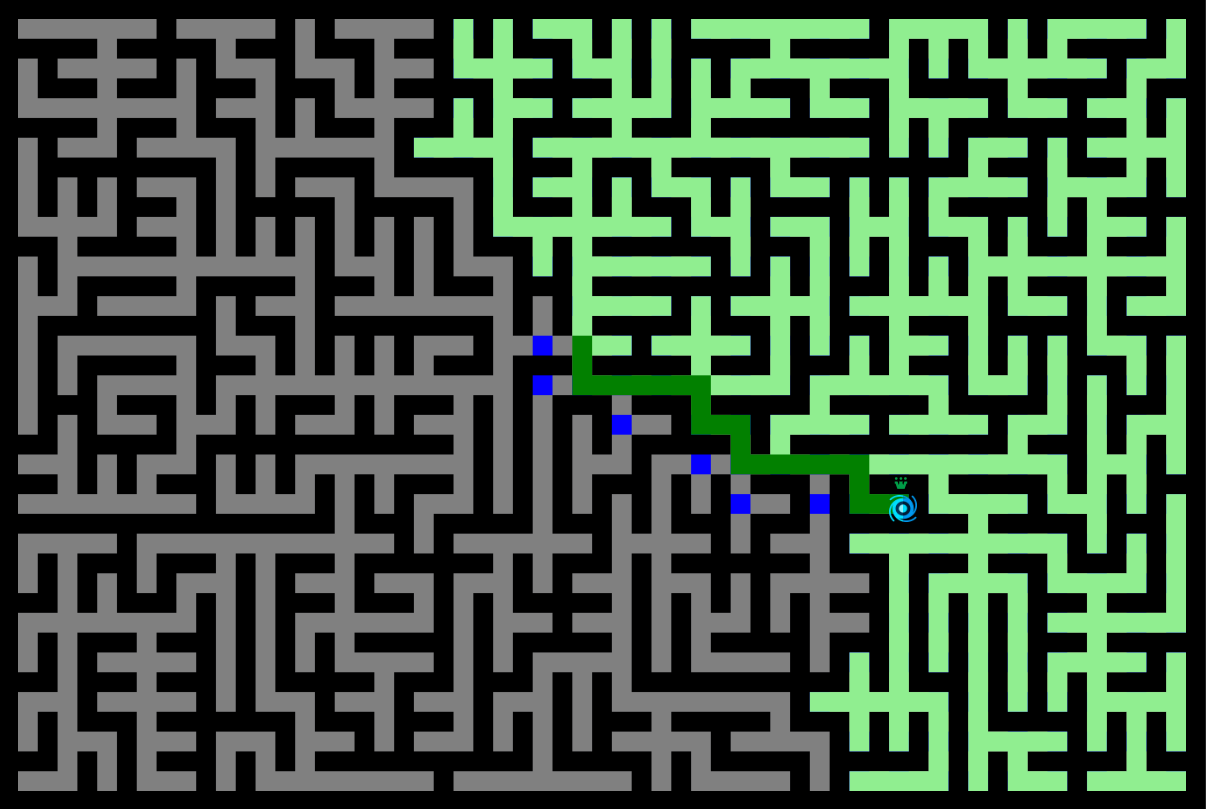
La recherche en profondeur (DFS) est l’autre algorithme fondamental de parcours de graphe; La première, la recherche en largeur (BFS), est son antonyme. Aussi utile que le BFS, le DFS peut être utilisé pour générer un ordre topologique, générer des labyrinthes (cf. générateurs de labyrinthe DFS), pour traverser les arbres dans un ordre spécifique, pour construire des arbres de décisions, pour découvrir un chemin de solution avec des choix hiérarchiques, pour détecter un cycle dans un graphe...

Cependant, veuillez d'abord noter que le DFS ne garantit pas le chemin le plus court.
De ce fait, ce n’est pas un très bon algorithme si le seul but est de une recherche simple de chemin entre deux noeuds.

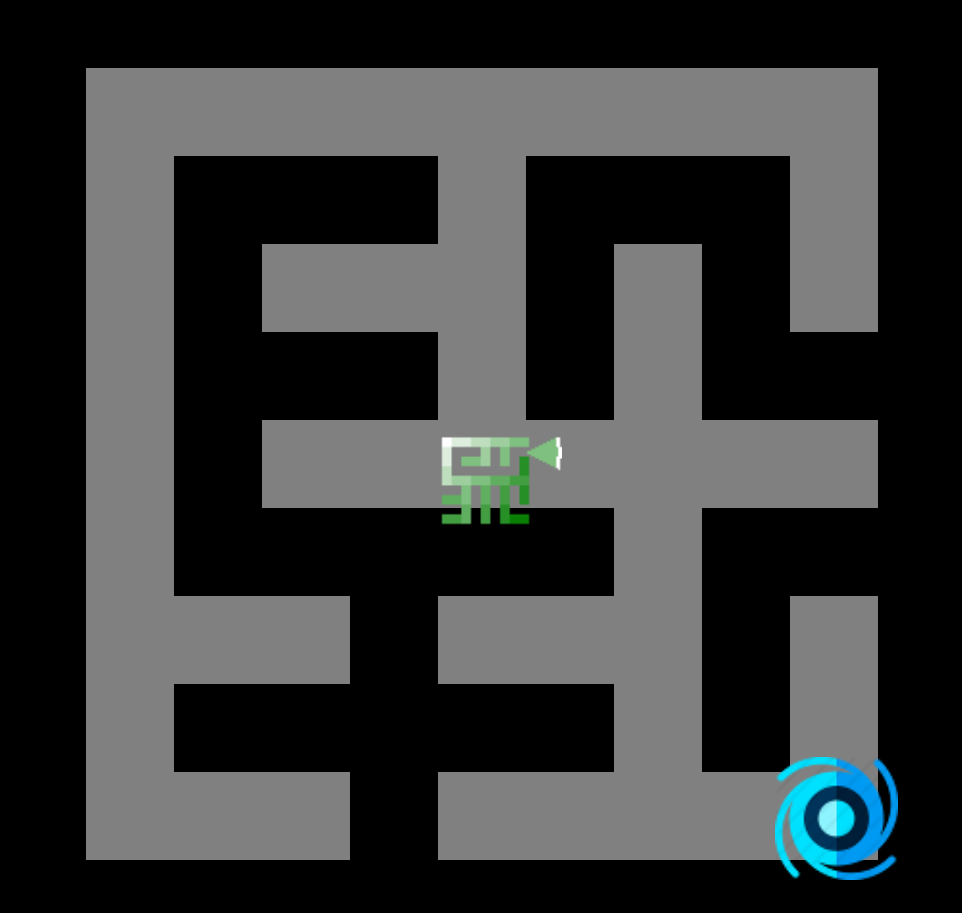
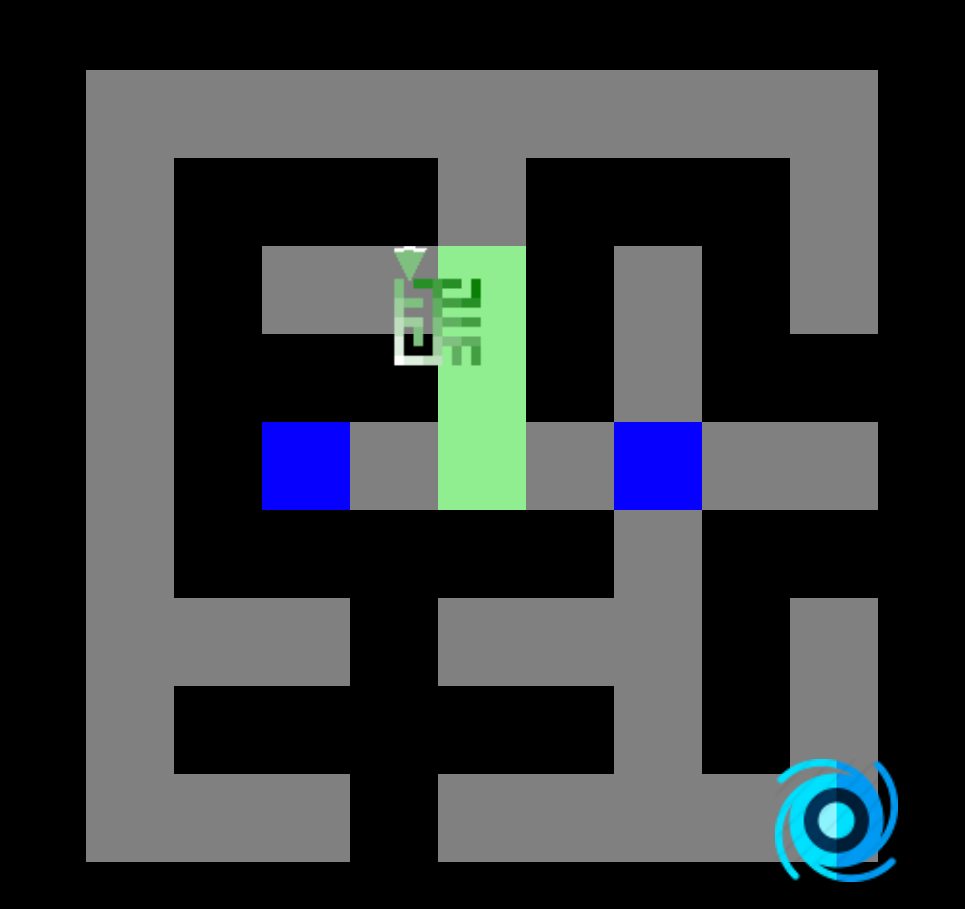
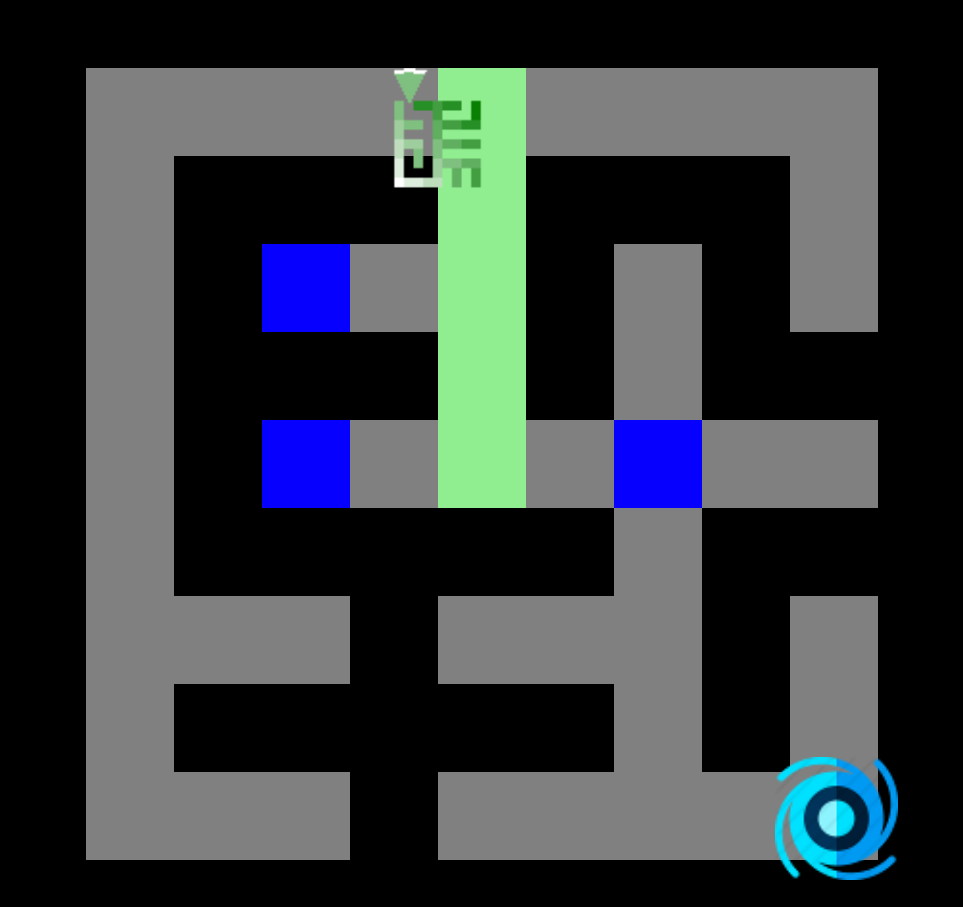
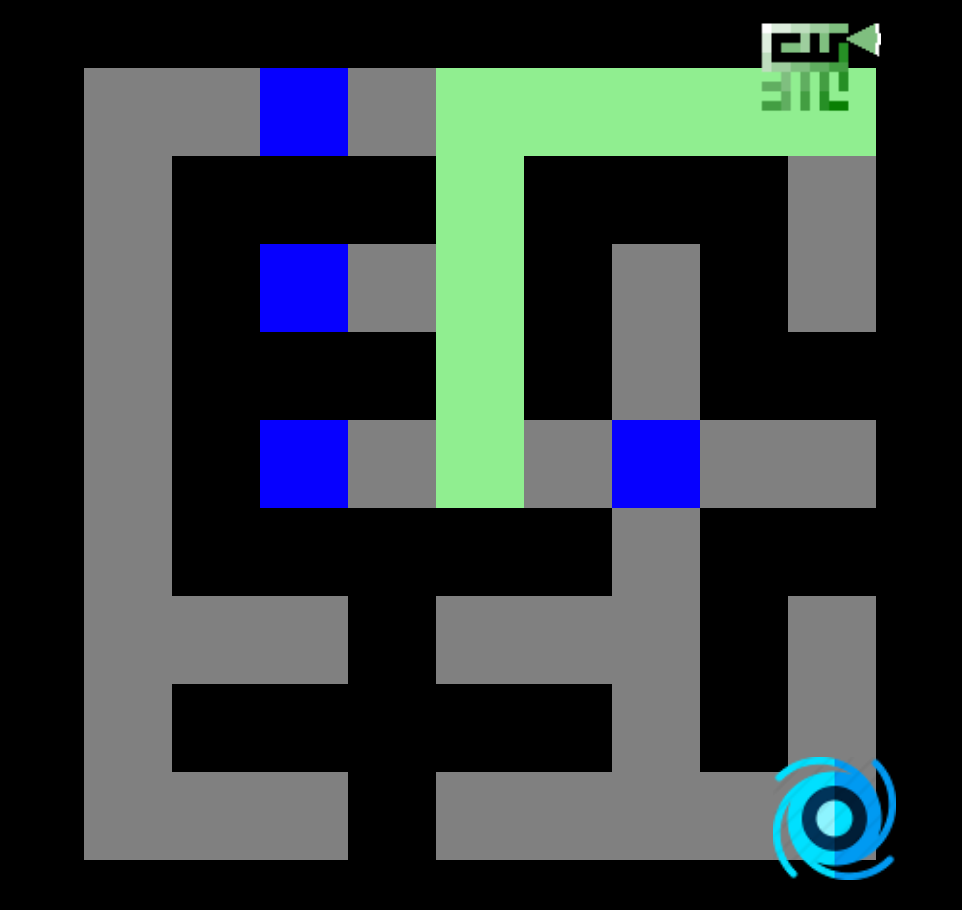
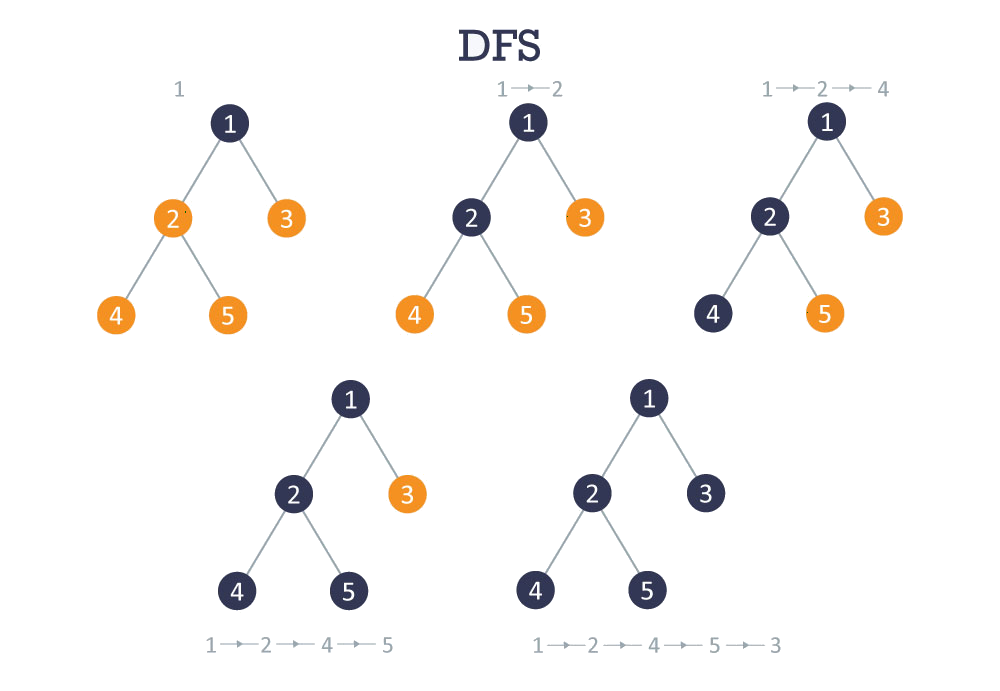
La recherche en profondeur taverse en explorant chaque chemin le plus loin possible avant de devoir revenir en arrière. C’est la raison pour laquelle vous pouvez également trouver cet algorithme sous le nom de Backtracking (Retour en arrière). De plus, cette propriété permet de mettre en oeuvre l'algorithme succinctement à la fois sous forme itérative et récursive. Si nous considérons une arborescence (qui est un graphe simplifié), la DFS procédera comme suit:

Étapes

• Ajouter le noeud de départ dans la pile et marquez comme visité.
• Tant qu'il y a un noeud dans la pile:
• 1. Prendre le noeud au dessus de la pile.
• 2. Ajouter sur la pile tous les voisins disponibles dans l'ordre, noter le parent et marquer comme visité.
  (nous avons choisi pour la visualisation Nord, Est, Sud, Ouest comme ordre)
• Fini : obtenir le chemin en utilisant le parent depuis la fin.

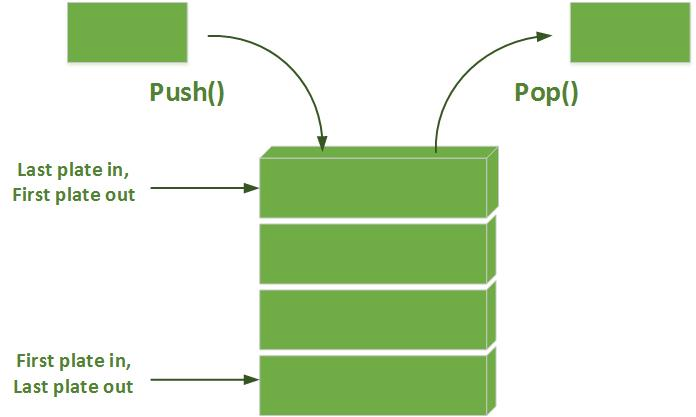
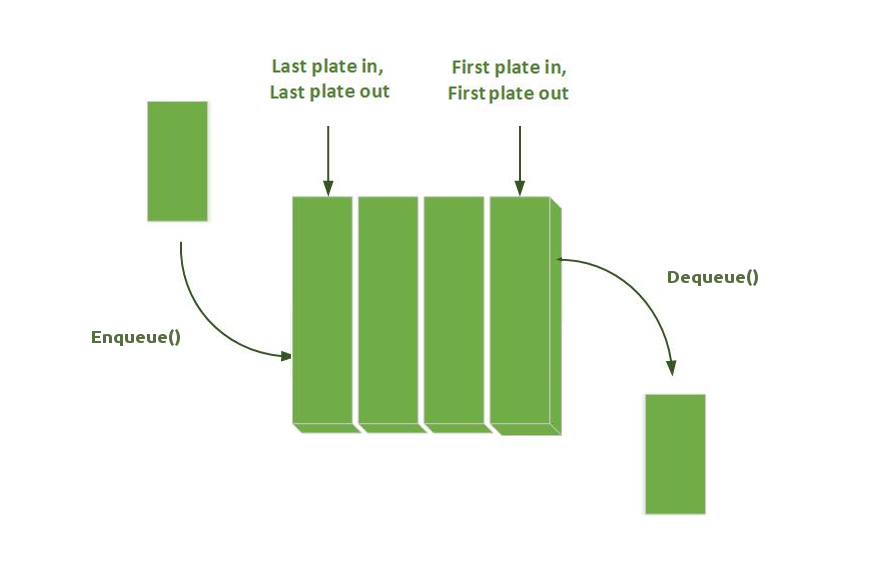
DFS utilise la stratégie opposée à celle de la recherche en largeur qui explore cercle par cercle. Pourtant, les deux algorithmes ont les mêmes lignes de code; la seule différence réside dans la structure de données utilisée:

DFS utilise une Stack - Pile (LIFO)	BFS utilise une Queue (FIFO)

Code

DFS(Maze maze, Node start, Node end)
{
  // Put the start node in the stack
  start.visite = true;
  Stack stack(start);

  // While there is node to be handled in the stack
  while (!stack.empty())
  {
    // Handle the node on the top of the stack and retrieve its unvisited neighbors
    Node curNode = stack.pop();

    // Terminate if the goal is reached
    if (curNode == end)
      break;

    // Take unvisited neighbors in order (eg. Noth, East, South, West),
    // set its parent, mark as visited, and add to the stack
    auto neighbors = curNode.GetUnvisitedNeighbors();
    for (auto i = 0; i < neighbors.size(); ++i)
    {
      neighbors[i].visite = true;
      neighbors[i].parent = curNode;
      stack.push(neighbors[i]);
    }
  }

  // Done ! At this point we just have to walk back from the end using the parent
  // If end does not have a parent, it means that it has not been found.
} 

Version Récursive

La récursivité de l’algorithme DFS provient du fait que nous ajoutons les contextes sur la call stack tant que nous n’avons pas atteint une impasse. Lorsque nous revenons en arrière, nous supprimons le context en haut de la pile d’appels. Plus que des mots, le code parle de lui-même ^^

bool Recursive_DFS(Maze maze, Node start, Node end)
{
  // Terminate if the goal is reached
  if (start == end)
    return true;

  // Visite current node
  start.visite = true;

  // Take unvisited neighbors in order (eg. North, East, South, West),
  auto neighbors = start.GetUnvisitedNeighbors();
  for (auto i = 0; i < neighbors.size(); ++i)
  {
    neighbors[i].parent = start;

    // Recurse and Terminate if the goal is reached
    if (Recursive_DFS(maze, neighbors[i], end)) return true;
  }

  return false;
} 

1. Voici notre petit plateau de jeu.

2. Ajoutez tous les voisins non visités à la pile, ils seront traités avec la dernière direction toujours au dessus de la pile (Nord dans cet exemple).

3. Le joueur se dirige alors toujours vers le nord aussi longtemps qu'il le peut.

4. Une fois qu'il ne peut pas plus au nord, il ira vers l'Est (tant qu'aucun chemin ne s'ouvre au nord).

5. Lorsqu'il est bloqué, il effectue un retour en arrière et relance l'exploration de la prochaine branche disponible.

6. Après quelques itérations : sortie trouvée!