Our board : a random 30x20 maze generated using a Prim's algorithm.
Globo (the green square in the middle) is the player and the blue capsule is the goal.

Trace let by the player using a Depth First Search pathfinding algorithm to reach the goal.

Here is, to be compared, the trace let by the player using a Breadth First Search (BFS) pathfinding algorithm to reach the goal.

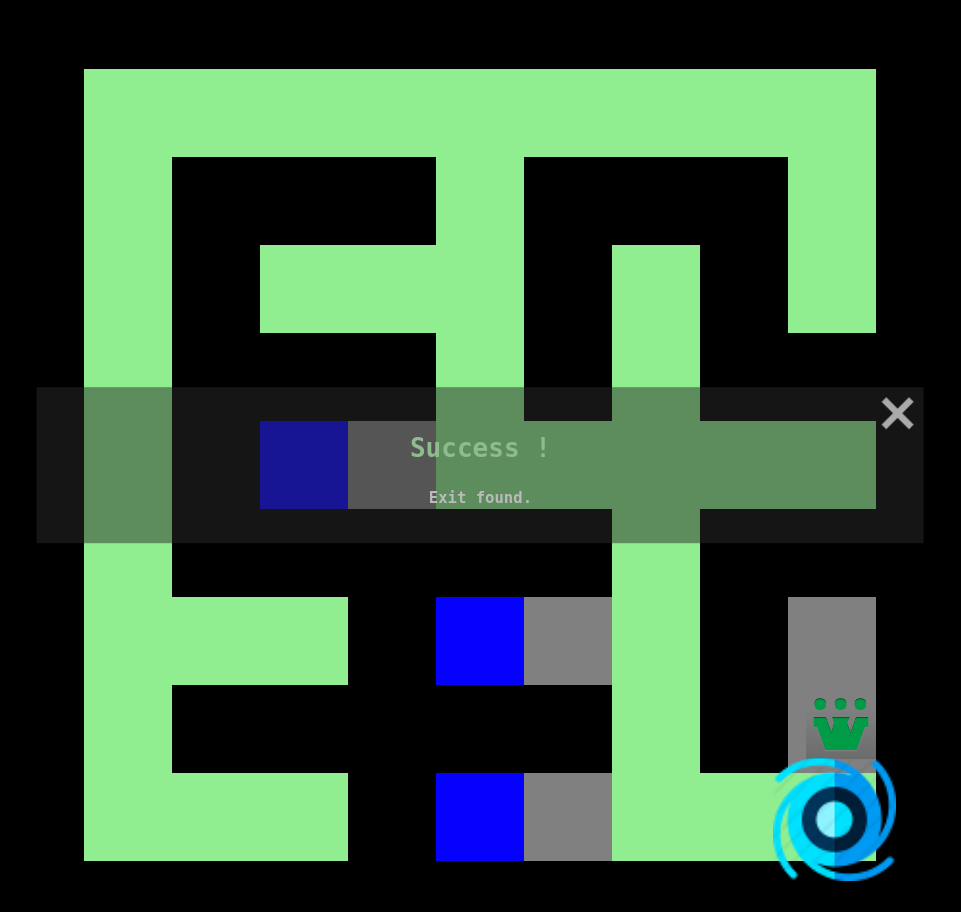
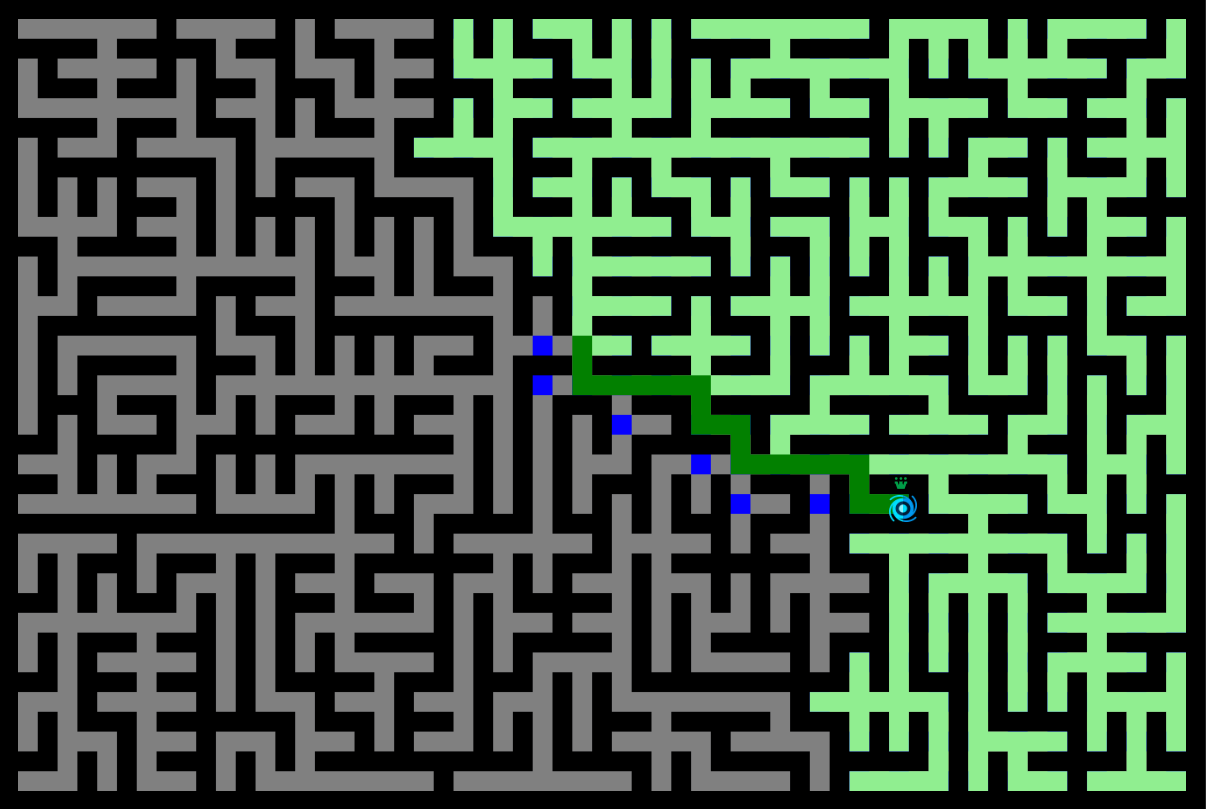
Depth First Search (DFS) is the other fundamental graph traversal algorithm; Breadth First Search (BFS) is the other one. As useful as the BFS, the DFS can be used to generate a topological ordering, to generate mazes (cf. DFS maze generators), to traverse trees in specific order, to build decision trees, to discover a solution path with hierarchical choices, to detect a cycle in a graph...

However, please first note that the DFS does not guarantee the shortest path.
Then, this is not a very good algorithm if the unique purpose is to do a simple pathfinding.

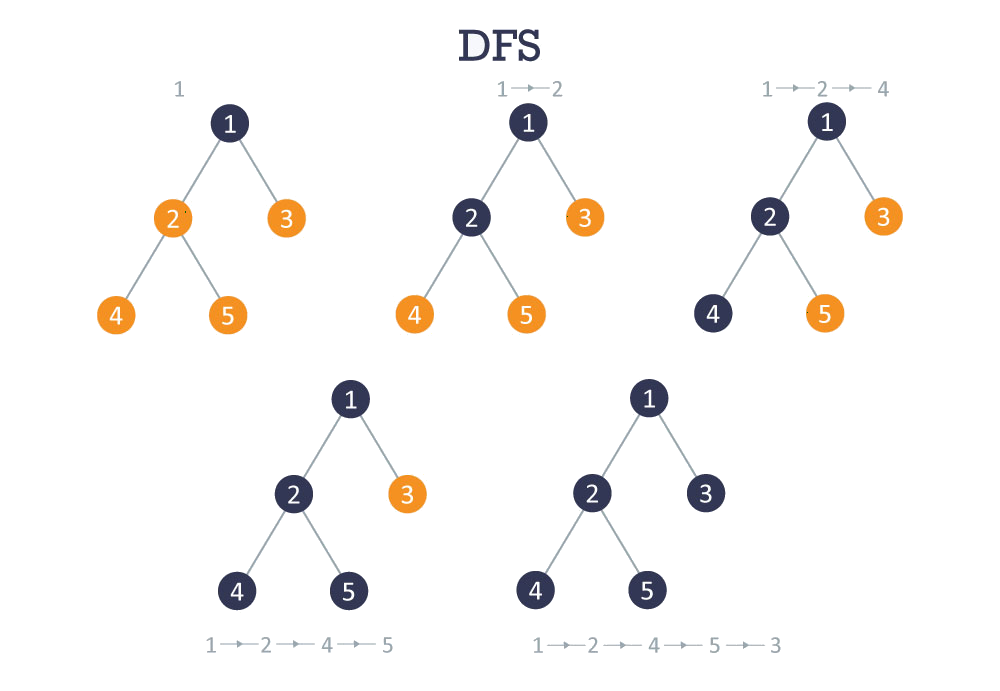
Depth First Search Traverses by exploring as far as possible down each path before going back. It is the reason why you may also find this algorithm under the name of Backtracking. Furthermore, This property allows the algorithm to be implemented succinctly in both iterative and recursive forms. If we consider a tree (which is a simplified graph), the DFS will proceed as follows:

Steps

• Add the start node in the stack and mark as visited.
• While there is a node waiting in the stack:
• 1. Take the node at the top of the stack.
• 2. Add on the stack all available neighbors in order, note the parent and mark as visited
  (we chose for the visualization North, East, South, West as order)
• Done: backtrack from goal to start using parent link in order to get the path.

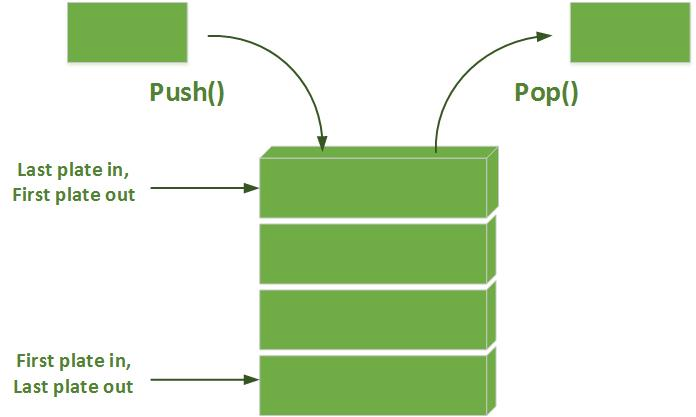
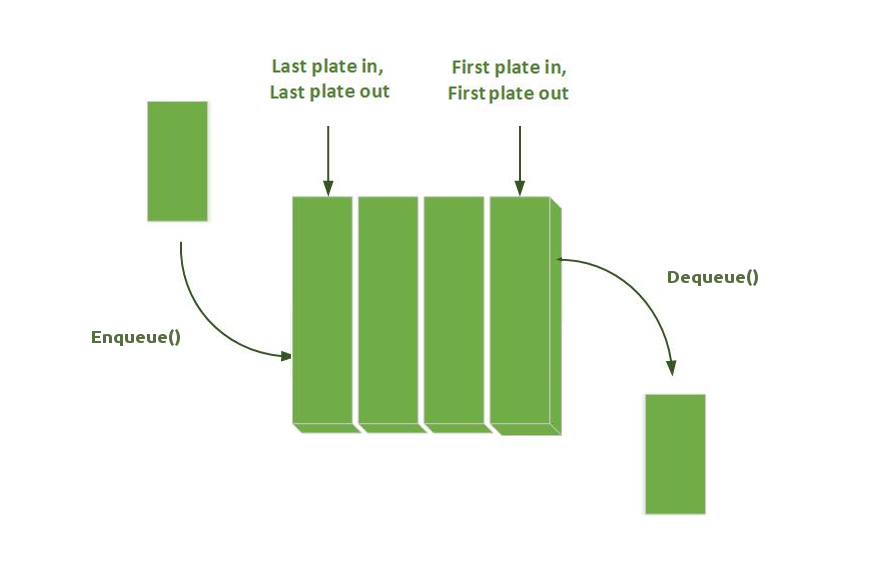
DFS uses the opposite strategy as breadth-first search (BFS), which instead explores the node circle by circle. Still, both algorithms have the same lines of code; the only difference is the data structure used:

DFS use a Stack (LIFO)	BFS use a Queue (FIFO)

Code

DFS(Maze maze, Node start, Node end)
{
  // Put the start node in the stack
  start.visite = true;
  Stack stack(start);

  // While there is node to be handled in the stack
  while (!stack.empty())
  {
    // Handle the node on the top of the stack and retrieve its unvisited neighbors
    Node curNode = stack.pop();

    // Terminate if the goal is reached
    if (curNode == end)
      break;

    // Take unvisited neighbors in order (eg. Noth, East, South, West),
    // set its parent, mark as visited, and add to the stack
    auto neighbors = curNode.GetUnvisitedNeighbors();
    for (auto i = 0; i < neighbors.size(); ++i)
    {
      neighbors[i].visite = true;
      neighbors[i].parent = curNode;
      stack.push(neighbors[i]);
    }
  }

  // Done ! At this point we just have to walk back from the end using the parent
  // If end does not have a parent, it means that it has not been found.
} 

Recursive version

The recursion of the DFS algorithm stems from the fact that we don’t actually finish checking a “parent” node until we reach a dead end, and inevitably pop off one of the “parent” node’s children from the top of the call stack. More than words, the code talks for itself ^^

bool Recursive_DFS(Maze maze, Node start, Node end)
{
  // Terminate if the goal is reached
  if (start == end)
    return true;

  // Visite current node
  start.visite = true;

  // Take unvisited neighbors in order (eg. North, East, South, West),
  auto neighbors = start.GetUnvisitedNeighbors();
  for (auto i = 0; i < neighbors.size(); ++i)
  {
    neighbors[i].parent = start;

    // Recurse and Terminate if the goal is reached
    if (Recursive_DFS(maze, neighbors[i], end)) return true;
  }

  return false;
} 

1. Here is our board.

2. Add all unvisited neighbors to the stack, they will be processed with the last direction always on top (North in this example).

3. The player is then always going north as long as he can.

4. Once he can't go north, he will keep on going East (as long as no path opens to north).

5. When stuck, it backtracks and restarts the exploration of the next available branch.

6. After few iterations : exit found!