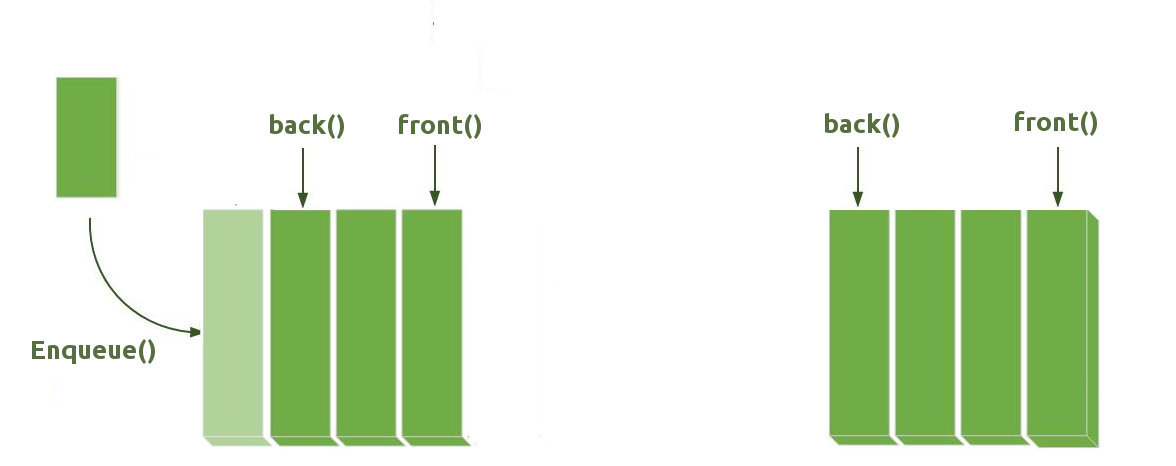
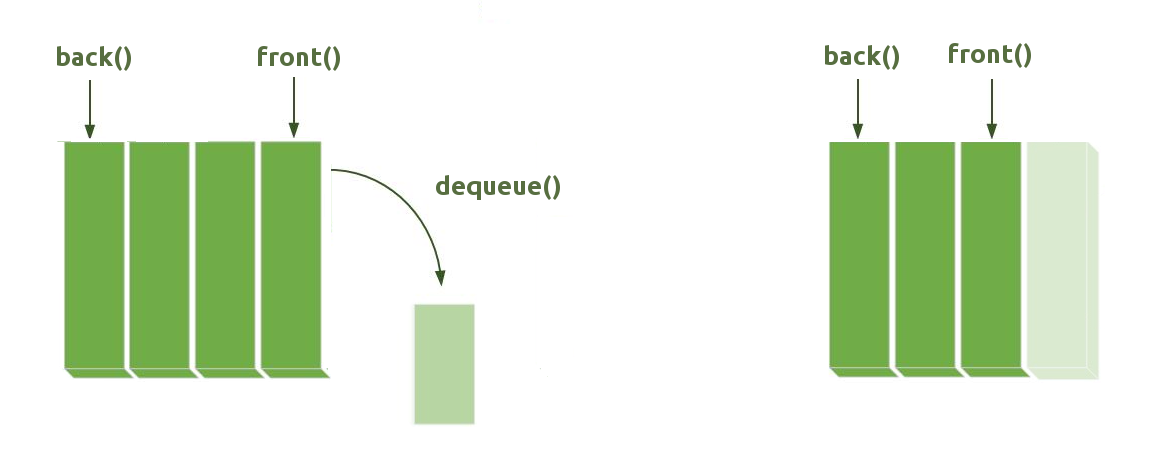
A Queue is a data structure that follows the FIFO (First In First Out) principle. Unlike Stacks, the element inserted first must be the first element to be output.

Conversely, this also means that the last element put into the stack will always end up being the last one that goes out.

We can easily visualize it by imagining a waiting line. Queues are used all throughout programming, here are some examples:

It can perfectly simulate a waiting line.

Used here for a Breadth-First Search (BFS) tree traversal.
Note : A, B, H, C, D, G, I, J, E, F, K, Z.

A Breadth-First Search algorithm generating a minimum spanning tree.

Note: a spanning tree is an acyclic subgraph from a connected and non-directed graph, which connects all the vertices.

A queue acts as a buffer between a task and the service called. It mitigates intermittent overloads (that may result in service failure) by reducing the impact of peak demands (such as a capacitor in electronics).

Operate a queue.
Build our own queue structures.
Put into practice arrays and linked lists.
Understand the advantages / disadvantages of each implementation.

What is next?

If we have not seen the stacks yet, this is the opportunity: they are implemented according to the LIFO principle (Last-In-First-Out) inversely to the queues. We may also continue with more advanced data structures such as: binary trees or hash tables.

We use C++ for code illustration, but no worries, other languages use the same logic and most often a similar syntax.

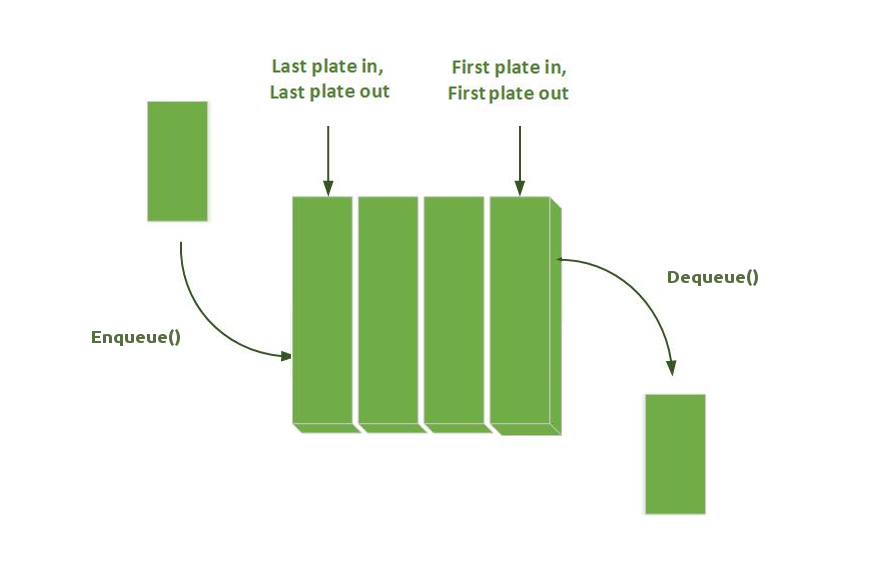
A queue is used for the following two main operations:

  void enqueue(const T& data);  // Add new element at the end of the queue
  void dequeue();               // Remove element from the beginning of the queue

The following features are added to properly use a queue:

  bool empty() const;        // Check if queue is empty
  const T& seek() const;     // Get the data at the front of the queue
 

Example

  queue< string > clients; // Init queue
  clients.enqueue("john"); // ["john"]
  clients.enqueue("do");   // ["john", "do"]
  clients.seek();          // --> "john"
  clients.dequeue();       // ["do"]
  clients.push("jack");    // ["do", "jack"]
  clients.push("dany");    // ["do", "jack", "dany"]

  // Get clients from the first to be handled
  while (!clients.empty()) {
    auto currentClient = clients.seek();
    clients.dequeue();
  }
 

How to build one? Good news! The answer is: pretty easy. We will look at implementations based upon arrays and linked lists in order to decide which best suits our case.

Note: the Queue is an abstract data structure (as the Stack). The definition of their structure is solely based on their behavior and not the underlying implementation. This is in contrast to more fundamental data structures, such as arrays and linked lists, which have strict requirements for how the storage of their data is implemented.

Linked List implementation

We use a linked list with an extra pointer on the back of the queue. Let's take back the skeleton of our structure seen in the 'linked list'.

  template < typename T >
  class Queue
  {
  public:
    Queue() : head(nullptr), tail(nullptr) {}  // Construct as an empty queue
    ~Queue() { ... }                           // Destructor (same as linked list)

  private:
    // Node structure declaration
    struct Node
    {
        // Constructor
        Node(const T& data) : data(data), next(nullptr) {}
        T data;     // Value
        Node* next; // Pointer to the next node
    };

    Node* head; // Pointer on the first element (also the beginning of the queue)
    Node* tail; // Pointer on the last element (also the end of the queue)
  }

When we want to add something to the queue (Enqueue), we just need to add it to the end of the list.

We memorize the last element of the list in order to make effective insertions.

  void Enqueue(const T& data)
  {
    Node* newNode = new Node(data); // Allocate memory

    if (!head)      // First element is the head as well as the tail
    {
      head = newNode;   // Set head to the new node
      tail = head;      // Tail is also the head in this case
    }
    else            // Otherwise element is added at the end
    {
      tail->next = newNode;
      tail = tail->next;  // Update the new tail
    }
  }
  

For the Dequeue operation, nothing is easier: just delete the first item in the list (as in stacks).

  void Dequeue()
  {
    if (!head)  // Empty queue error
      return;

    auto tmp = head;      // Get the current top
    head = head->next;    // Set the head to point to the next node
    delete tmp;           // Delete the node
  }
  

The Empty and Seek functions are also trivial.

  bool Empty() const { return (head) ? false : true; }

  const T& Top() const
  {
    if (!head); // Throw Exception
    return *head;
  }

  

The above implementation gives you the ideas involved, and any optimization may be accomplished by modifying the linked list code.

Array implementation

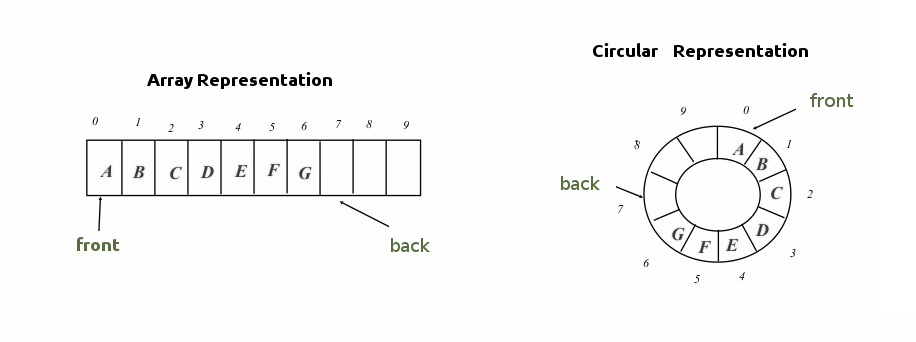
Using a table implementation for a queue is not the simplest approach, but remains very interesting. This involves the use of a circular table often named circular buffer. This is also often used to create caches memory.

  template < typename T >
  class Queue
  {
  public:
    // Allocate/Deallocate stack memory
    Queue(const int size) : back(0), front(0), count(0), max_size(size)
    {  stack = new T[max_size]; }
    ~Queue() { delete[] stack; }

  private:
    int back;           // back index of the queue
    int front;          // front index of the queue
    int count;          // Keep the count to check if full
    const int max_size; // max size
    T* Queue;           // pointer on the array

    Queue(); // Forbid default constructor
  }

When we want to add something to the queue (Enqueue), we just need to add it to the end of the queue and increment counts.

  void Enqueue(const T new_data) {
    if (count == max_size) // Stack overflow exception

    queue[back++] = new_data; // Set data and then update back index
    if (back == max_size)     // Circular iteration if end reached
      back = 0;
    ++count;                  // Update count
  }
  

Dequeue :

  void Dequeue()
  {
    if (count == 0) // Empty queue error
      return;

    if (++front == max_size)     // Circular iteration if end reached
      front = 0;
    --count;  // Change the count
  }
  

Empty and Seek

  bool Empty() const { return count == 0; }
  const T& Seek() const { return queue[front]; }
  

In short

Linked List
Insert and delete operations in O(1).
Can grow dynamically.
Memory allocation/deallocation required for Insert and Delete operations.
Slightly more memory usage due to additional storage of pointers.

Circular Array
Insert and delete operations in O(1).
Can not grow dynamically: it requires a maximum size at initialization.
An oversized table causes amount of wasted memory.
Uses the notion of a circular array (eg. buffers, caches, ...).

• The Algorithm Design Manual Book par Steven S Skiena
• Wikipedia