75x50 Maze generated by a Depth First Search algorithm from Top-Left corner.

Flooding starting from root (Top-Left corner)

The tree representing its data structure topology from root (Top-Left corner).

75x50 Maze generated by a Depth First Search algorithm from Middle.

Flooding starting from root (Middle)

The tree representing its data structure topology from root (Middle).

Depth First Search (DFS) Maze Generator is a randomized version of the depth-first search traversal algorithm. Implemented with a stack, this approach is one of the simplest ways to generate a maze.

Let us first have a look at the DFS traversal algorithm: One starts at any cell and explores as far as possible along each branch before backtracking.

To generate a maze, we have to randomize the traversal: meaning we pick a random but unvisited neighbor to continue our traversal. When we hit a dead end (cell with no unvisited neighbors), we 'backtrack' to the most recent cell in the stack.

Steps

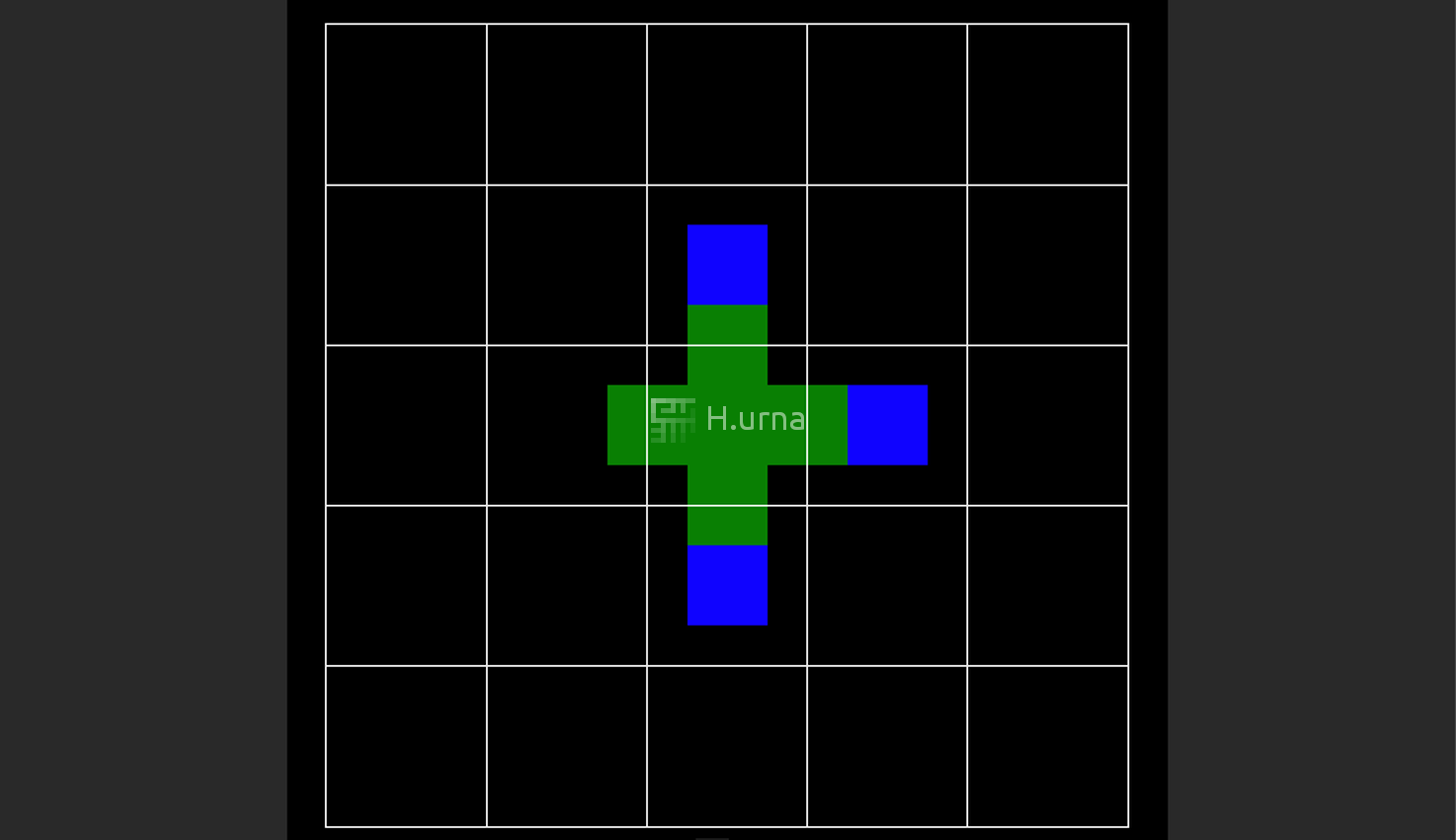
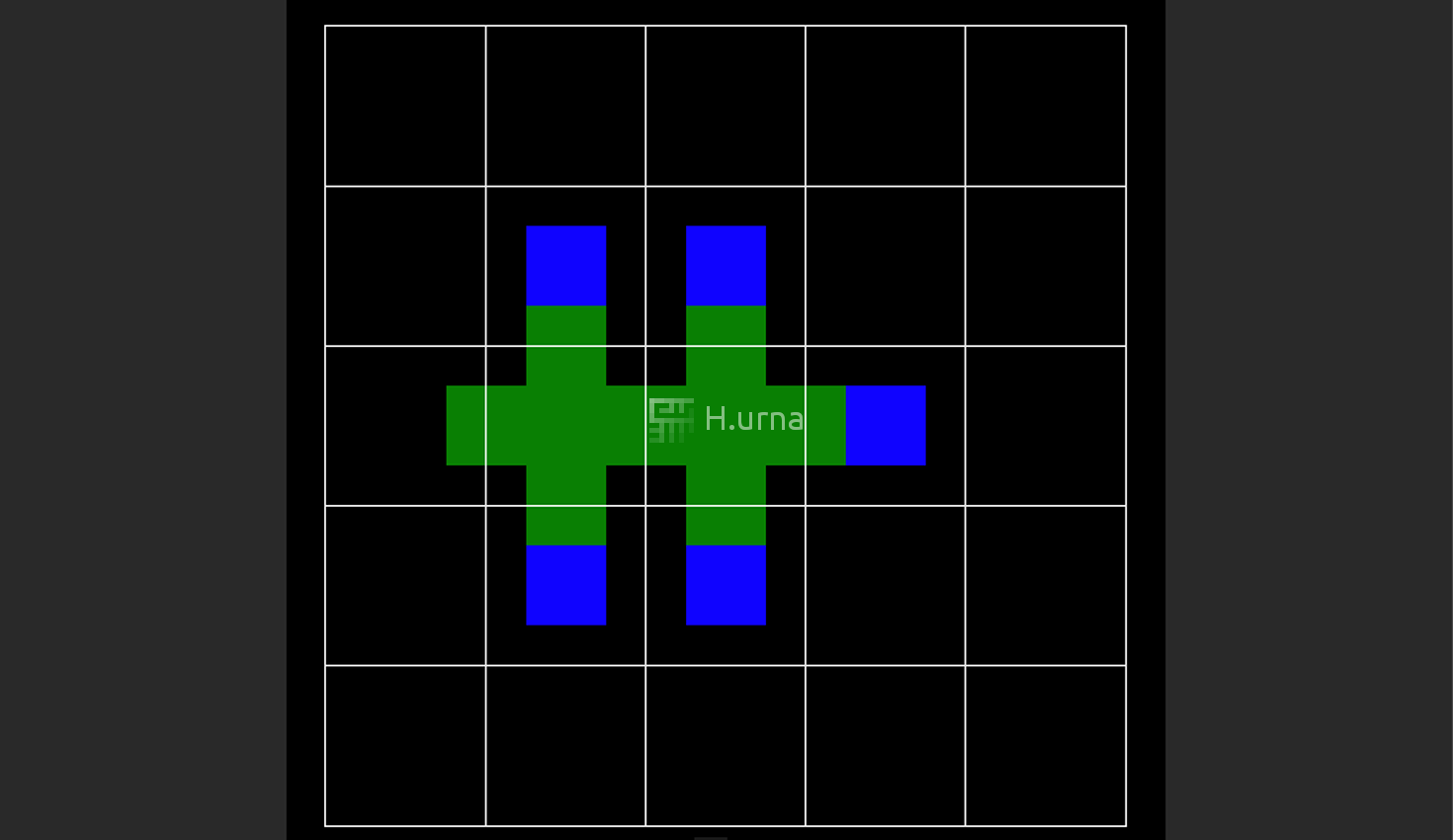
• Choose a starting cell in the field and add it to the stack.
• While there is a cell to be handled in the stack:
• 1. Pop cell from the top of the stack.
• 2. Connect and visit all available neighbors from the bottom, left, right, top and unvisited.
• 3. Randomly select the one to be on the top and Push those neighbors on the stack.

Code

Maze DFS(int width, int height, Cell startCell)
{
  Maze maze(width, height);
  Stack pathStack(startCell);

  // While there is node to be handled in the stack
  while (!pathStack.empty())
  {
    // Handle the cell at the top of the stack:
    // Get available neighbors from bottom, left, right, top and unvisited
    Cell cell = pathStack.pop();
    auto neighbors = GetAvailableneighbors(maze, cell);

    // If there is available node to process (loop to backtrack - 'pop' otherwise)
    if (!neighbors.empty())
    {
      // Randomly select a node to be processed
      auto randIdx = Random() % neighbors.size();

      // For each available node: connect to the cell, mark it as visited
      // and push it into the stack.
      for (auto i = 0; i < neighbors.size(); ++i)
      {
        cell->Connect(Cell::Visite(neighbors[i]));

        // Only the chosen item should be add to the top following a DFS strategy
        if (i != randIdx) pathStack.push(neighbors[i]);
      }

      // Add the chosen node as the next one to be processed
      pathStack.push(neighbors[randIdx]);
    }
  }

  return maze;
} 

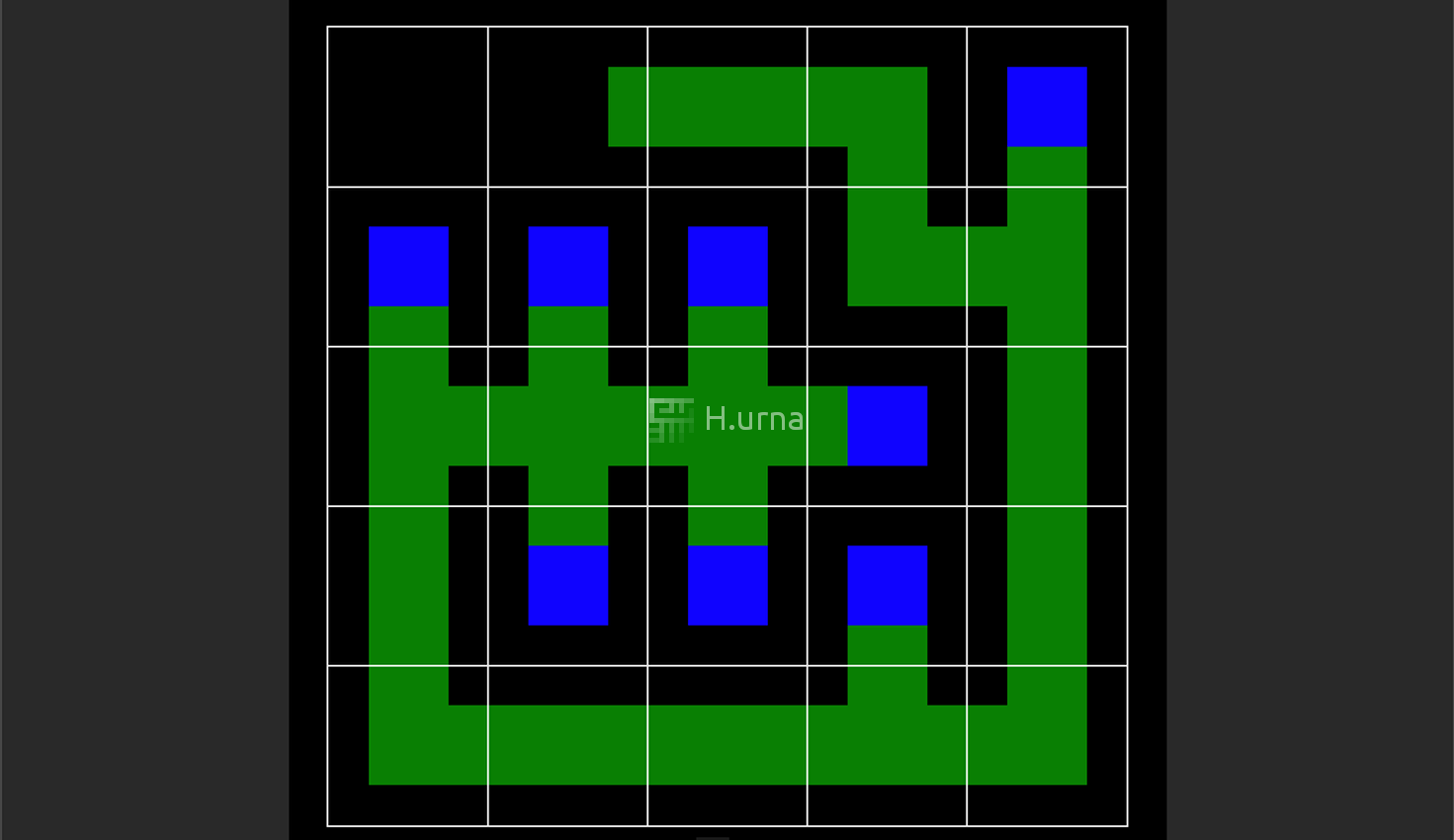
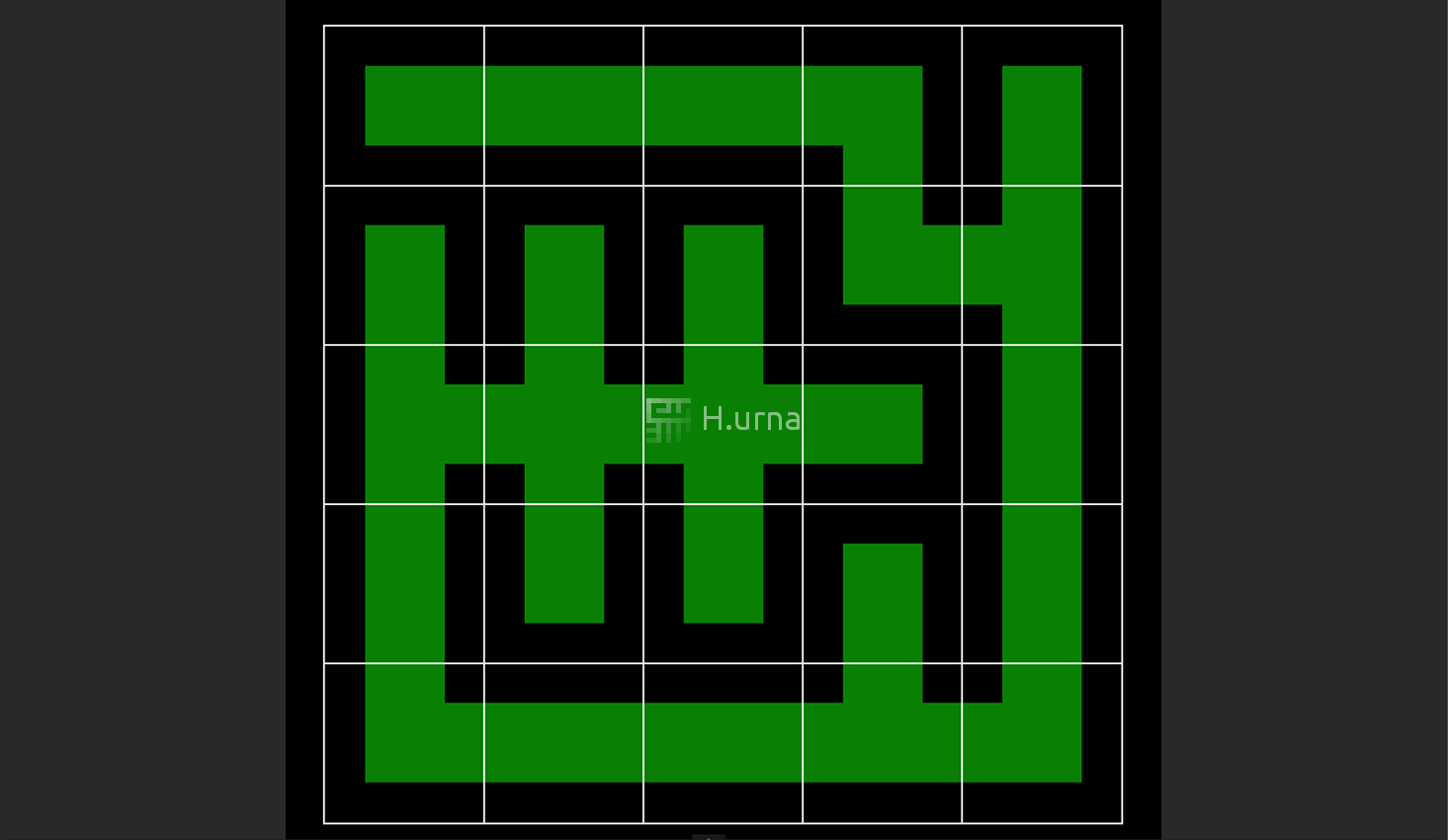
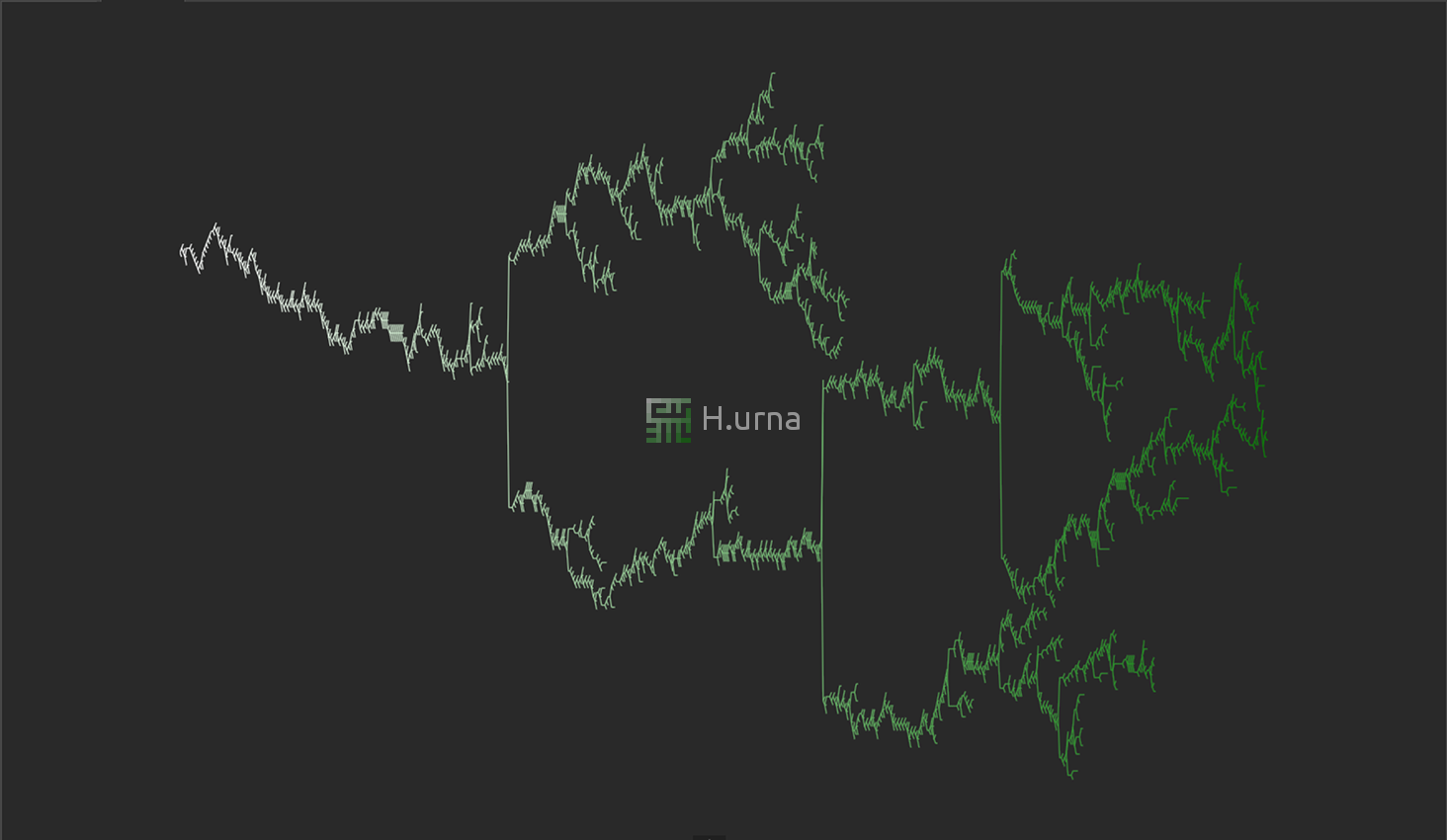
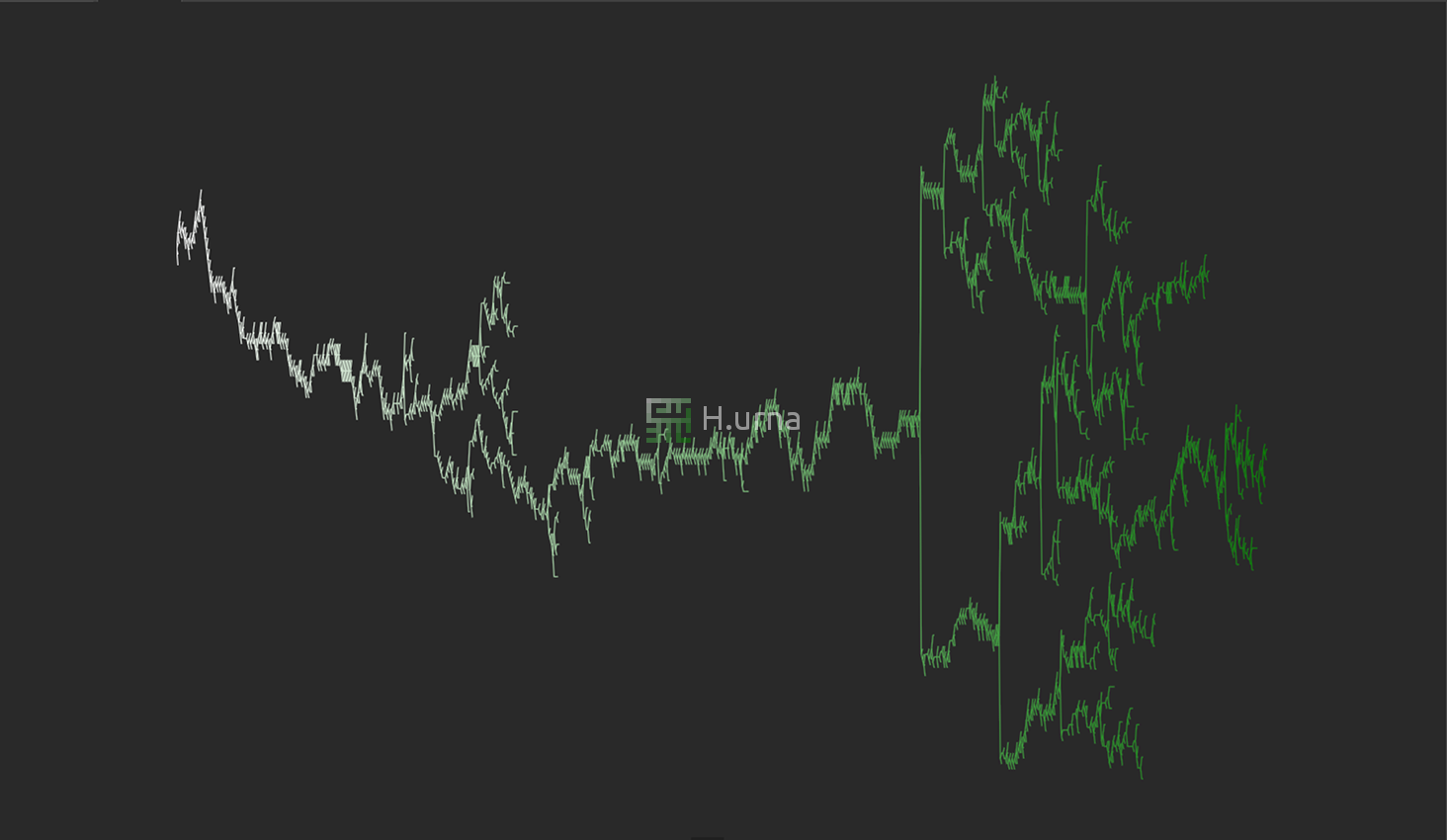
Mazes generated have a low branching factor and contain many long corridors, because the algorithm explores as far as possible along each branch before 'backtracking' (using the previous cell on the stack).

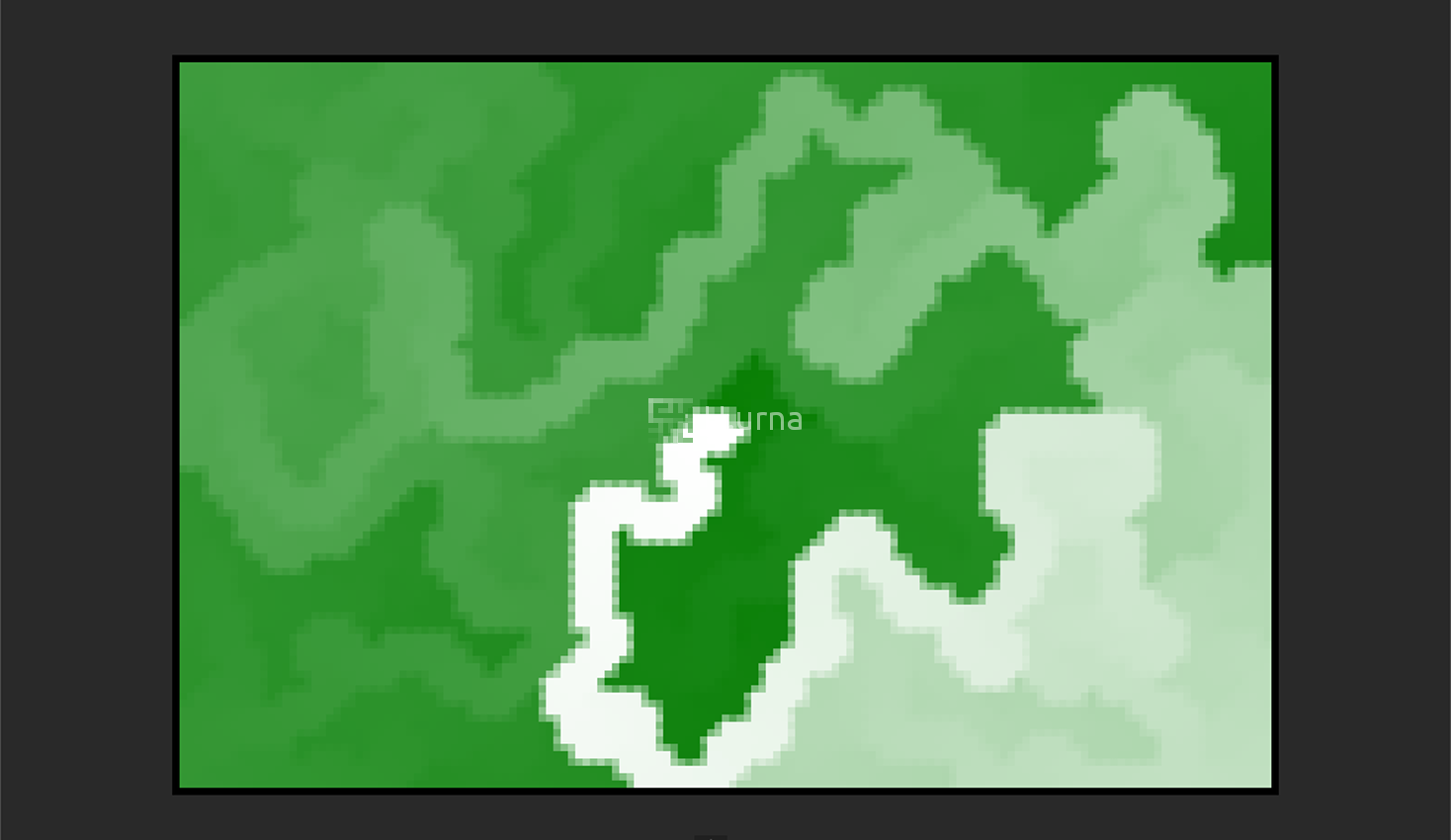
The River characteristic means that when creating the Maze, the algorithm will look for and clear out nearby cells: It flows into the Maze like water. DFS Mazes tend to have a main River, resulting in a large amount of short dead ends.

All of this makes depth-first an excellent algorithm for generating mazes in video games.

In mazes generated by that algorithm, it will typically be relatively easy to find the way to the root since most paths lead to or from there, but it is hard to find the way out.

1. DFS can be started anywhere; let's start it on the middle.

2. Connect and visit all available neighbors from: bottom, left, right, top and unvisited. The West cell (randomly selected) will be added at the end and its path extended (cf. next slide).

Blue colored cells mean being within the stack and waiting to be processed.

3. West cell is added and then processed. Once again the West cell got selected to extend the path.

4. After few iterations, the algorithm got close of having visited all cells.

5. All cells are processed, stack cell is empty: Maze is done!