Accès Rapide
Description
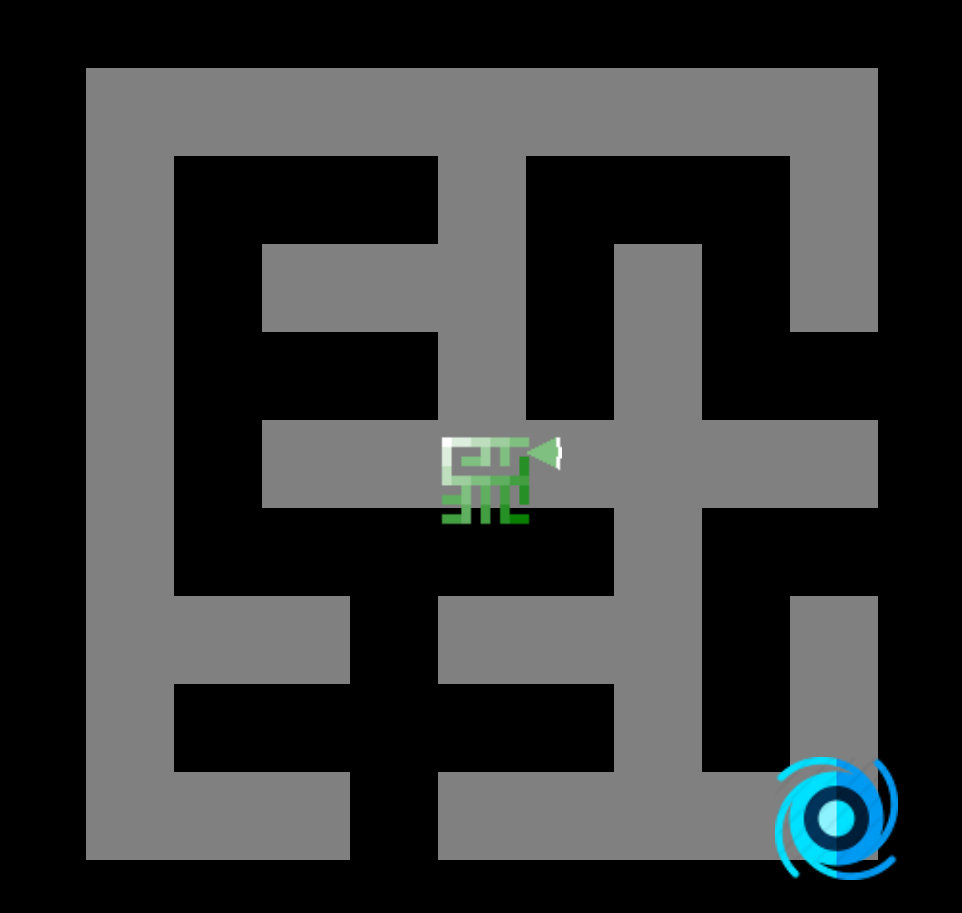
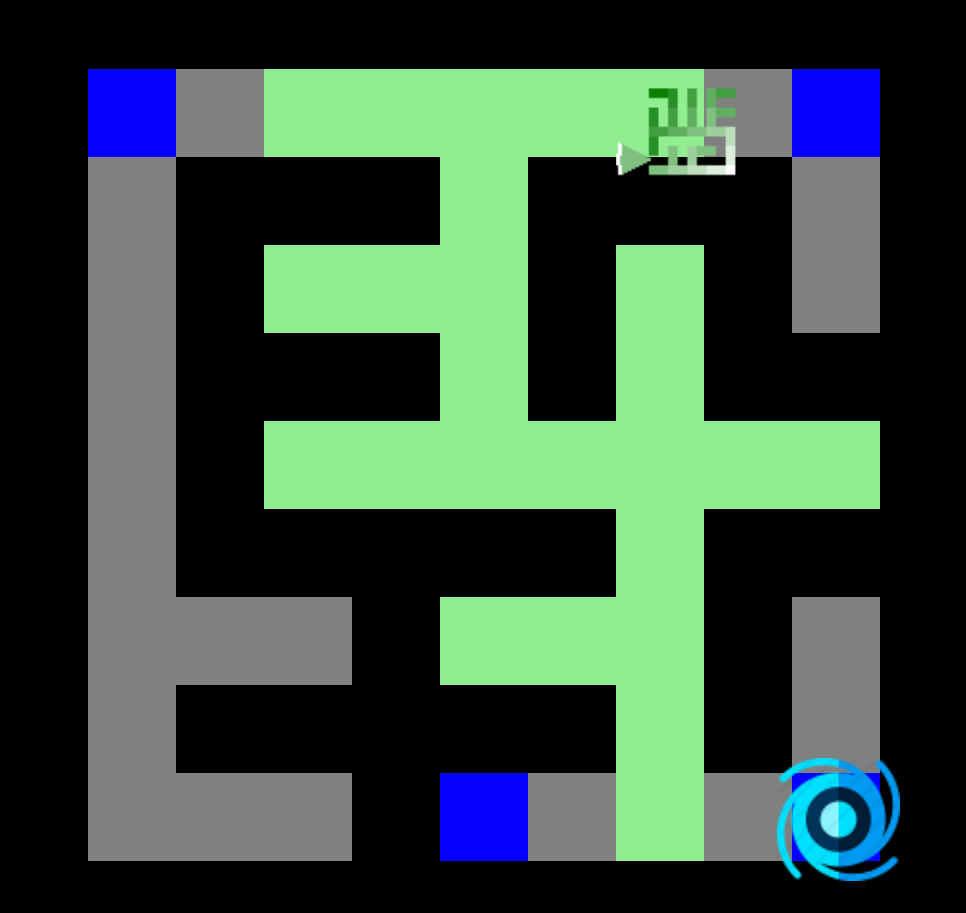
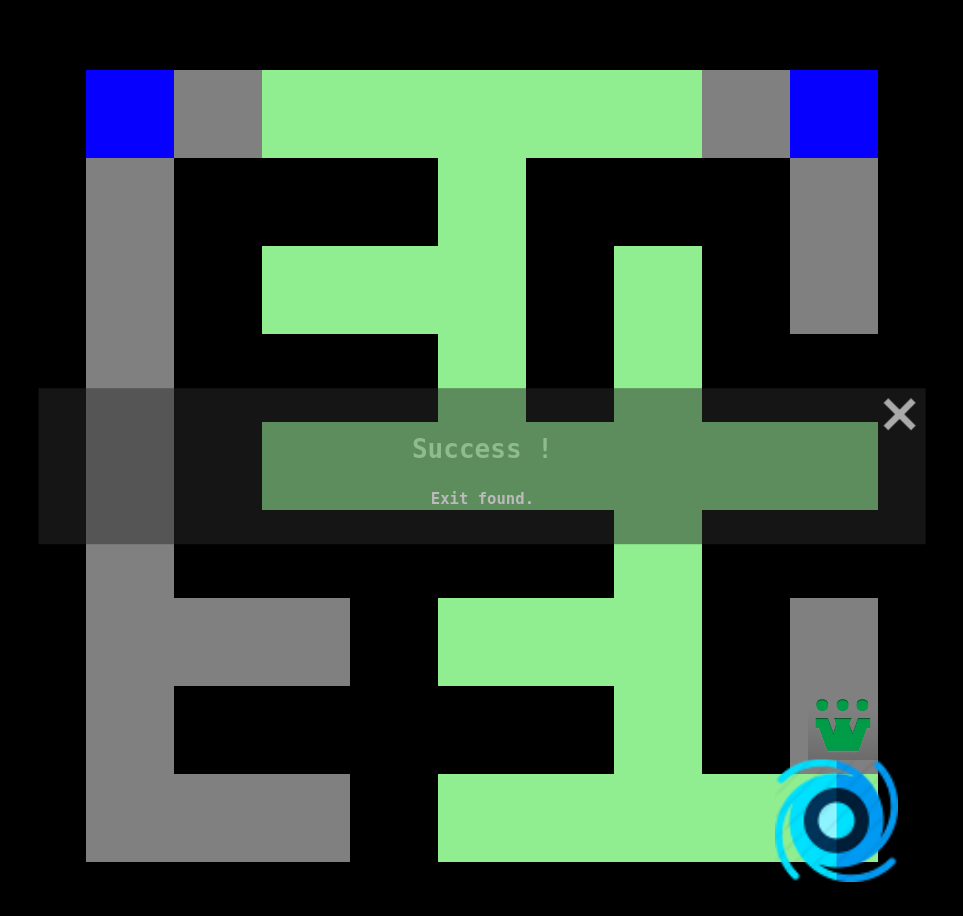
La recherche en largeur, ou BFS (Breadth Firt Search), est l’un des deux algorithmes fondamentaux concernant le parcours de graphes. Construit en 1959 par Edward F. Moore pour trouver le chemin le plus court dans un labyrinthe, cet algorithme est utilisé quotidiennement. Non seulement pour les parcours de graphes, mais aussi pour l'analyse de réseaux, dans nos GPS, pour les moteurs de recherche, pour la planification et d'autres types d’analyses.
En bref: c'est un algorithme incroyablement utile qui garantit le chemin le plus court entre deux nœuds (lorsque les connexions ont le même coût).
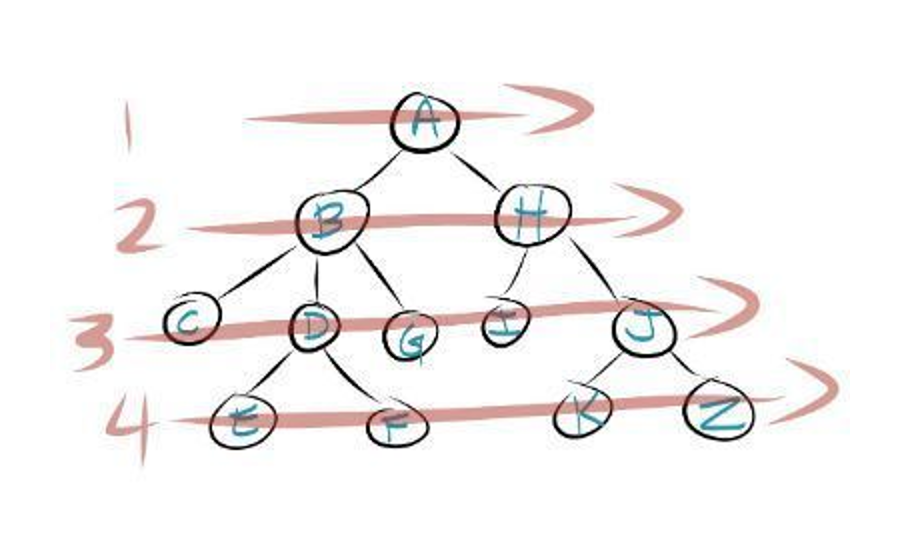
BFS explore également dans toutes les directions jusqu'à ce que l'objectif soit atteint. En d'autres termes, il commence à partir d'un nœud et examine tous ses voisins dans un premier temps, puis il examine tous les voisins des voisins, et ainsi de suite ... Si nous considérons un arbre (qui est un graphe simplifié), le BFS procédera comme suit:
Construction
Étapes
- Ajouter le nœud de départ dans la file d'attente (queue) et le marquer comme visité.
- Tant qu'il y a un noeud en attente dans la file:
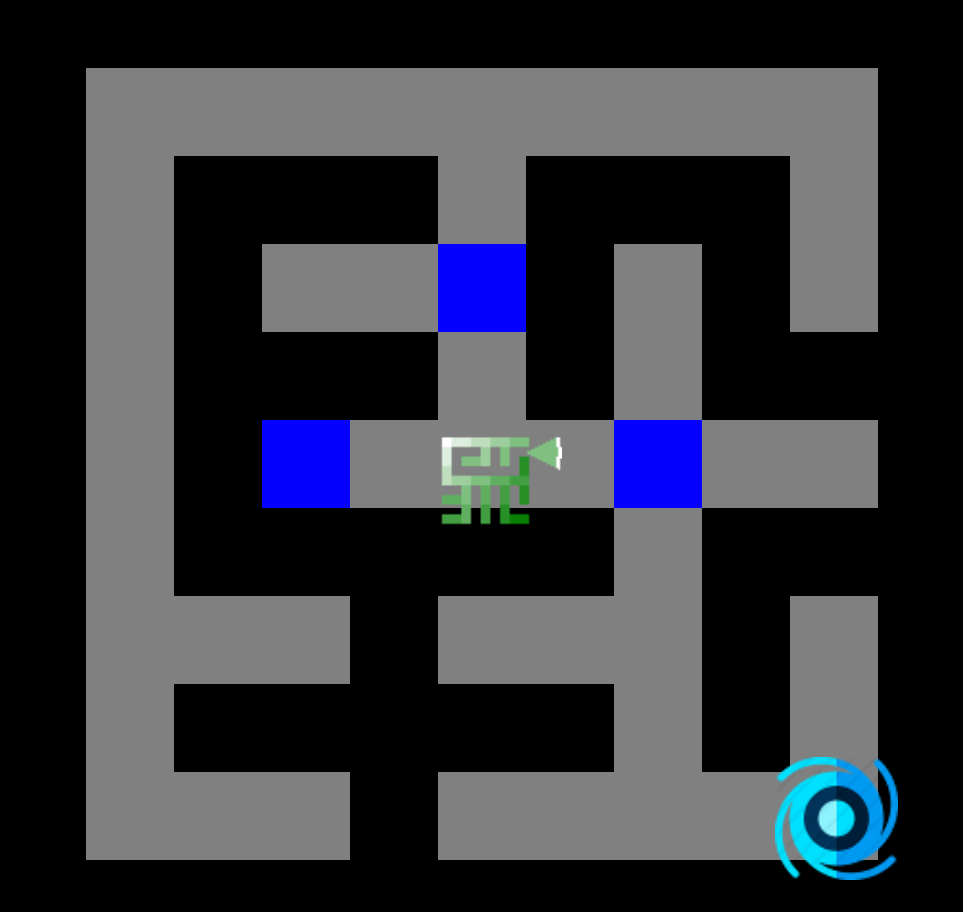
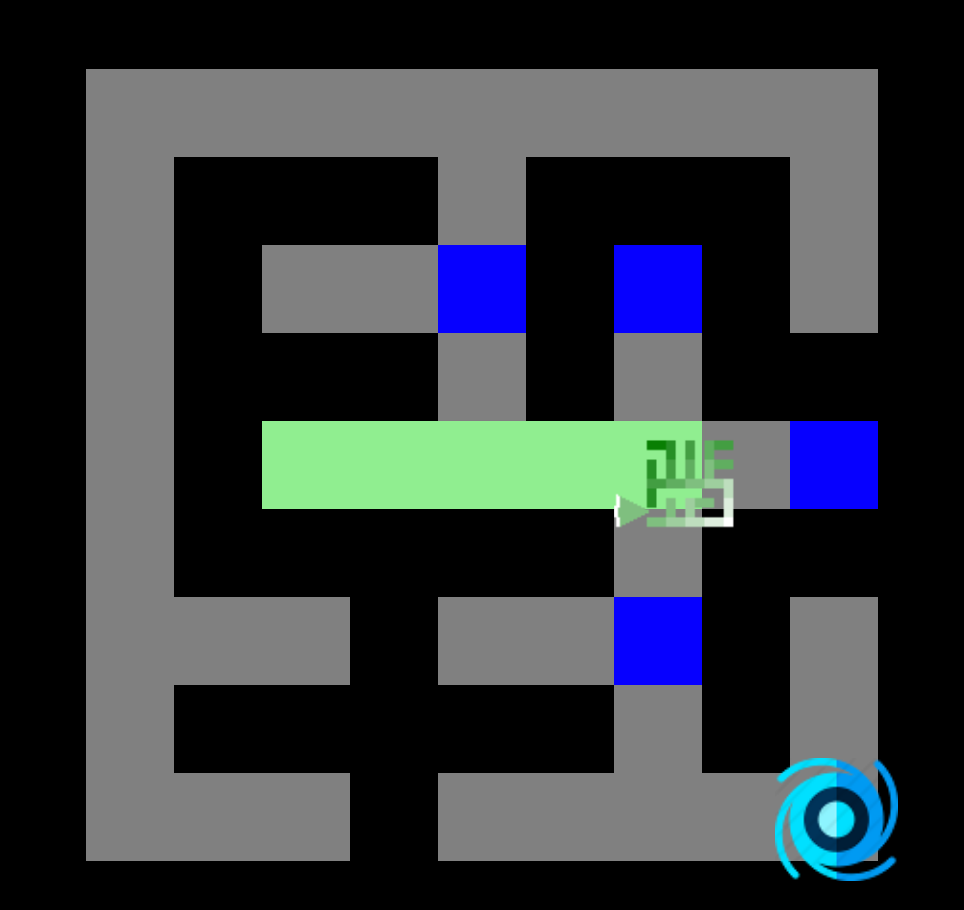
- 1. Prendre le nœud à l'avant de la file d'attente.
- 2. Ajouter ses voisins non visités dans la file, noter le parent et marquer comme visité
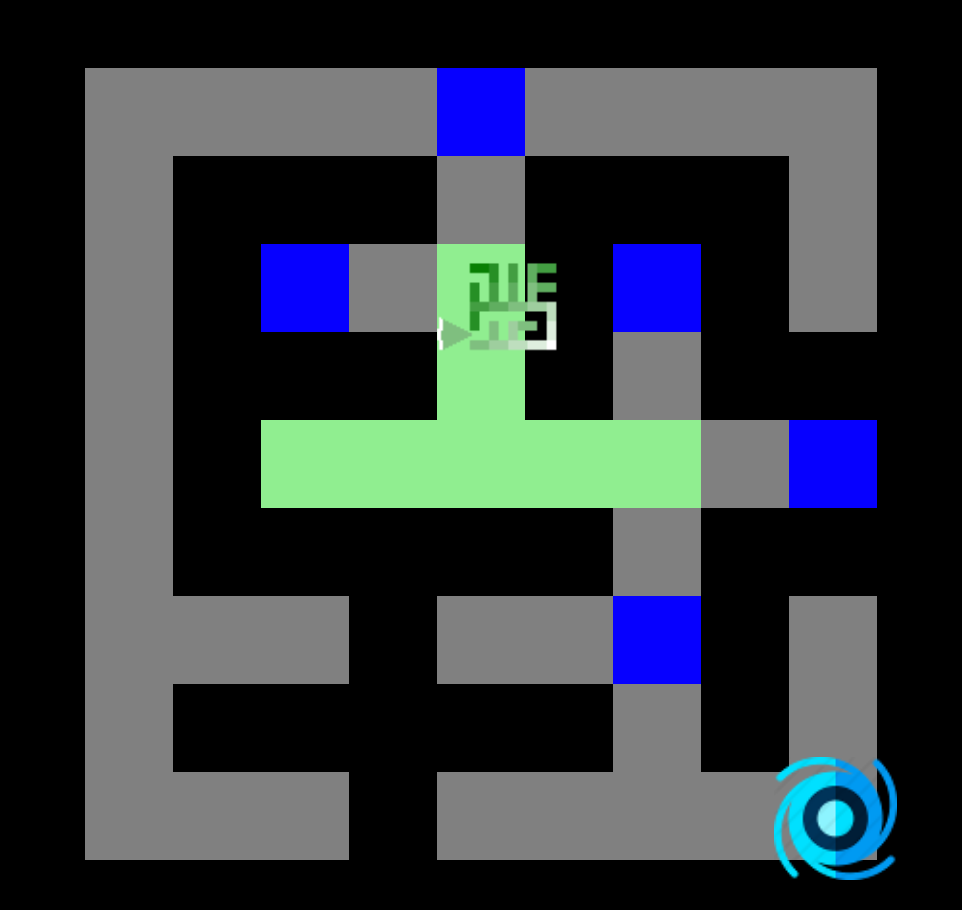
- Fini : remonter le chemin avec le lien parent afin d'obtenir le chemin le plus court.
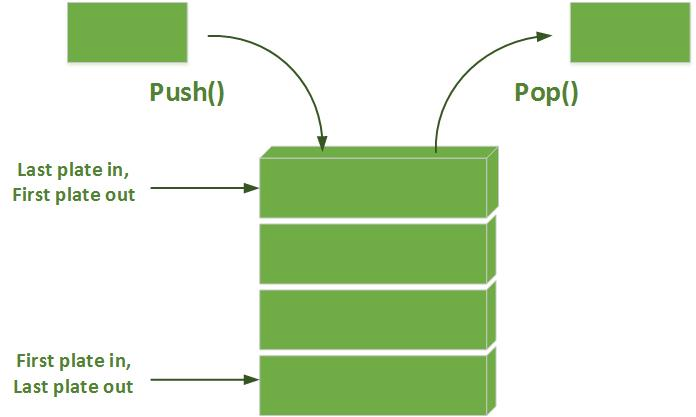
BFS utilise la stratégie opposée à celle de la recherche en profondeur (DFS). qui explore plutôt un chemin aussi loin que possible avant d’être forcé de revenir en arrière. Pourtant, les deux algorithmes ont les mêmes lignes de code; la seule différence réside dans la structure de données utilisée:
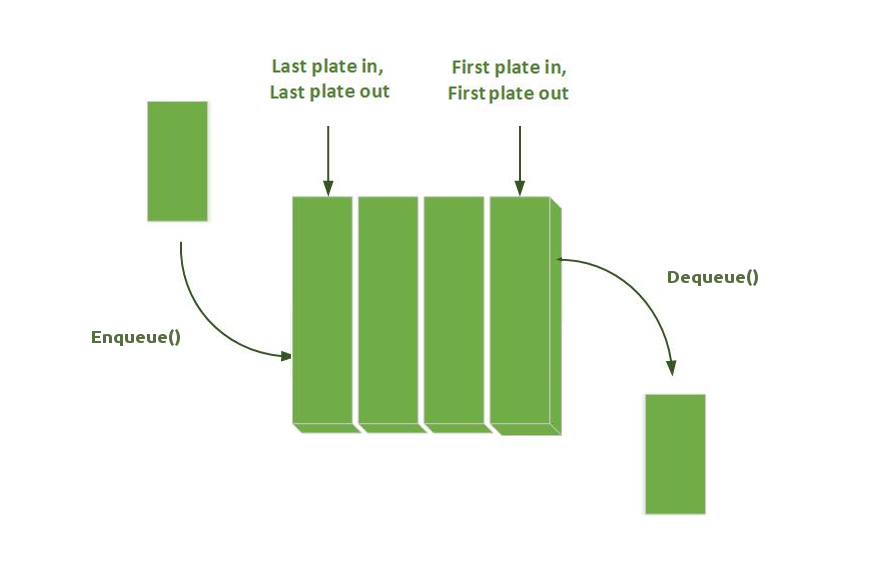
|
|
| BFS utilise une Queue (FIFO) | DFS utilise une Pile, ou Stack, (LIFO) |
|---|
Cet algorithme est, par rapport au DFS, un peu plus délicat à implémenter de manière récursive. Nous verrons donc uniquement l'approche itérative ;)
Code
BFS(Maze maze, Node start, Node end)
{
// Put the start node in the queue
start.visite = true;
Queue queue(start);
// While there is node to be handled in the queue
while (!queue.empty())
{
// Handle the node in the front of the lineand get unvisited neighbors
Node curNode = queue.pop();
// Terminate if the goal is reached
if (curNode == end)
break;
// Take neighbors, set its parent, mark as visited, and add to the queue
auto neighbors = curNode.GetUnvisitedNeighbors();
for (auto i = 0; i < neighbors.size(); ++i)
{
neighbors[i].visite = true;
neighbors[i].parent = curNode;
queue.push(neighbors[i]);
}
}
// Done ! At this point we just have to walk back from the end using the parent
// If end does not have a parent, it means that it has not been found.
}



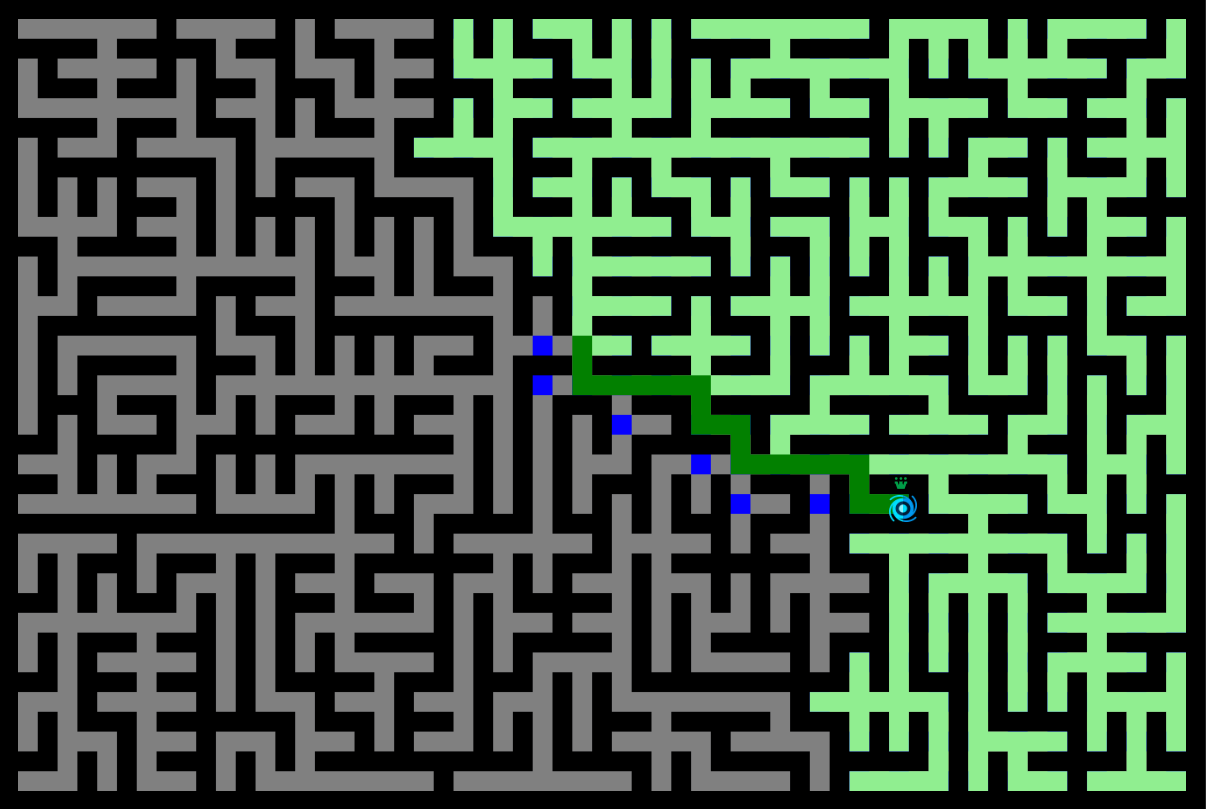
 Jouer en ligne
Jouer en ligne