Accès Rapide
Applications
- Utilisée comme routine dans l'algorithme Tri Fusion (En-Place)
Construction
L'aggrégation En-Place prend en entrée deux listes triées et en sort une seule contenant tous les éléments triées en sortie. Elle peut être utilisée comme routine dans divers algorithmes de tri, le plus connu étant le tri par fusion.
L’idée est de comparer chaque valeur de la première séquence (pointeuri) avec le premier élément de la deuxième séquence (pivot). Si le pivot est plus petit que le pointeuri, on permute les deux éléments et déplacons ensuite le plus grand dans la deuxième séquence afin de le mettre à sa place (les listes restent ordonnées).
Etapes
- 1. Obtenenir 2 pointeurs au début de chaque séquence : pointeuri et pivot.
- 2. Pour chaque valeur de la première séquence, si pointeuri <= pivot :
- Échanger pointeuri et pivot.
- Déplacer le nouveau pivot à sa bonne position dans la deuxième séquence en le faisant glisser successivement avec son plus proche voisin (de droite).
Code
void AggregateInPlace (Iterator begin, Iterator pivot, Iterator end)
{
if (distance(begin, pivot) < 1 || distance(pivot, end) < 1)
return;
// Use second half as receiver
for(auto curBegin = begin; curBegin < pivot; ++curBegin)
{
if (Compare(curBegin, pivot))
continue;
// Place it at the beginning of the second list
swap(curBegin, pivot);
// Displace the higher value in the right place of the second list by swapping
auto it = pivot;
for (; it != end - 1; ++it)
{
if (Compare(it, (it + 1)))
break;
swap(it, (it + 1));
}
}
}
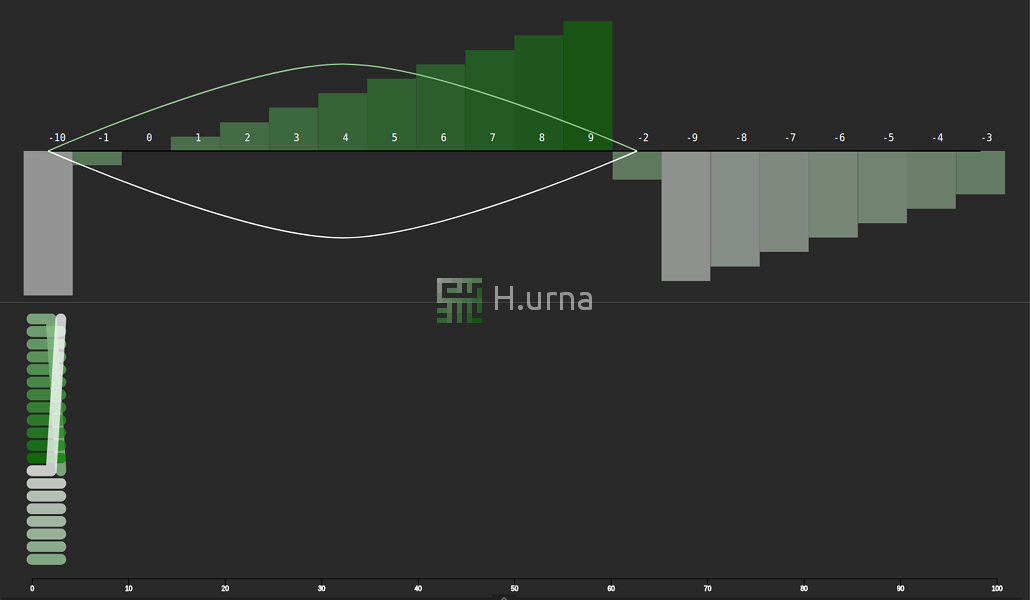
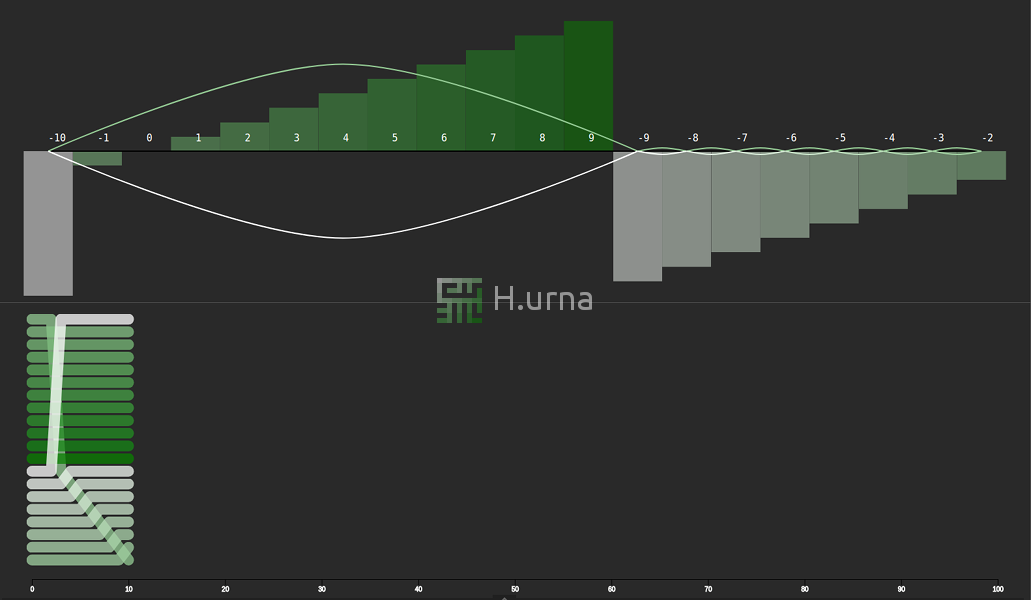
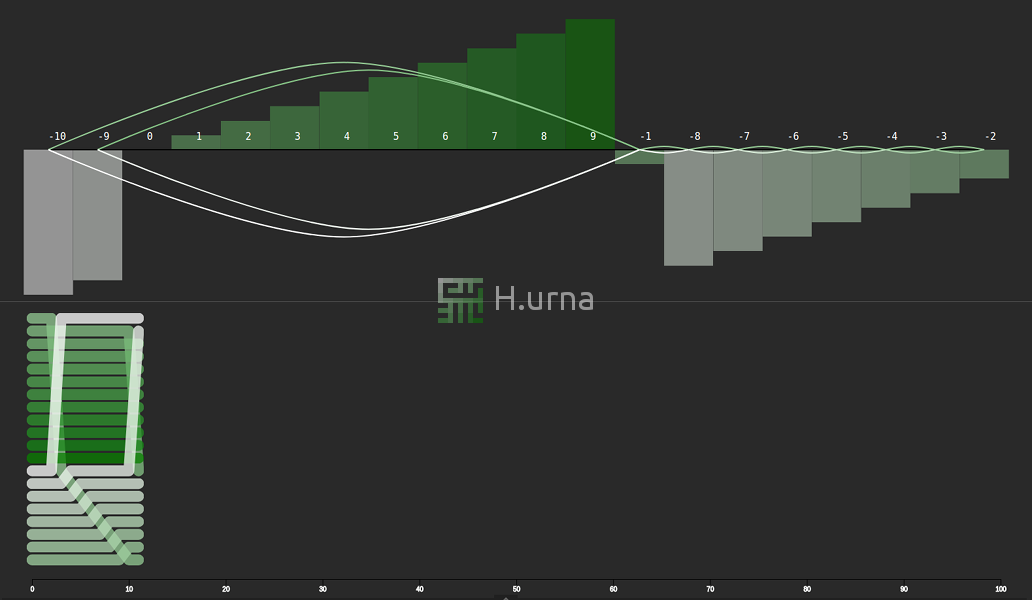
Visualisation
Optimisation
La complexité de traitement peut être optimisée en utilisant simplement la plus petite séquence à parcourir au lieu de toujours la première.
Complexité
Rappel
Théorèmes mathématiques utiles:
$$\sum_{i=0}^{n-1} {C}^{ste} = n * {C}^{ste}$$Temps
Notation:
- n : nombre d'éléments dans la première séquence
- m : nombre d'éléments dans la deuxième séquence
Meilleure
La meilleure configuration se produit lorsque tous les éléments de la deuxième séquence sont plus petits que ceux de la première séquence; cela revient à dire que la séquence est déjà complètement triée.
Par conséquent, nous ne devons parcourir la première séquence qu’une seule fois avec : O(n) pour la version de base. O(min(n, m)) en utilisant la petite séquence (cf. optimisation).
Pire
Le pire cas O(n * m) se produit lorsque tous les éléments de la la première séquence sont plus grands que ceux de la seconde. Cela signifie que min(Séquence1) > max(Séquence2); ainsi, chaque fois que nous itérons:
- 1. Echanger pointeuri et pivot
- 2. Déplacer le nouveau pivot à la fin de la deuxième séquence
Séquences
$$a_0 = m$$ $$a_1 = m$$ $$...$$ $$a_i = m$$
Calcul
$$S(n) = \sum_{i=0}^{n-1} m$$ $$S(n) = n * m$$ $$\Theta(n) = O(n*m)$$
Mémoire
L'agrégation en-place n'utilise pas de stockage ni ne fait de récursivité. Elle requière donc O(1) d'utilisation mémoire dans tous les cas.


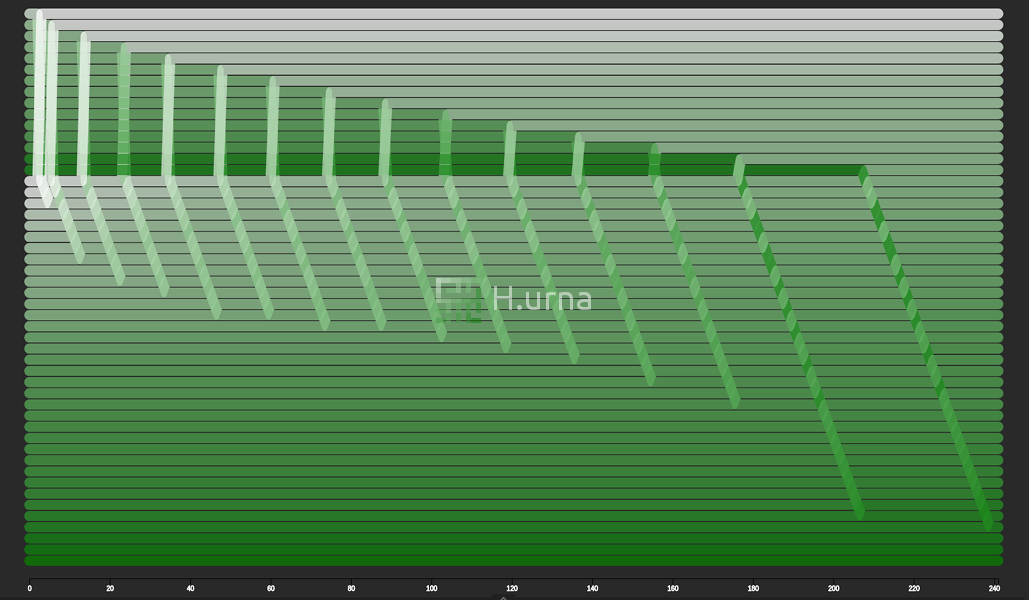
 Jouer en ligne
Jouer en ligne
 Code Source C++
Code Source C++