Traces laissées par un Tri Fusion sur une séquence aléatoire {50}

Lignes d'échanges laissées par un Tri Fusion sur une séquence aléatoire {50}

Traces laissées par un Tri Fusion sur une séquence décrcoissante {50}

Lignes d'échanges laissées par un Tri Fusion sur une séquence décrcoissante {50}

Dépendances

• Utilise l'Agrégation-En-Place en sous-routine

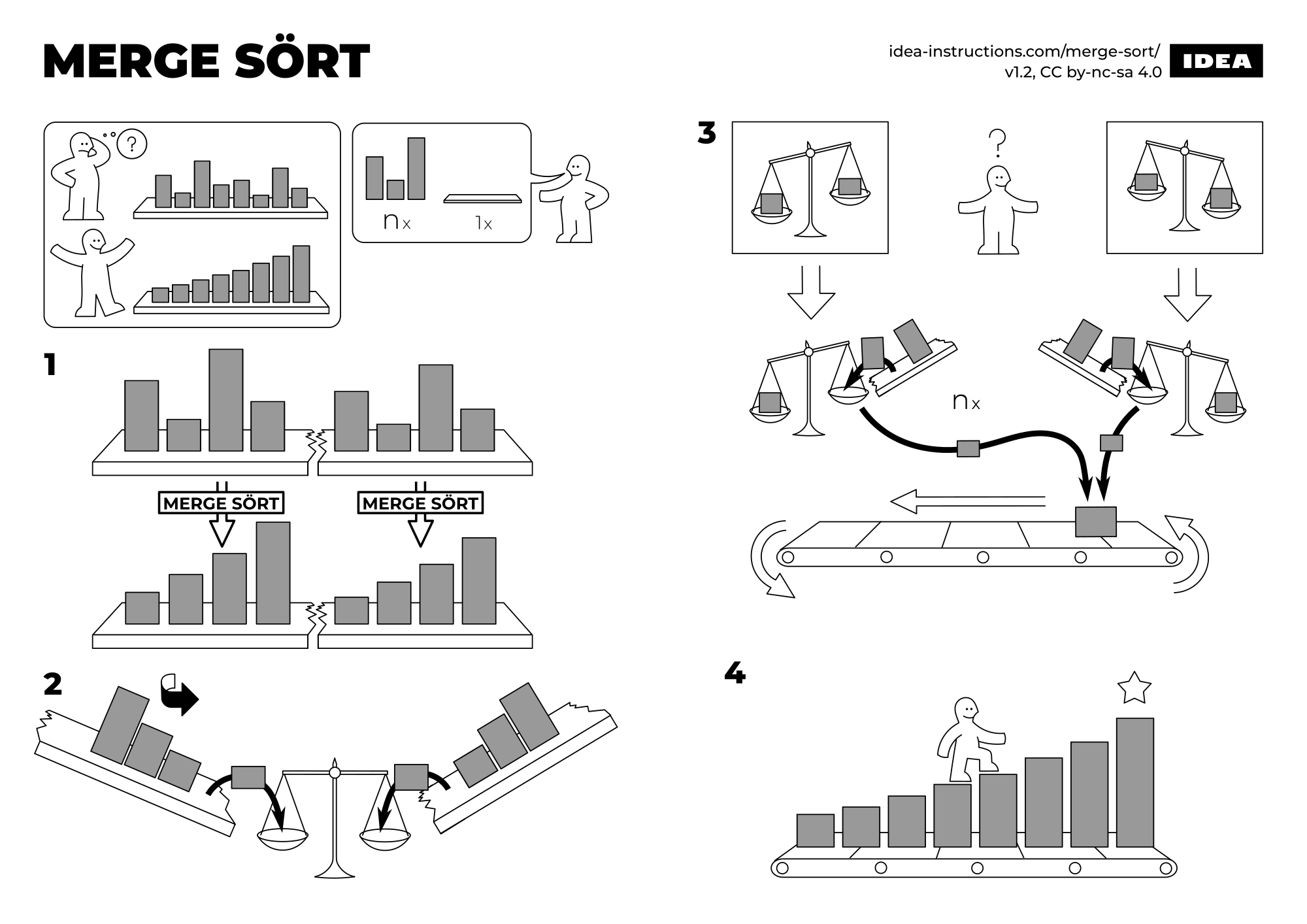
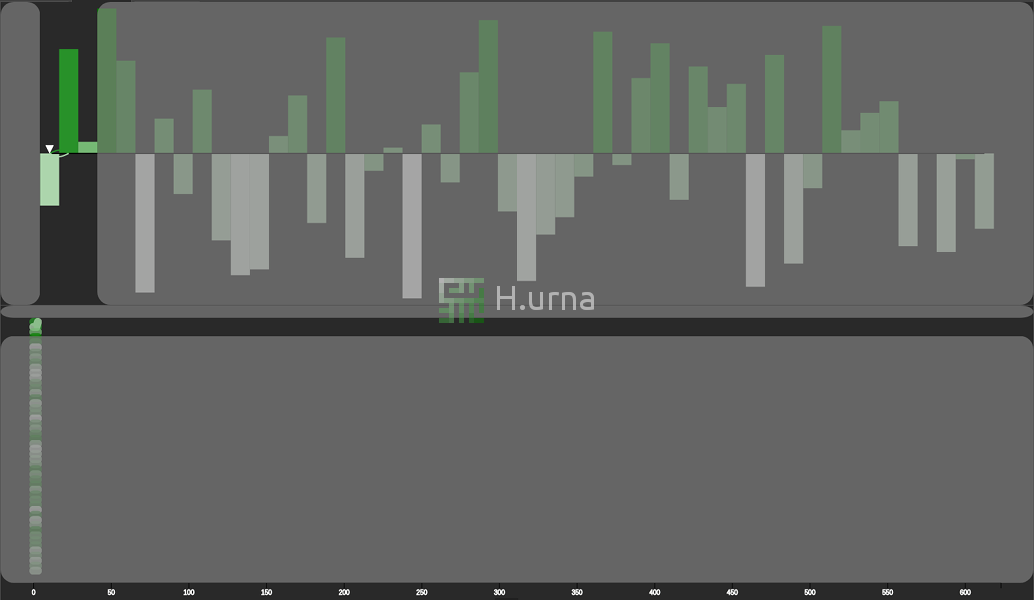
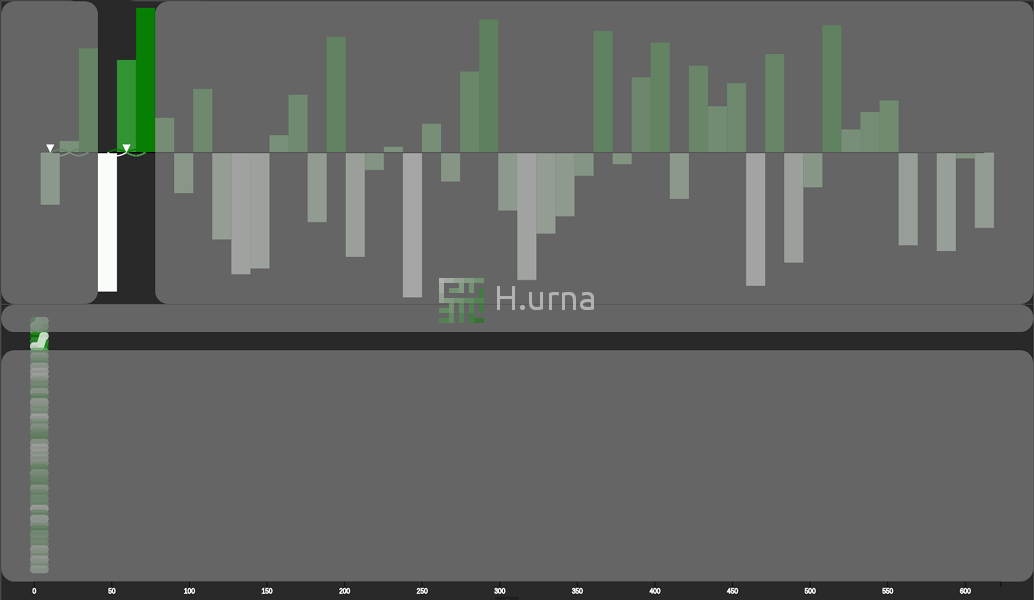
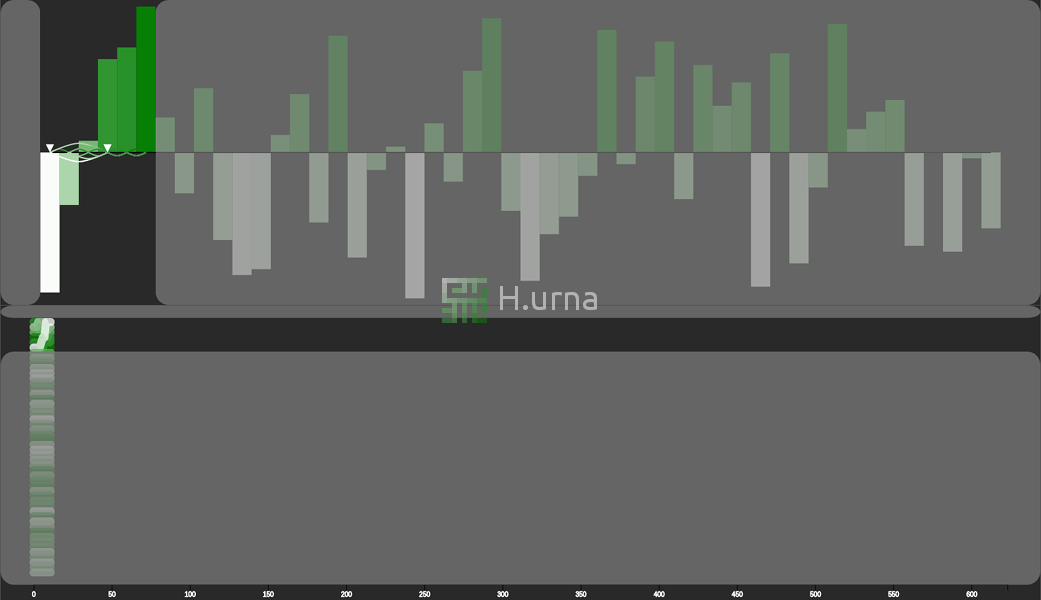
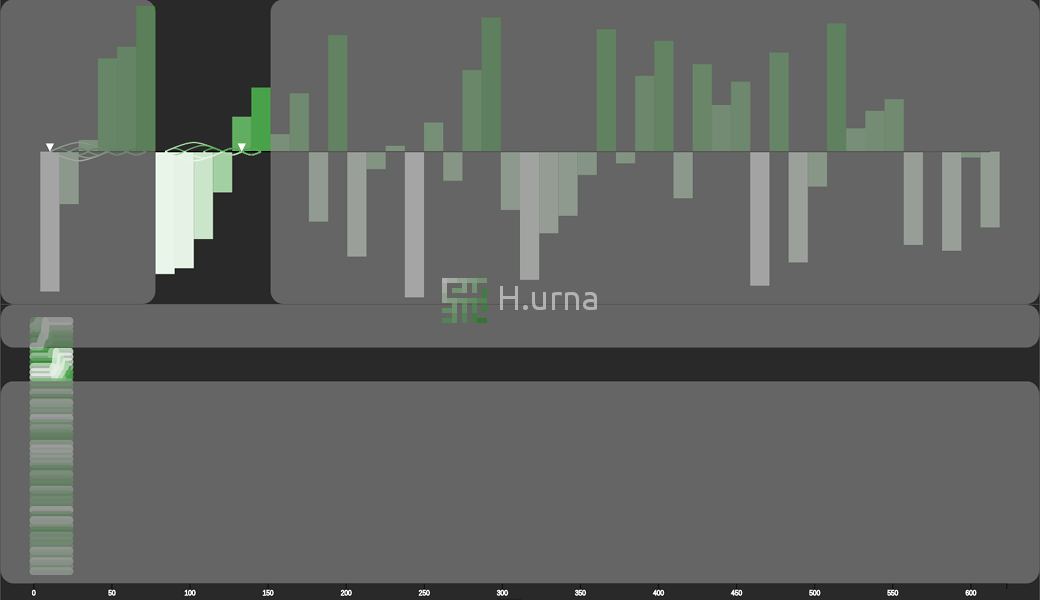
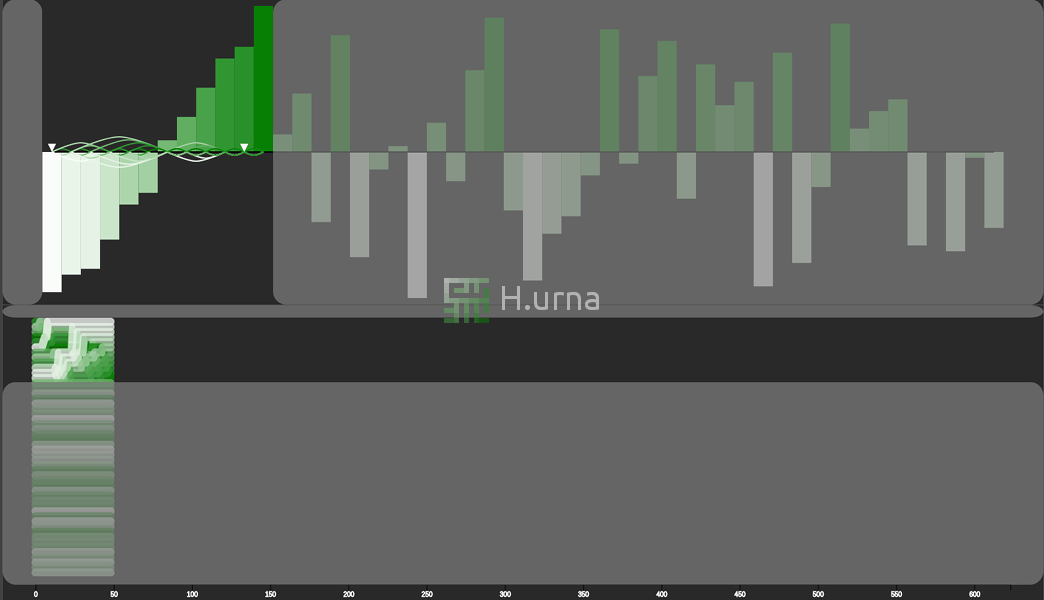
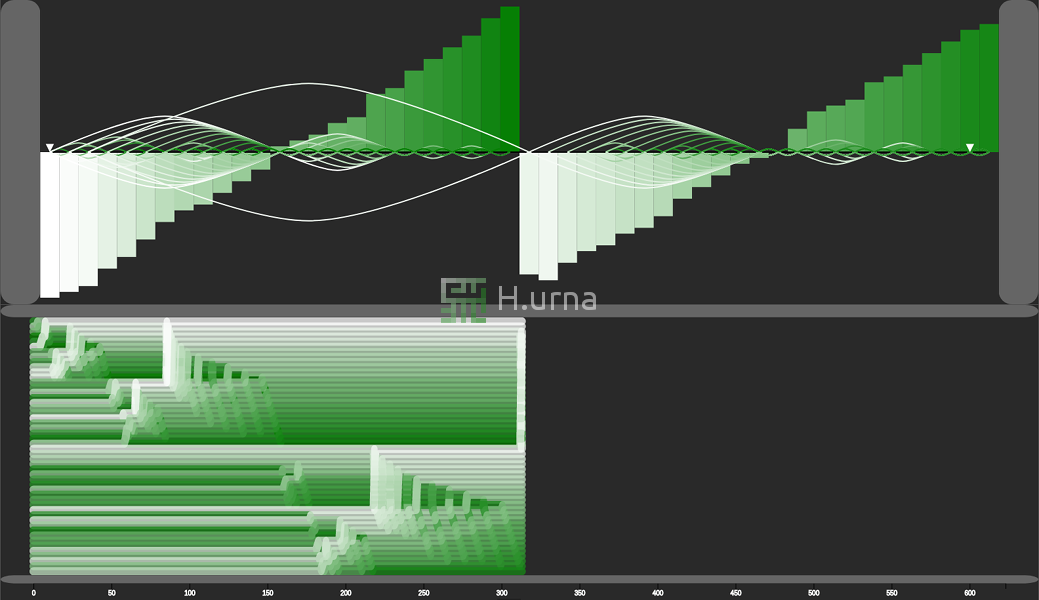
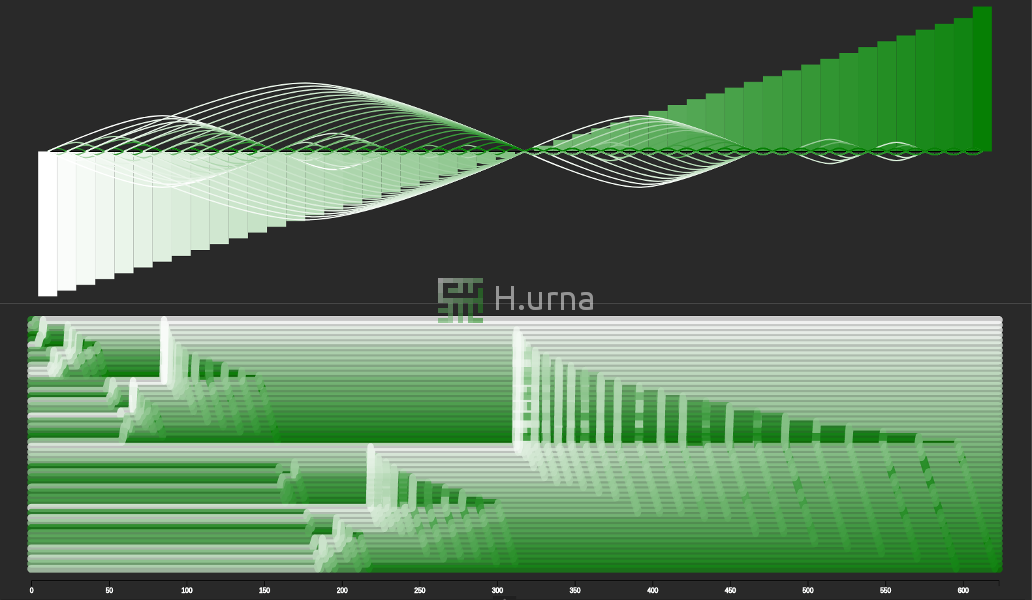
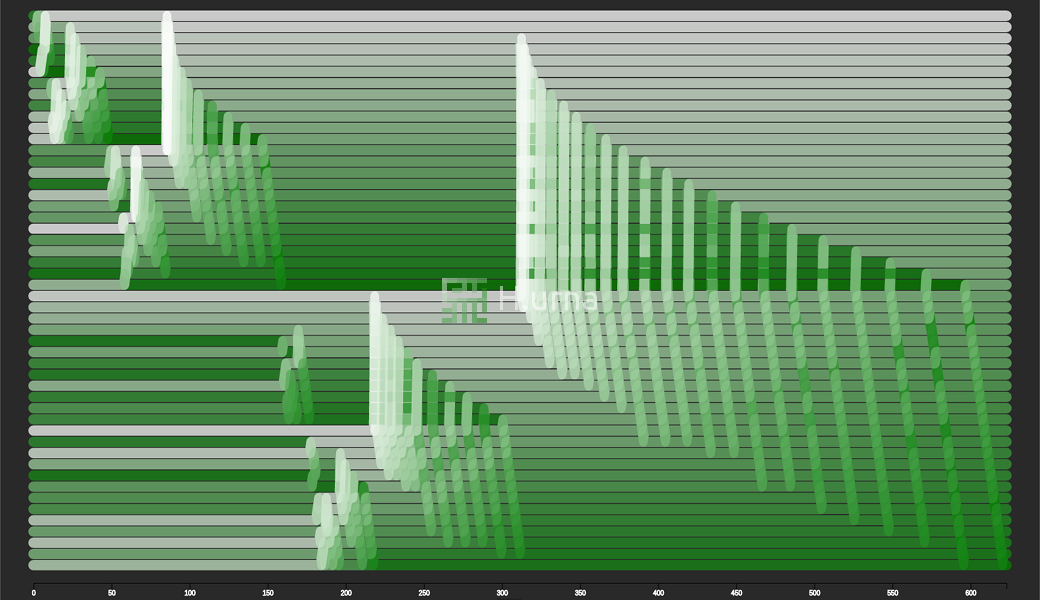
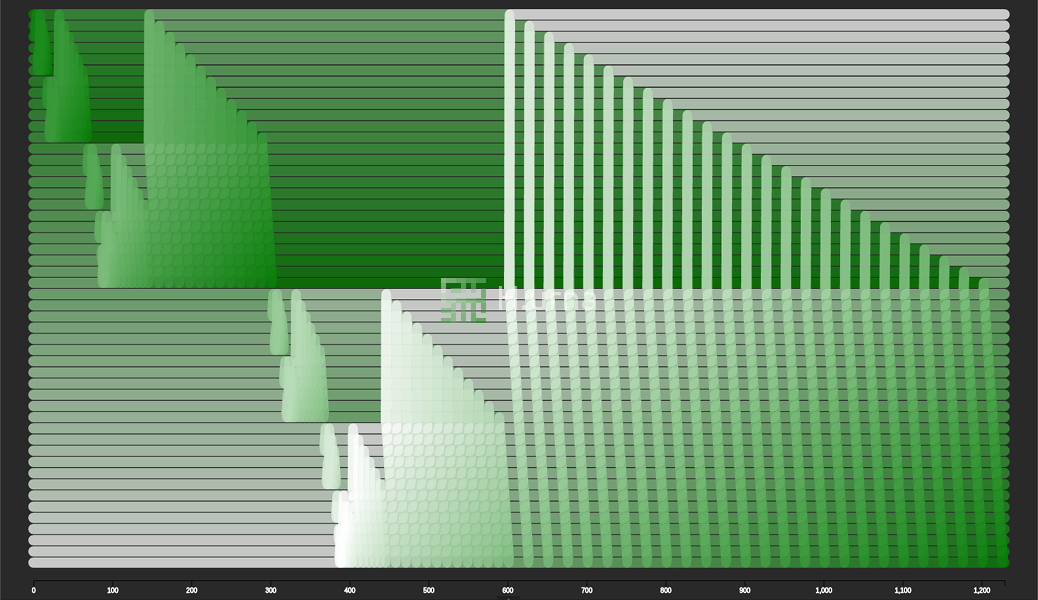
Le tri Fusion (ici En-Place) fonctionne en stratégie ascendante. Initialement, il fusionne deux sous-séquence de taille 1 (elles sont trivialement triées). Chaque séquence (une paire d’éléments résultant de cette première fusion) est ensuite fusionnée / agrégée en une nouvelle séquence triée contenant les deux (4 éléments). Ce processus est répété jusqu'à ce que toutes les séquences soient fusionnées (et donc triées).

Etapes

• 1. Sélectionner le milieu du tableau.
• 2.a. Faire une récursion sur la partie gauche.
• 2.b. Faire une récursion sur la partie droite.
• 3. Fusionner les deux séquences.

Code

void MergeSort(Iterator begin, Iterator end)
{
  const auto size = distance(begin, end);
  if (size < 2)
    return;

  auto pivot = begin + (size / 2);

  // Recursively break the vector into two pieces
  MergeSort(begin, pivot);
  MergeSort(pivot, end);

  // Merge the two pieces
  Merge(begin, pivot, end);
}

En arrivant au bas de la récursion gauche, les sous-séquences (triviales) sont fusionnées.

Toujours dans la récursion principale gauche, c'est maintenant au tour de la sous-récursion de droite de fusionner les sous-séquences (triviales).

La récursivité remonte d'un niveau : les deux séquences ont été fusionnées.

Le même processus dans la partie droite de la récursion.

La fusion se fait avec les deux parties.

Ici, nous sommes remonté au premier niveau de récursion et nous pouvons voir très clairement les deux moitiés de la séquence respectivement triées.
Commence alors la dernière fusion.

La denière fusion est faite : le tri est fini.

Rappel

La version en place de l'agrégation a une complexité temporelle en:

• O(n/2) ~ O(n) dans le meilleur des cas. Ici : m = n/2
• O(n²/2) ~ O(n²) dans le pire des cas. Ici : m = n/2
• Une complexité spatiale en O(1) dans tous les cas.

Théorème principal pour les récurrences de type diviser pour régner (Divide and Conquer Recurrences)

Temps

Meilleure

La meilleure configuration se produit lorsque tous les éléments sont déjà triés ou presque triés.
Cela signifie que chaque Fusion / Agrégation se comportera tel un algorithme en O(n). Mettons cela dans une relation de récurrence directement: $$T(n) = O(n) + T(\frac{n}{2}) + T(\frac{n}{2})$$ $$T(n) = O(n) + 2T(\frac{n}{2})$$ Il suffit d'utiliser ensuite le théorème principal pour les récurrences de type divide-and-conquer: O(n log n).

Moyenne / Pire

Le pire cas O(n²) se produit lorsque tous les éléments de la la première séquence sont plus grands que ceux de la seconde lors de la fusion. (cf. agrégation en place).
Mettons cela dans une relation de récurrence: $$T(n) = O(n) + T(\frac{n^2}{2}) + T(\frac{n^2}{2})$$ $$T(n) = O(n) + 2T(\frac{n^2}{2})$$

Avec le théorème principal pour les récurrences de type divide-and-conquer : O(n²).

Mémoire

Rappel:
- L'aggregation en place nécessite O(1) d'espace mémoire.
- Les récursions sont ici faites les unes après les autres. Ceci est appelé récursion de queue et signifie que celle de droite commence seulement après que celle gauche ai terminé son processus. Cela implique que la récursion de droite ne s'ajoute pas à la pile d'appels (de fonctions) de celle de gauche.

Dans ce cas, la notion "en place" peut être assouplie pour signifier "utilisation de l'espace de pile d'appels logarithmique", qui est la quantité d'espace requise par l'utilisation de la pile d'appels des fonctions.

Parallélisation

S’agissant d’un algorithme ascendant de type divide and conquer, le travail peut être facilement scindé et les traitements effectués par différentes unité de calcul (ou threads). Cela le rend extrêmement utile pour les systèmes hautes performances traitant de grandes quantités de données.

L'algorithme parallélisé reste aussi simple : il suffit d'effectuer chaque récursion de tri dans des threads séparés, puis les joindre au moment de la fusion / agrégation.

void MergeSort(Iterator begin, Iterator end)
{
  const auto size = distance(begin, end);
  if (size < 2)
    return;

  // Fork both sequence
  auto pivot = (begin + end) / 2;
  thread thread1 = MergeSort(begin, pivot);
  thread thread2 = MergeSort(pivot, end);

  // Join them
  thread1.join();
  thread2.join();

  // Merge the two pieces
  Merge(begin, pivot, end);
}