Quick Access
Dependencies
- Use Aggregate-In-Place algorithm as a subroutine
How To Build
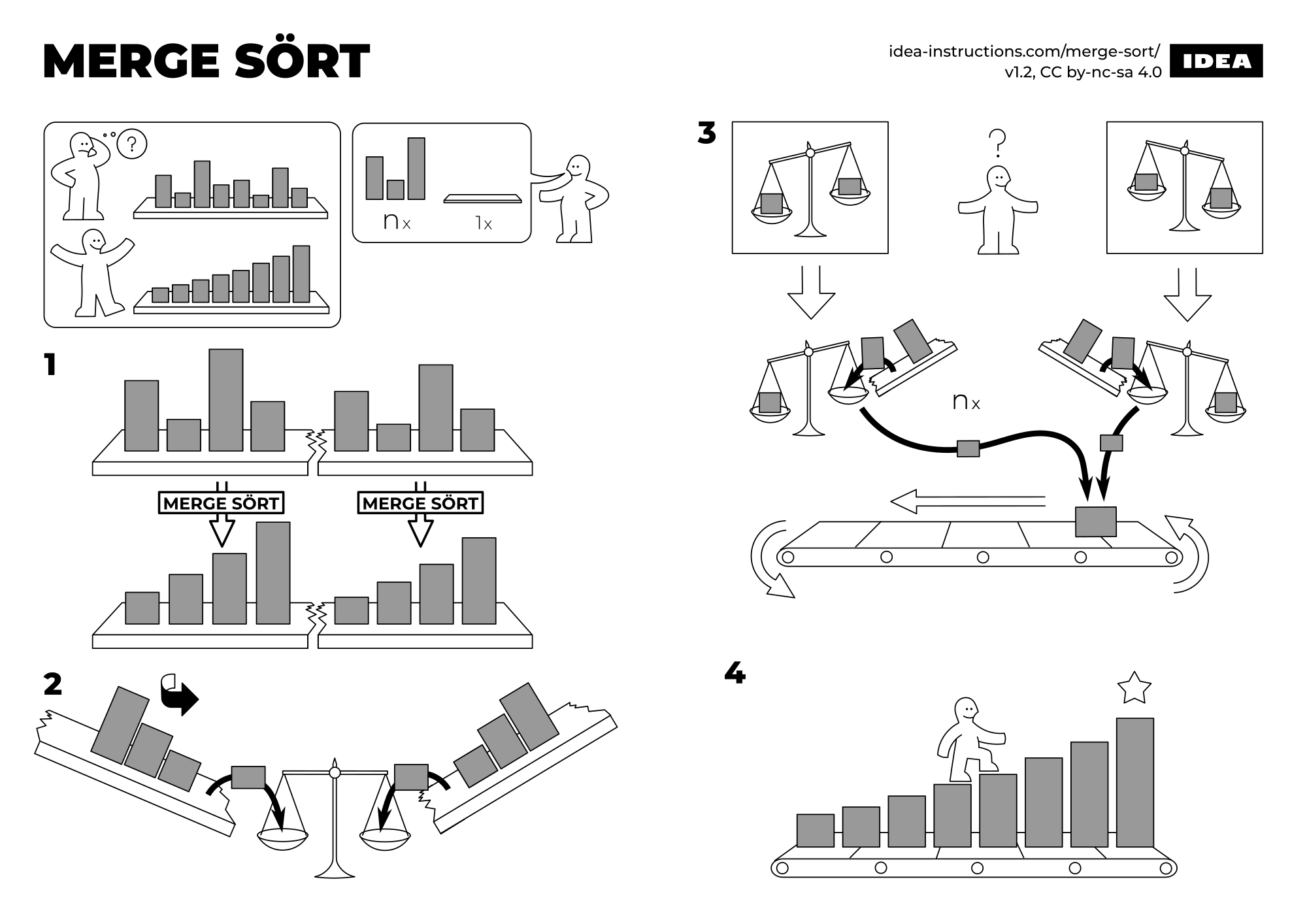
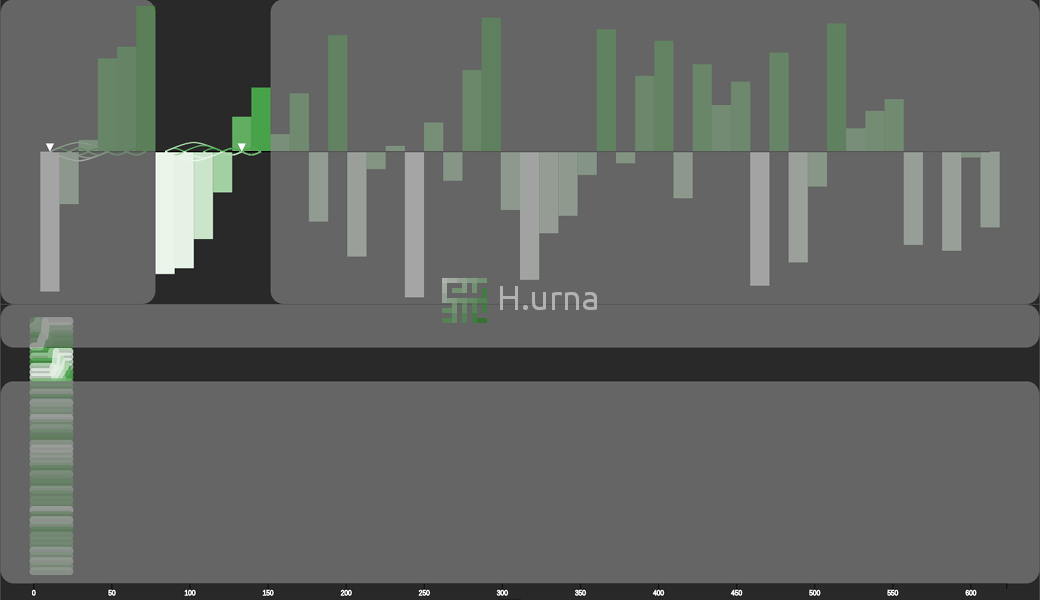
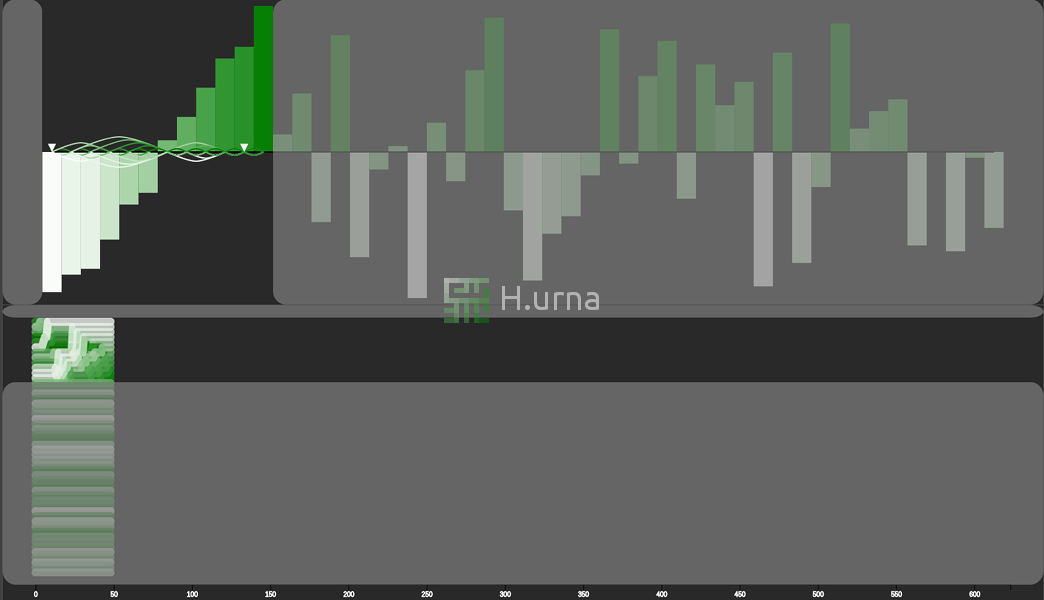
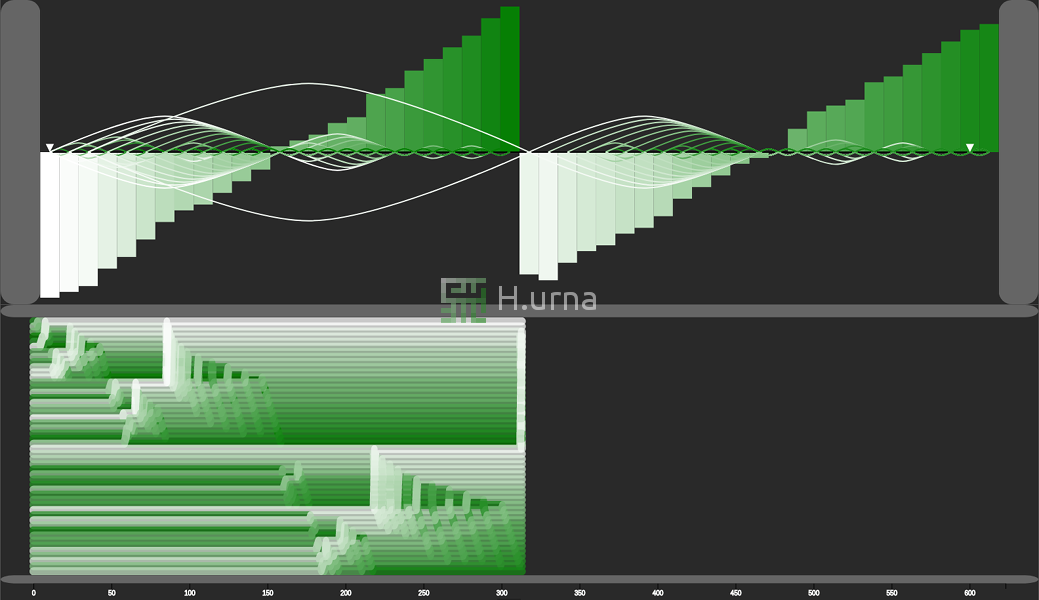
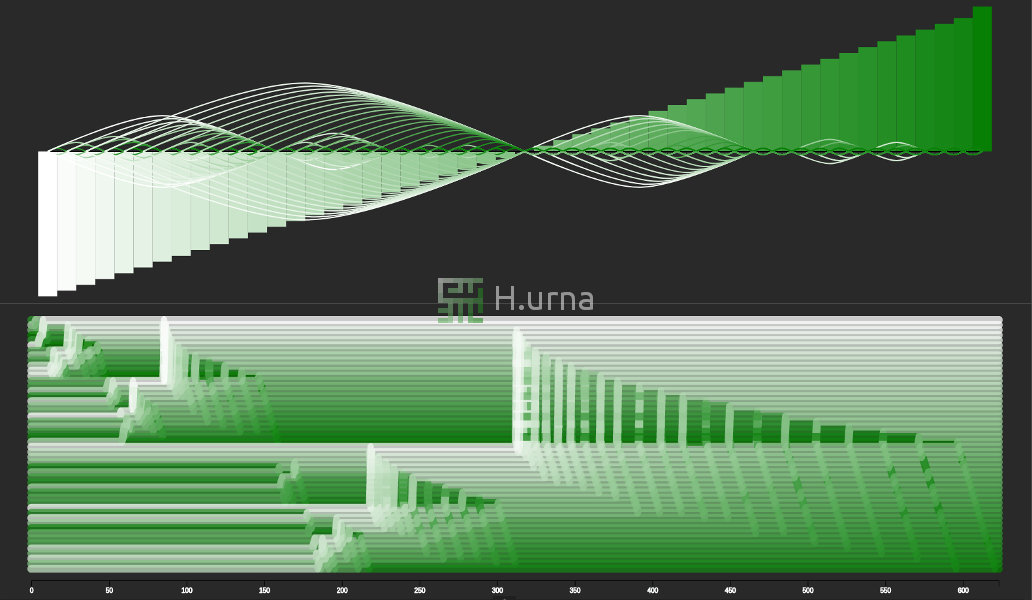
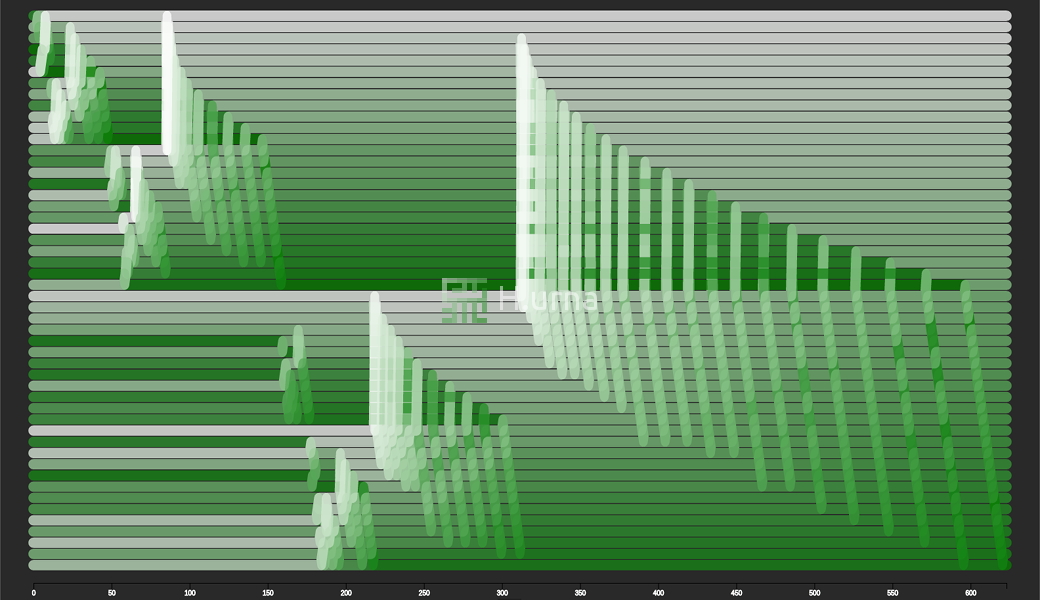
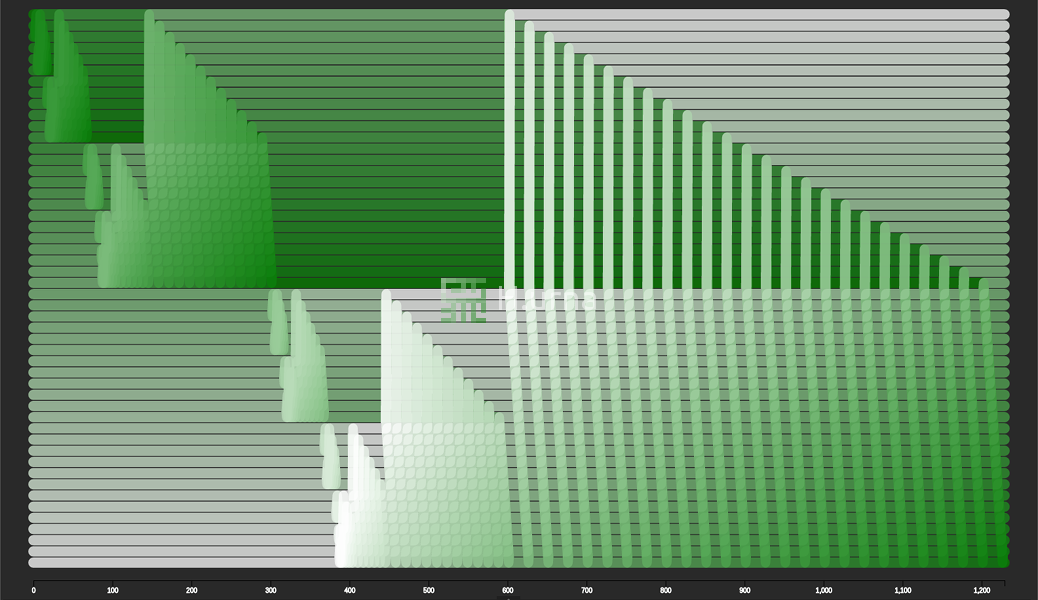
Merge Sort here works in-place following a bottom-up strategy. Initially, it merges two sub-sequences of size one, since these are trivially sorted. Each adjacent sub-sequence (just a pair of elements initially) is merged/aggregated, into a sorted sequence containing both. It then recurses up until the entire sequence got merged.
Steps
- 1. Pick the middle of the sequence.
- 2.a. Recurse on the left side.
- 2.b. Recurse on the right side.
- 3. Merge both sequences.
Code
void MergeSort(Iterator begin, Iterator end)
{
const auto size = distance(begin, end);
if (size < 2)
return;
auto pivot = begin + (size / 2);
// Recursively break the vector into two pieces
MergeSort(begin, pivot);
MergeSort(pivot, end);
// Merge the two pieces
Merge(begin, pivot, end);
}
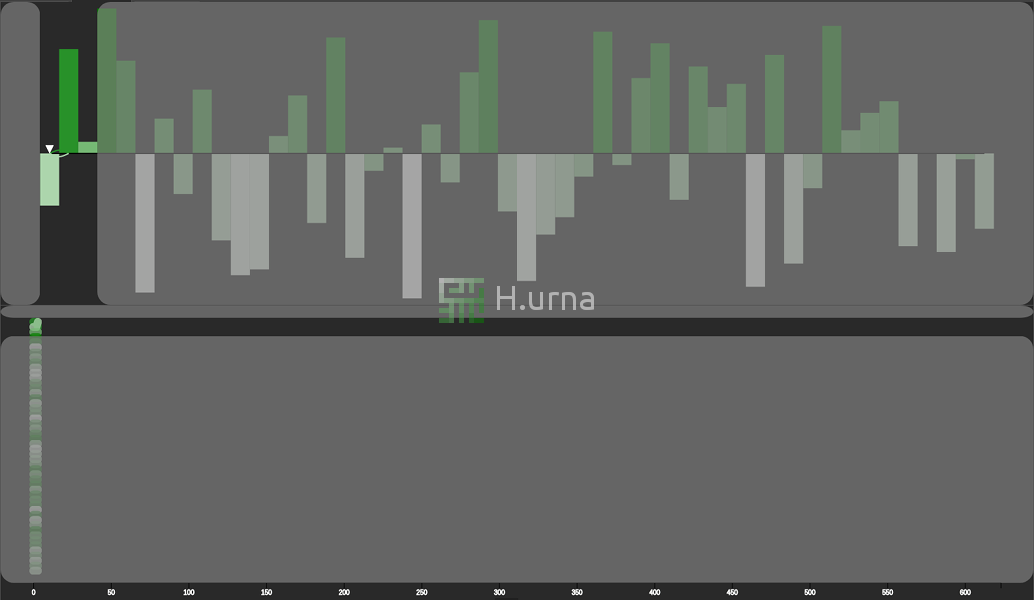
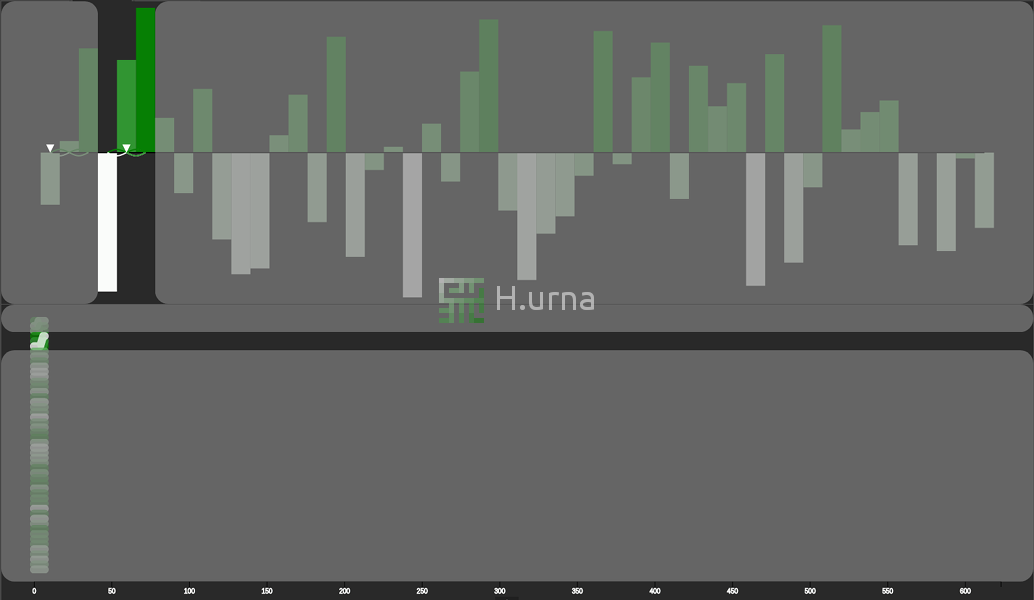
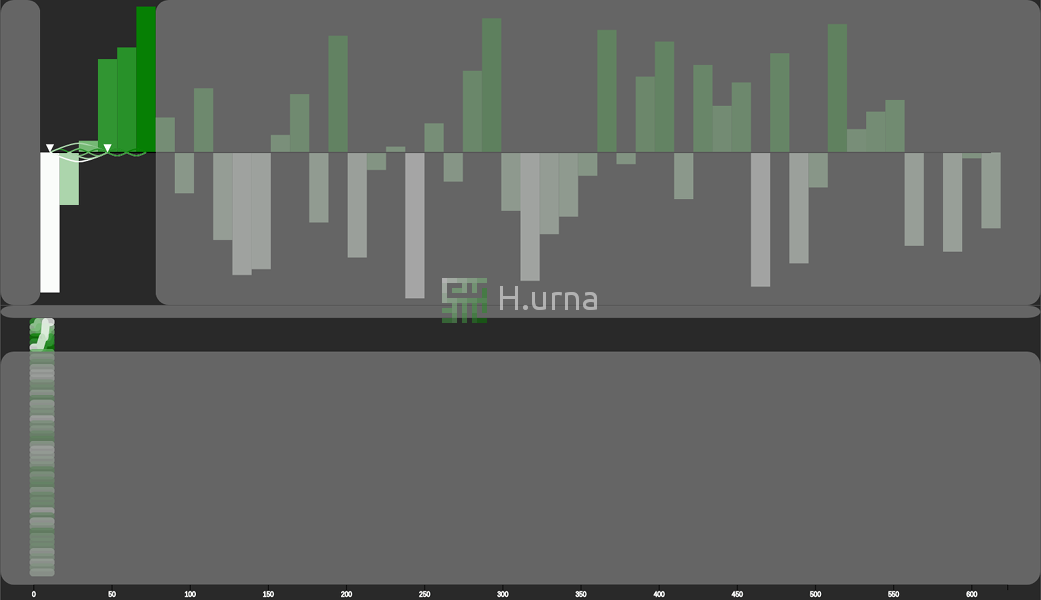
Visualization
Complexity
Reminder
The in-place version of an Aggregate/Merge has a time complexity of:
- O(n/2) ~ O(n) in best case here (m = n/2)
- O(n2/2) ~ O(n2) in worst case here (m = n/2)
- The space complexity of O(1) in all case
Master Theorem for Divide and Conquer Recurrences
$$T(n) = O(n) + 2T(\frac{n}{2}) \quad-->\quad O(n log n)$$Time
Best
The best configuration occurs when all elements are already sorted or nearly sorted. This means that each Merge/Aggregation will behave as an O(n) algorithm. Thus, let us put this into a recurrence relation: $$T(n) = O(n) + T(\frac{n}{2}) + T(\frac{n}{2})$$ $$T(n) = O(n) + 2T(\frac{n}{2})$$ Using the master theorem for divide-and-conquer recurrences: O(n log n).
Average / Worst
The worst case O(n2) occurs when all elements of the first sequence are higher than all elements of the second one during mergings (cf. aggregate in place). Putting this into a recurrence relation: $$T(n) = O(n) + T(\frac{n^2}{2}) + T(\frac{n^2}{2})$$ $$T(n) = O(n) + 2T(\frac{n^2}{2})$$
Using the master theorem for divide-and-conquer recurrences: O(n2).
Space
As a reminder: - In-place aggregation requires O(1) space. - Recursions are made one after on other. This is called tail recursion, meaning the right operates after the left has finished recursion. It implies that the right computation does not add to the left computation call stack.
In this case, the notion of "in-place" can be relaxed to mean "taking logarithmic stack space", which is the amount of space required by the call stack usage.
Parallelization
Due to it being a bottom-up divide and conquer algorithm the work can be easily split up and worked on using different threads, a beneficial trait for high performance systems with large amounts of data.
The parallelism process is as simple as forking both merge sort recursion and joining both at the merge/aggregate process:
void MergeSort(Iterator begin, Iterator end)
{
const auto size = distance(begin, end);
if (size < 2)
return;
// Fork both sequence
auto pivot = (begin + end) / 2;
thread thread1 = MergeSort(begin, pivot);
thread thread2 = MergeSort(pivot, end);
// Join them
thread1.join();
thread2.join();
// Merge the two pieces
Merge(begin, pivot, end);
}



 Play online
Play online
 C++ Source Code
C++ Source Code