Accès Rapide
Introduction
Sur un ordinateur, tout repose en quelque sorte sur des algorithmes. Chaque algorithme prend du temps et de l'espace à exécuter. La complexité algorithmique de ce code est une estimation de cet espace / temps nécessaire à son exécution. Plus la complexité est faible, meilleure est l'exécution.
La complexité, ou la notation Big O, nous permet de pouvoir comparer des algorithmes sans les mettre en œuvre ou les exécuter. Cela nous aide à concevoir des algorithmes efficaces et c'est pourquoi tous les entretiens techniques d'embauche posent des questions sur la complexité algorithmique.
La complexité est une estimation asymptotique. Il s'agit d'une mesure de la façon dont un algorithme évolue en fonction de la taille des entrées, pas d'une mesure de performance spécifique.
Objectifs
Comprendre comment les performances des algorithmes sont calculées. Estimer le temps ou l’espace requis par un algorithme. Identifier la complexité d'une fonction. Ne pas oublier que Big O est une mesure asymptotique et reste floue.
Et ensuite ?
Nous serons beaucoup plus confiants pour aller plus loin avec des structures de données plus complexes (arbre binaire, hash map, etc.) et explorer des implémentations d'algorithmes tels que les tris ou les générateurs de labyrinthes.
Temps d'exécution courants
Voici une image générale des temps d'exécution couramment utilisés lors de l'analyse d'un algorithme : c’est une excellente image à garder à l’esprit chaque fois que nous écrivons du code.
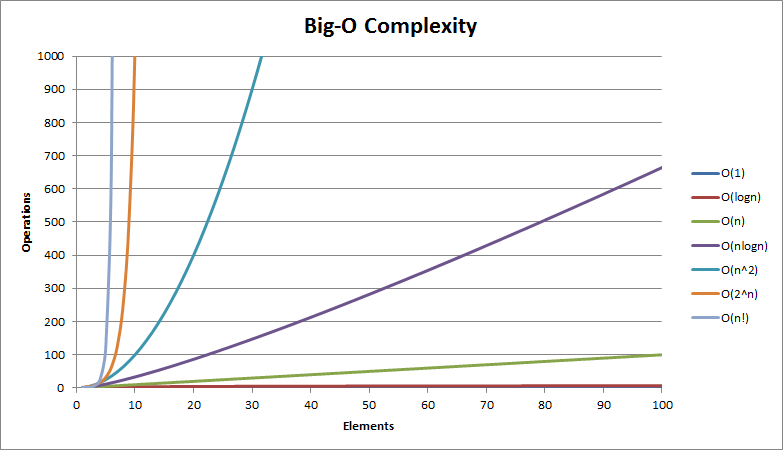
Le graphique montre le nombre d'opérations effectuées par un algorithme en fonction du nombre d'éléments en entrée. On peut voir à quelle vitesse un algorithme peut être pénalisé par sa complexité.
La complexité d'un algorithme dépend évidemment en partie du problème qu'il résout. Voyons ci-dessous les temps courants et certaines implémentations d'algorithmes correspondantes.
Constant - O(1)
O(1) signifie que le temps d'exécution est constant : c'est aussi rapide que la lumière quelle que soit la taille de l'entrée ! Cela concerne la plupart des opérations de base que nous aurons avec n’importe quel langage de programmation (par exemple, affectation de variable, arithmétique, comparaisons, accès aux éléments d’un tableau, échange de valeurs, etc.).
auto a = -1; // O(1)
auto b = 1 + 3 * 4 + (6 / 5); // O(1)
auto d = swap(a, b); // O(1)
if (a < b)
auto c = new Object(); // O(1)
auto array = {1, 2, 3, 4, 6}; // O(1)
auto i = array[4]; // O(1)
...
Logarithmique - O(log n)
Ce sont les types d'algorithmes les plus rapides lorsqu'ils dépendent de la taille des données d’entrée. L'algorithme le plus connu et facile à comprendre avec cette complexité est la recherche dichotomatique dont le code est indiqué ci-dessous.
Index BinarySearch(Iterator begin, Iterator end, const T key)
{
auto index = -1;
auto middle = begin + distance(begin, end) / 2;
// While there is still objects between the two iterators and no object has been foud yet
while(begin < end && index < 0)
{
if (IsEqual(key, middle)) // Object Found: Retrieve index
index = position(middle);
else if (key > middle) // Search key within upper sequence
begin = middle + 1;
else // Search key within lower sequence
end = middle;
middle = begin + distance(begin, end) / 2;
}
return index;
}
Communément : les algorithmes de stratégie diviser pour régner peuvent avoir une complexité logarithmique.
Linéaire - O(n)
La durée d'exécution augmente linéairement avec la taille de l'entrée : si la taille en entrée est n, l'algorithme effectuerait également n opérations tout au plus. Le temps linéaire est la meilleure complexité possible dans les situations où l'algorithme doit lire séquentiellement toutes les entrées.
Prenons l'exemple où nous devons calculer la somme des gains et des pertes (gain total). Bien sûr, nous devrons examiner chaque valeur au moins une fois :
T Gain(Iterator begin, Iterator end)
{
auto gain = T(0);
for (auto it = begin; it != end; ++it)
gain += *it;
return gain;
}
Si nous avons une boucle for unique avec des données simples, il en résulte très probablement une complexité en O(n).
Quasi Linéaire - O(n log n)
Les algorithmes en O(n log n) sont légèrement plus lents que ceux en O(n). C’est par exemple la meillure complexité temporelle liée aux algorithmes de tri.
Dans de nombreux cas, la complexité en O(n log n) est simplement le résultat de l'exécution d'une opération logarithmique n fois ou vice versa. A titre d'exemple, l'algorithme de tri par fusion classique :
void MergeSort(Iterator begin, Iterator end)
{
const auto size = distance(begin, end);
if (size < 2)
return;
auto pivot = begin + (size / 2);
// Recursively break the vector into two pieces
MergeSort(begin, pivot); // O(log n)
MergeSort(pivot, end); // O(log n)
// Merge the two pieces - considered to be in O(n)
Merge(begin, pivot, end); // O(n)
}
Ils sont souvent le résultat d’optimisations à partir d’un algorithme en O(n2).
Quadratique - O(n2)
C'est le genre de complexité régulièrement rencontré. Ces algorithmes surviennent souvent lorsque nous voulons comparer chaque élément avec tous les autres. Le tri à bulles, un algorithme généralement étudié, illustre parfaitement ce temps d'exécution. Voici sa version la plus naïve:
void BubbleSort (Iterator begin, Iterator end)
{
// For each pair of elements - bubble the greater up.
for (auto it = begin; it != end; ++it)
for (auto itB = begin; itB < end; ++itB)
if (Compare(itB, (itB + 1))) swap(itB, (itB + 1));
}
Si vous avez une double boucle for (imbriquées) avec des données simples, il en résulte très probablement une complexité en O(n2).
Exponentiel - O(2n)
Commence ainsi le type d'algorithmes très gourmands. Généralement, la complexité n2 est acceptable tandis que 2n est presque toujours inacceptable. L'implémentation de l'algorithme de fibonacci récursive en est l'exemple le plus connu.
int Fibonacci(int n)
{
if (n <= 1)
return 1;
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
Pour voir à quelle vitesse le temps d'exécution peut devenir inacceptable : - 5 elements --> 32 opérations - 10 elements --> 1024 opérations - 100 elements --> 1,2676506×10³⁰ opérations !
Néanmoins, pour certains problèmes nous ne pouvons pas atteindre une meilleure complexité. C'est par exemple le cas du problème du voyageur de commerce qui peut atteindre cette complexité grâce à des optimisations de programmation dynamiques.
Factoriel - O(n!)
C'est le plus lent de tous et est considéré comme impraticable. La plupart du temps, nous n'aurions pas à traiter avec de tels algorithmes.
C'est par exemple le cas du problème du voyageur de commerce via la recherche par force brute : il essaie toutes les permutations et recherche quelle est la moins chère en utilisant la force brute.
Maths
Pour ne pas être trop long et ennuyer la plupart des lecteurs, nous ne ferons que mettre quelques égalités mathématiques utiles comme rappel pour ceux qui veulent aller plus loin avec le calcul de la complexité.
| Sommes Mathématiques | Master Theorem for Divide and Conquer Recurrences |
|---|---|
| $$\sum_{i=0}^{n-1} {C}^{ste} = n * {C}^{ste}$$ | $$T(n) = O(n) + 2T(\frac{n}{2}) --> O(n log n)$$ |
| $$\sum_{i=0}^{n-1} n = n(n-1)$$ | $$T(n) = O(1) + T(\frac{n}{2}) --> O(log n)$$ |
| $$\sum_{i=0}^{n-1} i = \frac{n(n + 1)}{2} - n = \frac{n(n - 1)}{2}$$ | |
| $$\sum_{i=0}^{n-1} (n+i) = \sum_{i=0}^{n-1} n + \sum_{i=0}^{n-1} i$$ |
Assymptotiques du nombre harmonique généralisé Hn,r:
$$H_{n,r} = \sum_{k=1}^{n} \frac{1}{k^r}$$ $$For \quad n \approx 1$$ $$H_{n,1} \in O(log(n))$$

 O(1)
O(1)
 O(log n)
O(log n)
 O(n)
O(n)
 O(n log n)
O(n log n)
 O(n2)
O(n2)
 O(2n)
O(2n)
 O(n!)
O(n!)
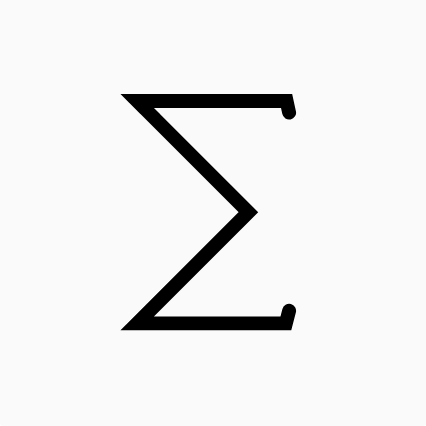 Maths
Maths