Beaucoup pensent que les équations et l'algèbre sont difficiles, obscures et ésotériques. En réalité les équations sont des concepts relativement simples. En connaissant les règles de base du jeu et avec un petit peu de pratique, vous pouvez apprendre à les manipuler et à les résoudre en un clin d'œil.

Les équations linéaires sont la forme d’équation la plus simple. Elle limite le problème à une seule variable inconnue (généralement appelée x) et ne contient aucun exposant (par exemple x - 30 = 15).

La forme générale d'une équation linéaire (après avoir tout déplacé du côté gauche) est la suivante: $$\textbf{ax + b = 0}$$ Avec a et b deux nombres fixes (ceux que vous voulez ^^).

Nous résolvons inconsciemment ce genre d’équation tous les jours.
Disons que nous sommes à l'entrainement (de sport), le chrono a été lancé depuis 30 minutes, et l’entraîneur nous annonce encore 15 minutes de course.
Combien de temps allons-nous courir au total ? Ce problème peut être écrit comme suit:

$$?TempsTotal? - TempsCouru = TempsRestant$$ $$x - 30 = 15$$

Vous avez peut-être déjà le résultat en tête, mais jouons le jeu de l'algèbre:
$$TempsTotal = TempsCouru + TempsRestant = 30 + 15 = 45 Minutes$$

Nous savons alors avec certitude que nous allons courir 45 minutes au total (sauf si l'entraîneur nous ment). Voyons maintenant toutes les règles du jeu. Vous verrez, il y en a assez peu (même pour résoudre des problèmes plus complexes) !

Le Jeu

Objectif

Une équation est comme une affirmation disant "ceci est égal à cela". L’équation précédente, x - 30 = 15, pose la question suivante : Combien vaut x pour rendre cette affirmation vraie ?

Le but est donc de trouver x. Dans le monde algébrique, c'est arriver à :
x = quelque chose sans x .

La prochaine partie vous présente les règles et les outils utiles pour atteindre cet objectif. N'oubliez pas que résoudre une équation revient à résoudre une énigme : il y a des choses que nous pouvons faire et d'autres qui nous sont interdites.

Règles

Il y a seulement deux règles à satisfaire:

Quoi que vous fassiez d'un côté de l'équation, vous devez le faire de l'autre côté pour garder la balance équilibrée.

Il est interdit de diviser quoi que ce soit par 0 !

Outils

Basiques

Fractions

Exemple de résolution détaillée

Vérifier la solution

L'idéal et l'important est de toujours vérifier que votre "solution" est vraiment une solution. Pour cela, rien de plus facile: Remplacez x par la valeur de la solution dans l’équation et vérifiez que l’égalité est vraie.

Attention à ce que votre solution ne divise jamais par 0 !

Dans l'exemple précédent, nous avons trouvé x = 45. Si nous le plaçons dans l'équation, nous obtenons: $$45 - 30 = 15$$ Ce qui est vrai: la solution a été vérifiée.

La méthode toujours gagnante

Ce n’est pas la manière optimale, mais vous êtes sûrs de toujours atteindre l'objectif en utilisant cette méthode ! Voici comment procéder :

Est-ce que l'équation a des fractions ?
Oui → Multiplier chaque terme (des deux côtés) par le dénominateur à éliminer.

L'équation contient elle des parenthèses ?
Oui → Développer l'équation à l'aide des outils.

Y a-t-il des termes similaires de chaque côté de l'égalité ?
Oui → Combiner les mêmes termes. (Ne pas oublier le signe devant chaque terme!)

Y a-t-il x des deux côtés de l'équation?
Oui → Ajoutez ou soustrayez les termes pour obtenir tous les x du côté gauche et toutes les constantes du côté droit.

À ce stade, il ne doit plus rester qu'une étape (sinon, il y a eu une erreur).

Multiplier ou diviser pour supprimer les coefficients du côté gauche de l'équation.

!SOLUTION TROUVÉE!

Ne pas oublier de vérifier sa solution ! :).

Equations et Représentations Graphiques

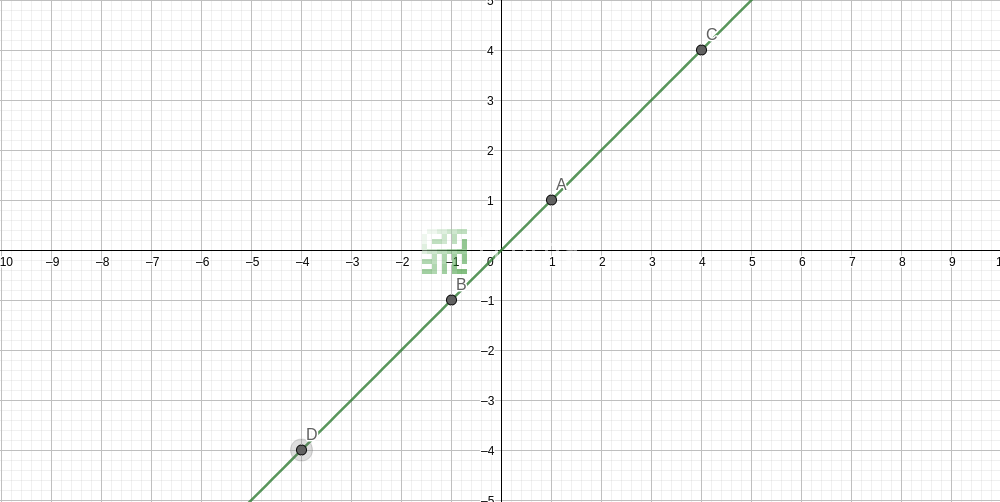
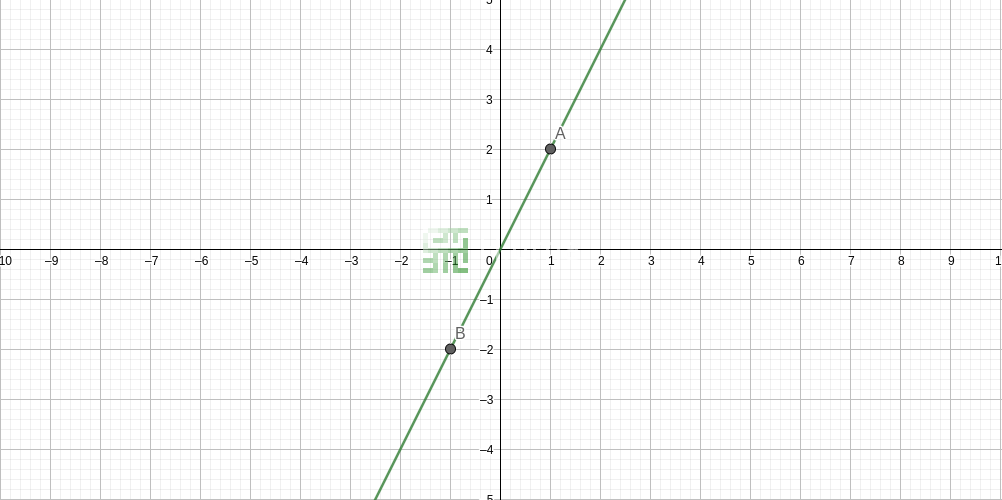
Toute expression linéaire (la partie gauche ou droite d'une équation) peut être représentée sous la forme d'une ligne dans un graphique 2D.
Le dessin graphique est très simple : pour chaque partie de l'équation, nous avons y sur l'axe vertical (le résultat) et pour une plage de valeurs de x (axe horizontal), nous calculons et dessinons les points (x, y).

La ligne la plus simple, y est constant : y=-3 (quelque soit x : y = -3).

L'autre ligne à connaitre : y=x (quelque soit x : y a la même valeur que x).

Ici y = 2x
Multiplier x par une constante, c'est faire une rotation sur la ligne.

Une forme complète avec y = 2x - 3
Ajouter ou soustraire par un nombre constant revient à ajouter un offset (déplacement vertical).

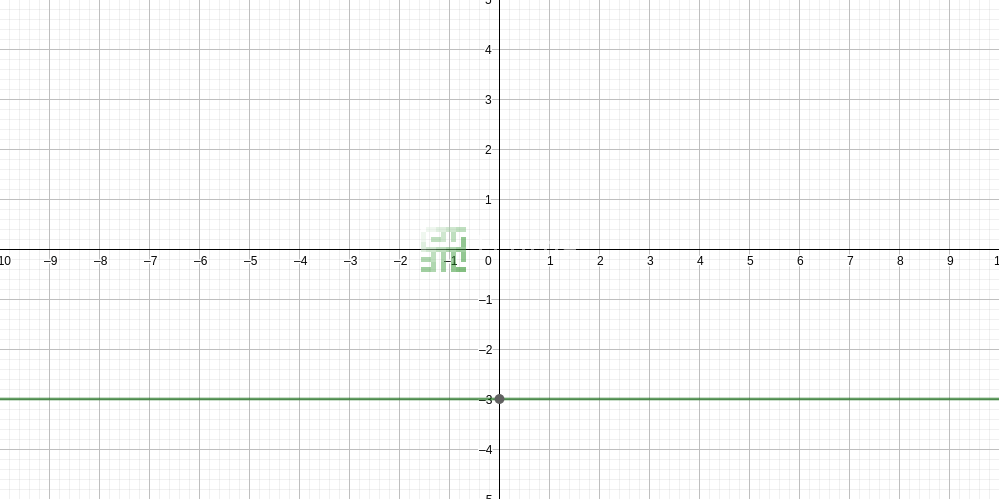
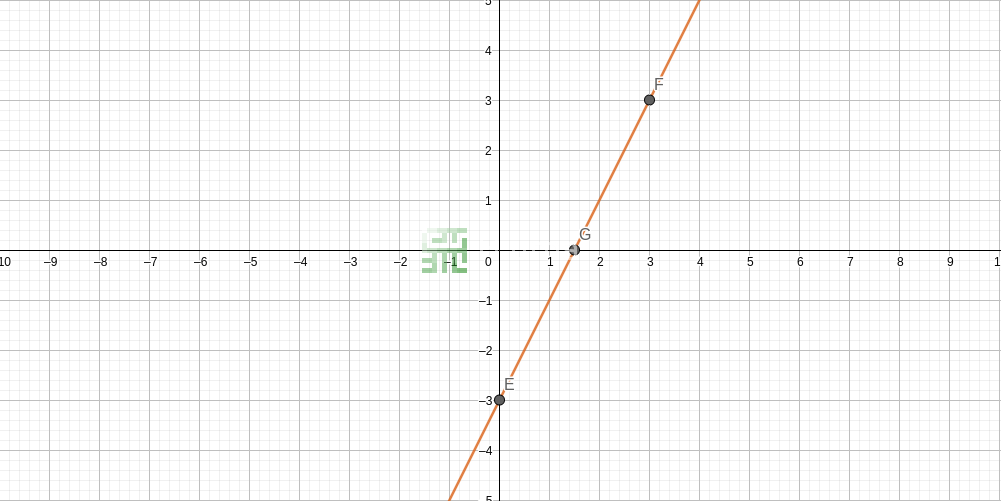
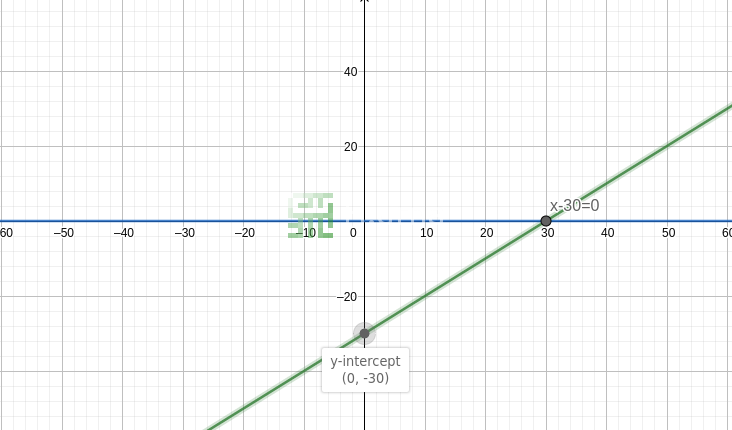
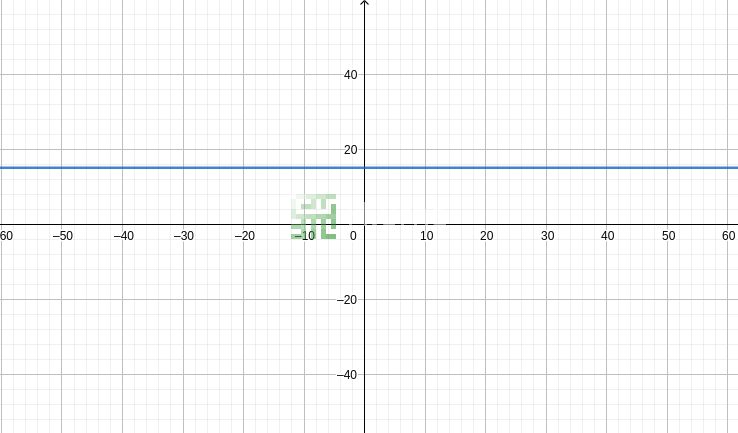
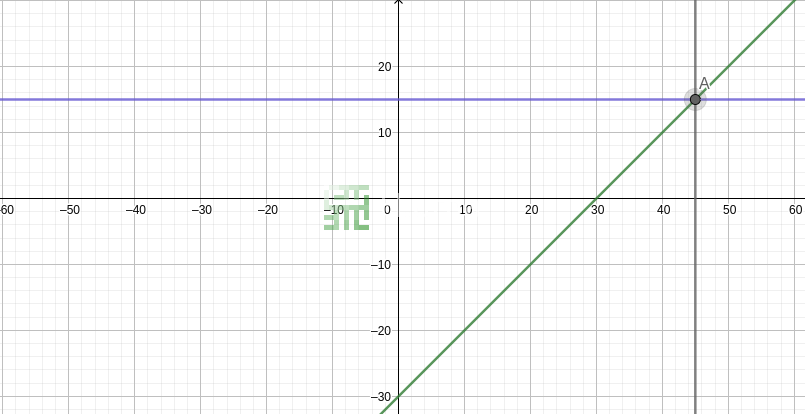
Une équation linéaire peut être dessinée sous la forme de deux lignes se croisant (une ligne pour la partie gauche de l'équation et une autre pour celle de droite). Le point d'intersection de ces deux lignes est la solution d'équation (si les lignes sont parallèles, cela signifie que l'équation n'a pas de solution). Comme dans le monde algébrique, la question répond à : quel est x qui rendra cette équation vraie, quand est-ce que ces lignes ont le même y ou se croisent elles ?

Avec notre équation, x - 30 = 15, calculons quelques points :

Partie gauche : y = x - 30

Partie droite : y = 15

Les deux ensemble avec la solution de l'intersection : x = 45.

L’avantage de dessiner les lignes d’une équation est de pouvoir visualiser directement la valeur de y pour chaque x, ou bien de x pour chaque y.

Nous avons ici illustré la relation entre une équation algébrique et sa représentation graphique; cela vous offre une autre façon de jouer avec les équations.

Sautez à bord de l' H.urna Explorer pour voir et résoudre vos équations.