H.urna - Use senses to learn sciences

H.urna is currently under reconstruction. Thank you for your patience.

  1. Academy
  2. Mathematics
  3. Linear Equations

Quick Access

H.urna Explorer - Discover and manipulate a linear model on the graph Play online

Automatic solver and visualizer like a teacher would explain Step-by-step Solver

Solving Linear Equation

Many people think that equations and algebra are obscure and use some esoteric languages. The truth is that equations are relatively simple concepts; knowing the base rules of the game and a bit of practice, you can learn to manipulate and solve them in a snap.

A linear equation is the simplest form of the equation you may deal with; it restricts the problem to a single unknown variable (usually called x) and no exponent (e.g. x - 30 = 15).

The general form of such equation (after moving everything on the left side) is: $$\textbf{ax + b = 0}$$

We all have solved this kind of equation every day even without even notifying it. Let us say we are currently getting training, we know it has been 30 minutes I am running and the coach told us that we remain 15 minutes running. How much are we going to run in total? This problem can be written as the following:


$$?TotalTime? - TimeAlreadyRun = TimeLeft$$ $$x - 30 = 15$$


The result may already be solved, here is the equation game:
$$TotalTime = TimeAlreadyRun + TimeLeft = 30 + 15 = 45 Minutes$$


We know for sure we are gonna made a total 45 minutes run (except if the coach is playing on us). Now let us have a peek to the rules of the game, you will see: there is quite a few (even with the most complex problems)!

Rules of the Game

Goal

An equation is like a statement saying "this equals that”. The previous equation, x - 30 = 15 asks: what x will make makes this equation true?

The goal is thus to find that x; in the algebraic world, meaning to end up with:
x = something without x.

Next part presents you the rules and useful tools dedicated to reaching this goal. Keep in mind that solving an equation is just like solving a puzzle: there are things we can do and some others that are forbidden.

Rules

There are only two rules to satisfy:

Whatever you do to one side of the equation, you must do to the other side.
You are forbidden to divide anything by 0.

Tools

Basics

  • $$a*0=0$$
  • $$-(a+b)=-a-b$$
  • $$-(-a)=a$$
  • $$(a+b)(c+d)=ac+ad+bc+bd$$
  • $$a*1=a$$
  • $$-(a-b)=-a+b$$
  • $$a(b+c)=ab+ac$$

Fractions

  • $$\frac{0}{a}=0\:,\:a\ne 0$$
  • $$\frac{a}{a}=1$$
  • $$\frac{-a}{b}=-\frac{a}{b}$$
  • $$\frac{a}{\frac{b}{c}}=\frac{a\cdot c}{b}$$
  • $$\frac{1}{\frac{b}{c}}=\frac{c}{b}$$
  • $$\frac{a}{1}=a$$
  • $$\frac{-a}{-b}=\frac{a}{b}$$
  • $$\frac{a}{-b}=-\frac{a}{b}$$
  • $$\frac{\frac{b}{c}}{a}=\frac{b}{c\cdot a}$$

Example of detailed resolution

Math Logger Visualizer

Check our solution

We should always check that our "solution" is a solution; there is nothing easier: Replace ‘x' by the solution value within the equation and verify that the equality is true.

Be careful to check that your solution never divides by 0!

In the previous example we found x = 45. If we place it within the equation, we get: $$45 - 30 = 15$$ Which is true: the solution has been verified.

The always winning method

It is not the optimal way, but the always winning robot always reach the goal using this method! Here is how he proceeds:

Does the equation have fractions?
Yes → Multiply every term (on both sides) by the denominator.

Does the equation involve parenthesis?
Yes → Expand the equation using the tools.

On either side, does it have like terms?
Yes → Combine like terms. (Do not forget the sign in front of each term!)

Does it have variables on both sides of the equation?
Yes → Add or subtract the terms to get all the variables on the left side and all the constants on the right side.

At this point, the robot has a basic two-step equation (If not, he would be bugged).

Add or Subtract to remove any constants from the left side of the equation.
Multiply or Divide to remove any coefficients form the left side of the equation.

!SOLUTION FOUND!



In the end, the robot does not forget to check its answer to detect any future problem :).

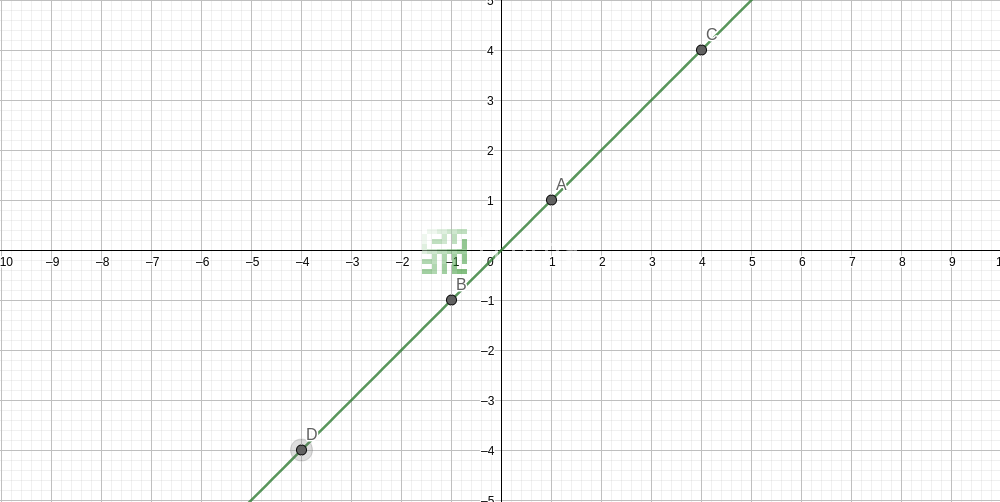
Equations and Graph Representation

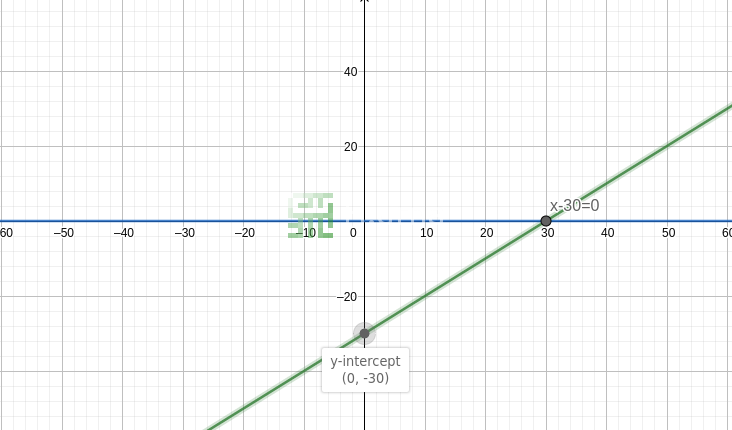
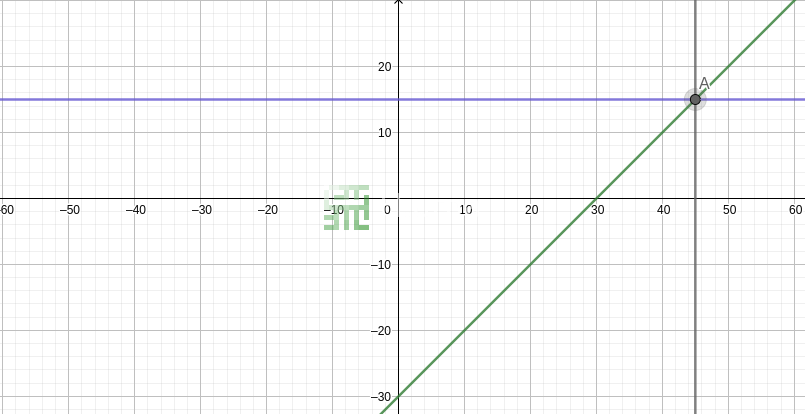
Any linear expression (the left or right part of an equation) can be drawn as a line in a 2D graphic. The graph drawing is straightforward: we have y on the vertical axis (the result) and for a range of x values (horizontal abscissa) we compute and plot the points (x, y).



A linear equation can be then drawn as two lines crossing each other. The intersection point of those two lines is the equation solution (if the lines are parallel, it means that the equation does not have any solution). Indeed the question answer the same one from the algebraic world: What x will make makes this equation true: when those lines are equal?

With our previous equation, x - 30 = 15, let's compute ourselves few points composing the lines:

x Left part equation line Result (x - 30) Right part equation line Result (15)
  • $$x=-15$$
  • $$x=0$$
  • $$x=15$$
  • $$x=30$$
  • $$x=45$$
  • $$y = -15 -30 = -45$$
  • $$y = 0 - 30 = -30$$
  • $$y = 15 - 30 = -15$$
  • $$y = 30 - 30 = 0$$
  • $$y = 45 - 30 = 15$$
  • $$point(-15, -45)$$
  • $$point(0, -30)$$
  • $$point(15, -15)$$
  • $$point(30, 0)$$
  • $$point(30, 15)$$
  • $$y = 15$$
  • $$y = 15$$
  • $$y = 15$$
  • $$y = 15$$
  • $$y = 15$$
  • $$point(-15, 15)$$
  • $$point(0, 15)$$
  • $$point(15, 15)$$
  • $$point(30, 15)$$
  • $$point(30, 15)$$



The advantage of drawing a graph of an equation is that you can then use it to visualize out the value of y for any given value of x, or indeed x for any given value of y.

We have illustrated here the relationship between an algebraic equation and its graph plots giving you an alternative way to understand equations.

Jump in Hurna Explorer to practice and visualize yourself any equations.