Contrairement à la pente d'une droite linéaire qui est constante (coefficient directeur), celle d'une courbe change constamment tout au long du graphique. Imaginez-vous en train de vous préparer pour une longue randonnée en montagne: la courbe est la montagne elle-même et nous voulons savoir quelles seraient les pentes à gérer et quand nous pourrions nous arrêter pour faire notre campement (espérant un endroit sans trop de pente pour être plat).

Pour obtenir cette fonction de pente (description de son évolution), les mathématiques ont l’un de leurs plus merveilleux outils : la dérivation. Cette dérivation est utilisée pour trouver la dérivée d’une fonction et cette dérivée, notée f’(x), est la fonction qui décrit exactement l’évolution de la pente ! La dérivation est utilisée pour trouver des tonnes de choses telles que les extrema d’une fonction, la desccription des trajectoires (quand et comment évoluent les vitesses, les accélérations...) et nous sommes ravis d’écrire un cours complet à ce sujet sous peu.

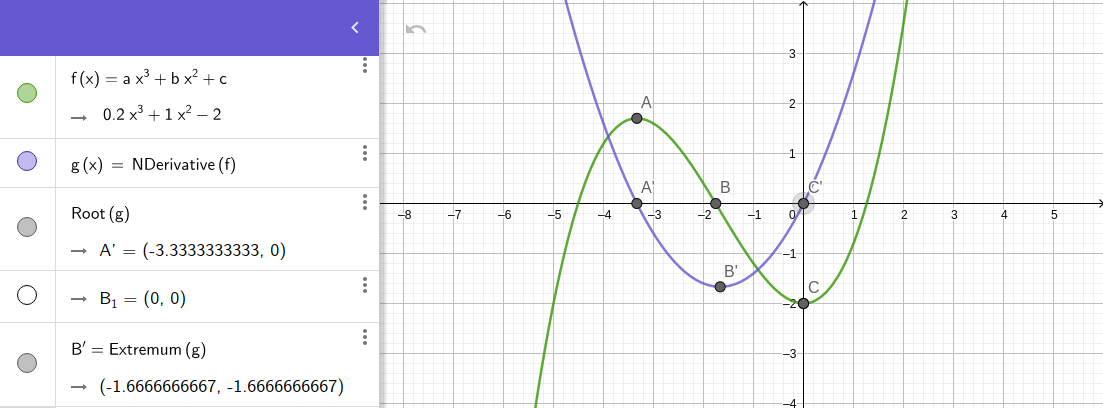
Montre une courbe f(x) en vert (la montagne) et son évolution de la pente f’(x) en bleu (la dérivée) :
$$f(x) = 0.2x^{3} + x^{2} - 2$$ $$f’(x) = 0.6x² + 2x$$

L’évolution de la pente se lit directement au fil de l’évolution de notre fonction, ce qui est très pratique !
Nous pouvons voir en quelques secondes les informations suivantes :
- A est un extrema, lorsque la pente de f est égale à 0 (c’est plat).
- A’ est son point sur sa dérivée (comme la pente, f’(a) = 0)
- B ’est le point où f’ est au minimum: c’est là que la pente descend le plus vite.
- Sur C, C’ on voit le deuxième extrema : mêmes observations que pour A, A’.

Notre calculatrice graphique calcule et trace automatiquement notre dérivée, c’est un outil extraordinaire pour visualiser et vérifier la solution de nos problèmes.