75x50 Maze generated by a Sidewinder algorithm (Top-Left flooding).

Flooding starting from Top-Left corner.

The tree representing its data structure topology from Top-Left corner.

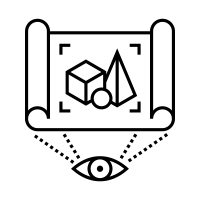
Sidewinder Maze Generator is very similar to the Binary Tree algorithm, and only slightly more complicated. Furthermore, the Sidewinder algorithm only needs to consider the current row, and therefore can be used to generate infinitely large mazes (like the Binary Tree).

While binary tree mazes have two of its four sides being one long passage, a Sidewinder mazes have just one long passage.

while it is related to the Binary Tree algorithm, it is a bit more complicated. However, words do not do it justice; it is a lot more straightforward than it sounds.

Steps

• For each row in the grid:
• 1. For each cell randomly decide whether to carve a passage leading East
• a. If the passage is carved add the cell to the current run set
• b. If the passage is not carved, randomly pick one cell from the route set, carve a passage leading North and empty the current run set

Code

Maze Sidewinder(int width, int height)
{
  Maze maze(width, height);

  // First row can only be a single passage (cannot crave north), crave it.
  for (auto x = 0; x + 1 < width; ++x)
    maze[x][0]->Connect(maze[x + 1][0]);

  // Scan grid row by row (starting from the second one)
  for (auto y = 1; y < height; ++y)
  {
    // Initialize an empty “run” set to keep track of the current run path
    Set runSet;

    for (auto x = 0; x < width; ++x)
    {
      // Add current cell to the path
      runSet.insert(maze[x][y]);

      // Randomly carve to east (if possible) or not
      if ((x + 1) < width && Random() % 2)
      {  mazeMatrix[x][y]->Connect(mazeMatrix[x + 1][y]); }
      // Otherwise carve to the north from a random cell of the run set
      else
      {
        auto cell = runSet.GetRandom();
        cell->Connect(cell{y -= 1});

        // Empty the run set and continue row scan
        runSet.clear();
      }
    }
  }

  return maze;
}

Any maze generated by the Sidewinder algorithm will never have any North-facing dead-ends, which means you can never get stuck when moving from South to North. This is similar to the Binary Tree algorithm, which will never have any dead-ends in the direction of its bias.

A sidewinder Maze tends to have an elitist solution, where the East path is straightforward, but many long false paths are leading down from North path next to it.

The solution is deterministic without error from bottom to top: it will never double back on itself or visit a row more than once, although it will wind (or wave) from side to side.

1. First row can only be a single passage (cannot crave north).

2. First cell decides to carve East, carve and add it to runSet.

3. Second cell decides the runset to carve North, it randomly select itself to carve.
runSet is cleared.

4. Next two cells decide to carve East.

5. The last one of the row has to carve a passage North from the runSet. It choose the first one (of the runSet) to be the one carving.

6. Few rows later...

7. Once all rows has been processed, the maze is generated!