If we understand the Linear and Translate functions above, we may imagine what could be the scaling function : instead of playing with additions, we will play with multiplication factors to stretch or compress our mathematical object. Please note that a scale is a non-rigid transformation : it alters the shape and size of the graph function.

We can stretch or compress it in the y-direction by multiplying the whole function by a constant:
$$f(x) → a * f(x)$$

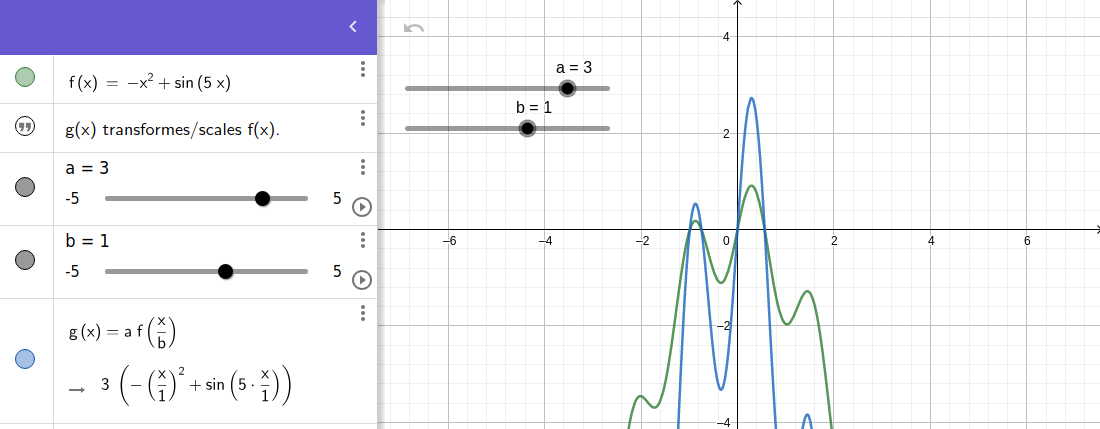
We can stretch or compress it in the x-direction by multiplying the function variable x by a constant:
$$f(x) → f(b * x)$$

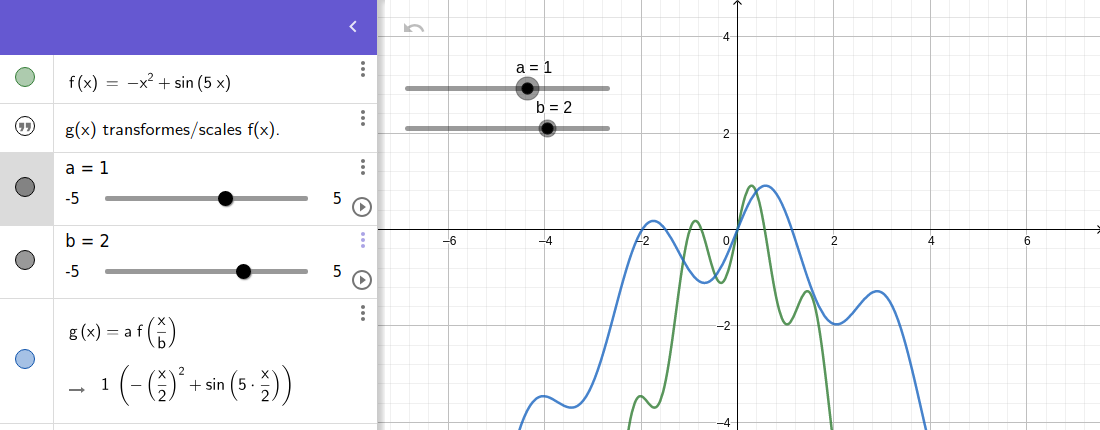
Putting it together :
$$\textbf{f(x) → a * f(b * x)}$$

I am sure we can now imagine why bigger b value causes more compression on the x-scale.
We could say : we put more information within the same base unit.