Just like transformations in geometry, we can translate/shift a mathematical object by changing its function.

Already seen with the previous models (linear, quadratic), we can move it up or down by adding a constant to the function:
$$f(x) → f(x) + b$$

To move it left or right, we add a constant to the function variable (x-value):
$$f(x) → f(x + a)$$ We can think of this as moving the "abscissa origin" to be more in advance or a bit late.

Putting it together:
$$\textbf{f(x) → f(x + a) + b}$$

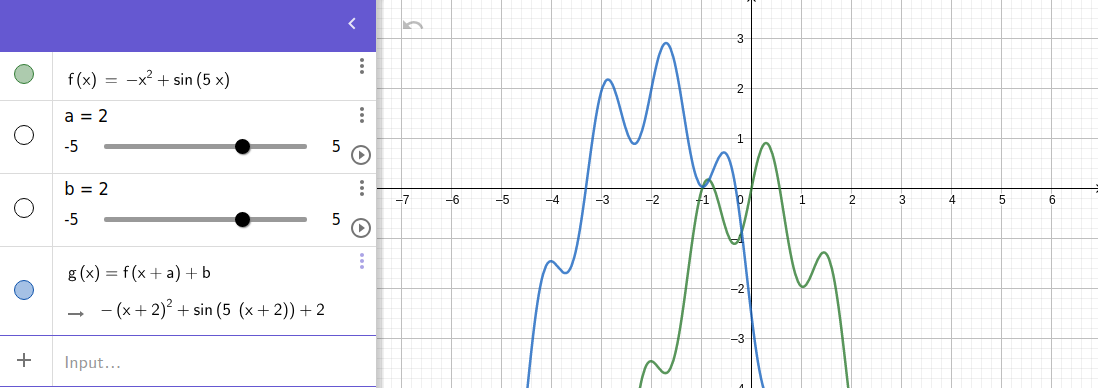
Why adding a positive number a to the variable does move the function to the left (the negative direction)?

Well imagine you want to start recording a movie at 8:00 with the function:
Start(t) = 8:00 o’clock.

If you change your mind to say that we want to record 5 minutes before, we will have the function:
Start(t + 5 mins) = 8:00 o’clock

Adding 5 minutes to the current time will make the record starting 5 minutes earlier (i.e. to the left direction). It is just like putting our watch in advance for an appointment.