In the previous lesson, we have learned about natural, or whole, numbers (0, 1, 2, 3...). It’s now time to enlarge our vision of numbers with integers. Integers are just like whole numbers, but they also include negative numbers: {...-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...}. The set of integers is noted Z.

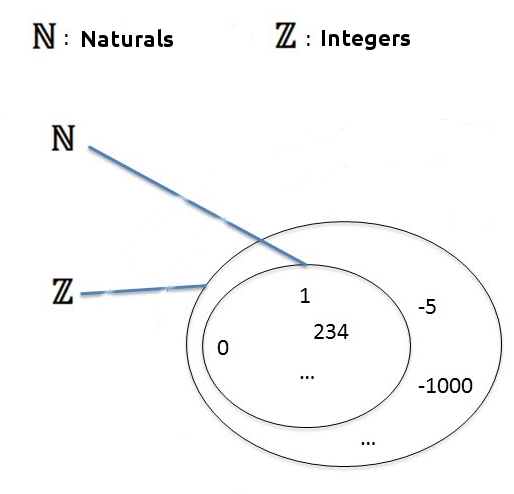
In other words, the set of integers is the union of the set of natural numbers and their opposites. If a is an natural number then -a is an integer of opposite sign. On a graduated axis, two opposite numbers are symmetrical with respect to the origin (0).

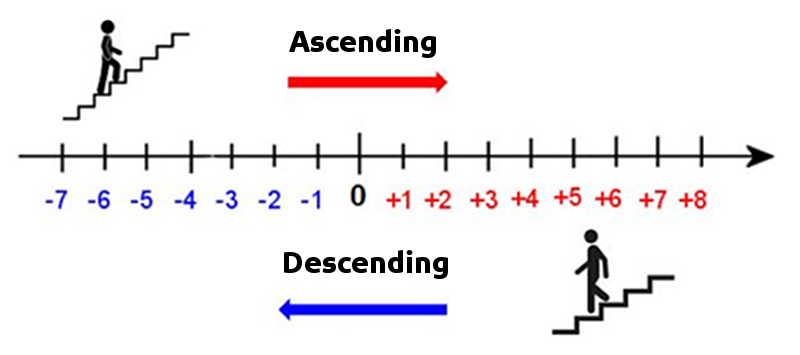
Please note that Zero is considered to be both positive and negative.

Note: Some people may have different definitions for the same word used to define a number set. Some people say that whole numbers can also be negative, which makes them exactly the same as integers. Some people also say that zero is NOT a whole number.

To be precise, the easiest way is to use the mathematical notation. This notation is strict and therefore avoids any confusion:
Z   : all integers.
Z^* : (Z star) all integers except 0 (zero).
Z⁺ : all integers greater or equal to 0. It is the same as N.
Z^*₊ : all integers greater than 0. It is the same as N⁺.

In the 7th century AD, the Indian mathematician BRAHMAGUPTA set out for the first time rules to operate on three kinds of numbers displayed "goods", "debts" and "zero". Debts (somehow negative numbers) were then used in India for trade.

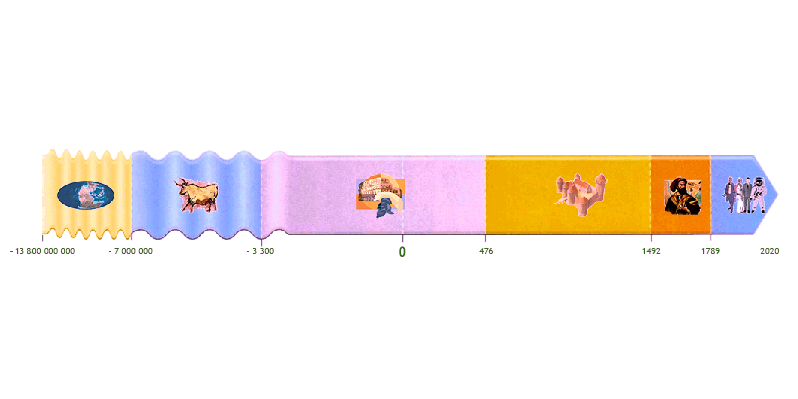
Today we find examples of negative numbers absolutely everywhere:
- Elevator: To go down into the basement we have a “-” sign telling us to go below the ground floor.
- Weather: If the temperature is below 0°, the “-” sign will indicate this negative temperature.
- Video game: When we lose life points, we see on the screen "-" signs in front of the numbers.
- Chronological frieze: A date before our year 0 will be noted with a "-" sign or will be annotated "BC".
- Finance: A bank uses positive numbers to represent deposits and negative numbers to represent withdrawals.
- Etc.

If these negative numbers are used absolutely everywhere today, you should know that they were ignored for a very long time, or even looked down upon as difficult for the human mind to grasp. Here is a little bit of history which will also console all those who encounter difficulties with negative numbers!

A little history

Although the first set of rules for dealing with negative numbers was stated in the 7th century by the Indian mathematician Brahmagupta, it is surprising that in the 18th century, negative numbers were still considered absurd in Europe.

In 1758, the British mathematician Francis Maseres was claiming that negative numbers "... darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple".

Negative numbers aren’t that easy.
What, exactly, do negative numbers mean?
How can you take 4 pens from 3?
How could you have less than nothing?
Yet today, it seems absurd to think negatives aren’t logical or useful.

What happened?
Negatives are not something we can touch or hold.

Things started to change when European scholars started translating Arabic texts obtained from North Africa. They were finally exposed to new ways of thinking, and started catching up with the Indian and Chinese subcontinent.

Rather than saying “I owe you 30″ and reading words to see if I’m up or down, I can write “-30″ and know it means I’m in the hole. The positive and negative signs automatically keep track of the direction — you don’t need a sentence to describe the impact of each transaction.

With the "minus" sign notation Math became easier and more elegant. It didn’t matter if negatives were “tangible” — they had useful properties, and we used them until they became everyday items.

But let’s not be smug about the struggle: negative numbers were a huge mental shift. Even Euler, the genius who discovered exponential and much more, didn’t understand negatives as we do today. They were considered “meaningless” results.

As Bernard de Chartres, Isaac Newton or Blaise Pascal would say:
We are "Dwarfs on the shoulders of giants".

Addition & Subtraction

Good news: these operations are done exactly as for natural numbers !
Except that this time, we can go below 0; please note that ‘-a’ means exactly the same as ‘0 - a’.

There are two unique things to know to quickly become a real ninja in the art of carrying out our operations:

1. Adding a negative is the same as subtracting a positive: $$ \pmb{ (-b) + a = a - b } $$ $$ \pmb{ a + (-b) = a -b } $$

2. Subtracting a negative is the same as adding a positive: $$ \pmb{ a - (-b) = a + b } $$

Let’s take an example that looks complicated and turn it into something very simple:
$$ 5 + 4 - 3 + (-2) - 2 - (-4) = ? $$

Rule 1 : +(-2) → - 2
Rule 2 : -(-4) → + 4

Thus:
$$ 5 + 4 - 3 + (-2) - 2 - (-4) \\= 5 + 4 - 3 - 2 - 2 + 4 \\= 6 $$

And voila! We already know everything about addition and subtraction!

Multiplication & Division

We still have good news!

As for additions and subtractions:
- These operations are done exactly as for natural numbers
- There are two unique things to know.
- The combination of signs results the same.

1. The product of two numbers of opposite sign is negative.: $$ \pmb{ -b * a = - (a * b) } $$ $$ \pmb{ a * -b = - (a * b) } $$

2.The product of two numbers of the same sign is positive.: $$ \pmb{ -a * -b = a * b } $$

Here are some very simple examples to illustrate:
$$a. \quad -3 * -3 = 9 $$ $$b. \quad 2 * -3 = -6 $$ $$c. \quad 2 * 2 = 4 $$ $$d. \quad -3 * 6 = -18 $$
$$e. \quad -3 * 3 * -3 \\\quad= -9 * -3 \\\quad= 27 $$
$$f. \quad -2 * 2 * -2 * 2 * -2 \\\quad= -4 * -4 * -2 \\\quad= 16 * -2 = -32 $$

And finally, a mnemonic often used, a friend is '+', an enemy is '-':
+ + ⇒ + | a friend of a friend is my friend
+ − ⇒ − | a friend of an enemy is my enemy
− + ⇒ − | an enemy of a friend is my enemy
− − ⇒ + | an enemy of an enemy is my friend