Dans la leçon précédente, nous avons vu les nombres entiers naturels (0, 1, 2, 3...) et comment effectuer des opérations mathématiques avec eux. Il est maintenant temps d'élargir notre vision des nombres avec les entiers relatifs. Les nombres entiers (ou entiers relatifs) sont comme des nombres naturels, mais ils incluent également des nombres négatifs: {...-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...}. L'ensemble des entiers est noté Z.

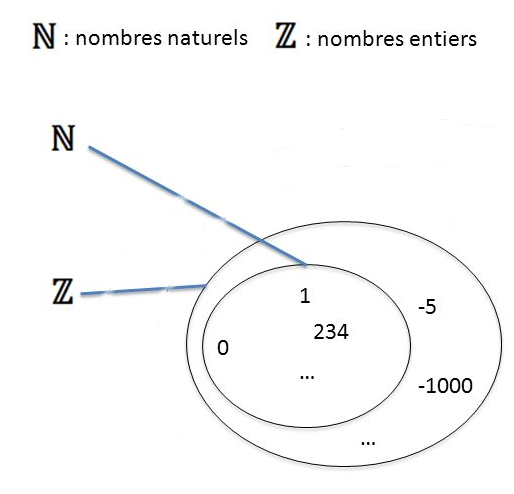
En d'autres termes, l'ensemble des entiers est l'union de l'ensemble des nombres naturels et de leurs opposés. Si a est un nombre naturel, alors -a est un entier de signe opposé. Sur un axe gradué, deux nombres opposés sont symétriques par rapport à l'origine (0).

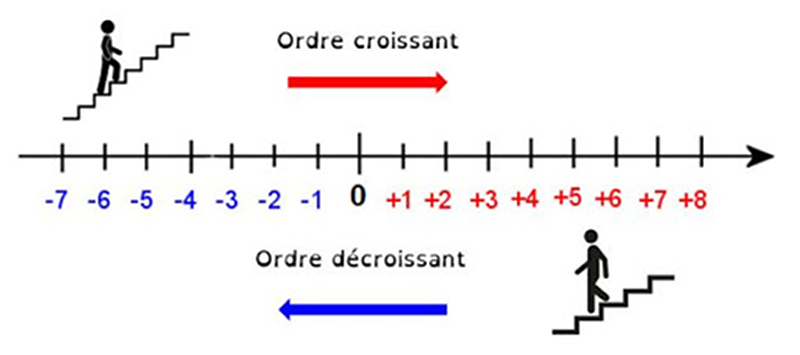
Notons que zéro est considéré comme étant à la fois positif et négatif.

Remarque: certaines personnes peuvent avoir des définitions différentes pour le même mot utilisé pour définir un ensemble de nombres. Certaines personnes disent que zéro n'est PAS un nombre naturel.

Pour être précis, la façon la plus simple est d'utiliser la notation mathématique. Cette notation est stricte et évite donc toute confusion.
Z   : tous les entiers relatifs.
Z^* : (Z étoile) est l'ensemble des entiers relatifs excepté 0 (zéro).
Z⁺ : tous les entiers relatifs positif (équivalent à N).
Z^*₊ : tous les entiers strictement supérieur à 0 (équivalent N⁺).

Au VIIème siècle après JC., le mathématicien indien BRAHMAGUPTA énonça pour la première fois des règles pour opérer sur trois sortes de nombres appelés "biens", "dettes" et "zéro". Les dettes (en quelques sorte les nombres négatifs) étaient alors utilisés en Inde pour le commerce.

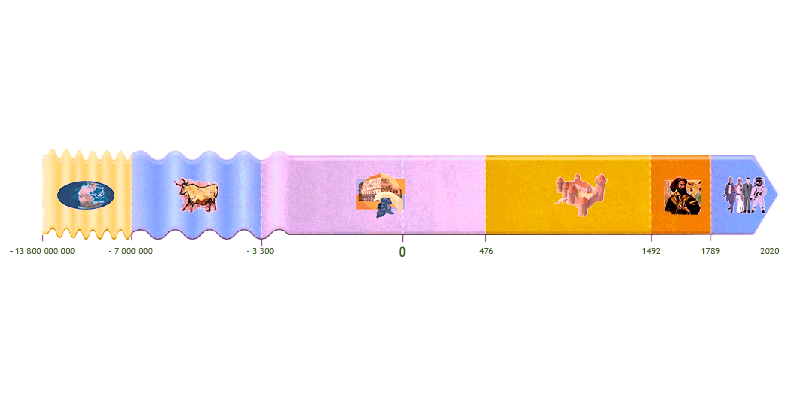
Aujourd’hui nous trouvons des exemples de nombres négatifs absolument partout:
- Ascenseur : pour descendre dans les sous-sols nous avons un signe “-” nous indiquant aller en dessous du rez-de-chaussé.
- Météo : si la température est en dessous de 0°, le signe “-” indiquera cette température négative.
- Jeu vidéo : lorsque l’on perds des points de vie, nous voyons apparaître à l’écran des signe “-” devant les nombres.
- Frise chronologique : une date antérieur à notre année 0 sera notée avec un signe "-" ou sera annotée "avant JC".
- Finance : une banque utilise des nombres positifs pour représenter les dépôts et des nombres négatifs pour représenter les retraits.
- Etc.

Mais si ces nombres négatifs sont aujourd’hui utilisés absolument partout, il faut savoir qu’ils furent très longtemps ignorés, voir méprisés car difficilement appréhendables par l’esprit humain. Voici un petit peu d’histoire qui consolera aussi tous ceux qui rencontrent des difficultés avec les nombres négatifs !

Un peu d'histoire

Bien que le premier ensemble de règles pour traiter les nombres négatifs ait été énoncé au 7ème siècle par le mathématicien indien Brahmagupta, les nombres négatifs étaient encore considérés comme absurdes en Europe au 18ème siècle.

En 1758, le mathématicien britannique Francis Maseres affirmait que les nombres négatifs "... obscurcissent toute la doctrine des équations et obscurcissent les choses qui sont par nature excessivement évidentes et simples".

Les nombres négatifs ne sont pas si faciles.
Que signifient exactement les nombres négatifs?
Comment pouvons-nous prendre 4 stylos si il y en a 3?
Comment pourrions-nous avoir moins que rien?
Pourtant, aujourd'hui, il semble absurde de penser que les nombres négatifs ne sont ni logiques ni utiles.

Qu'est-il arrivé?
Les nombres négatifs ne sont pas quelque chose que nous pouvons facilement appréhender ou imaginer.

Les choses ont prit un tournant lorsque les universitaires européens ont commencé à traduire des textes arabes obtenus d'Afrique du Nord. Les européens ont alors été exposés à de nouvelles façons de penser, et ont commencé à rattraper le retard sur l'Orient et l'Afrique du Nord.

Plutôt que de dire "je dois 30€" et de lire des mots pour voir si je suis dans le positif ou le négatif, je peux écrire "-30€" et savoir que cela signifie que je suis dans le négatif. Les signes positifs et négatifs suivent automatiquement la direction : nous n'avons pas besoin d'une phrase pour décrire l'impact de chaque transaction.

Avec la notation de signe «moins», les mathématiques sont devenues plus faciles et plus élégantes. Peu importait que les négatifs soient «tangibles», ils avaient des propriétés utiles, et nous les avons utilisés jusqu'à ce qu'ils deviennent des objets du quotidien.

Mais ne soyons pas hautains face à la lutte : les chiffres négatifs ont été un énorme changement mental. Même Euler, le génie qui a découvert l'exponentielle et bien plus encore, ne comprenait pas les négatifs comme nous le faisons aujourd'hui. Ils étaient considérés comme des résultats «dénués de sens».

Comme le dirait Bernard de Chartres, Isaac Newton ou encore Blaise Pascal :
Nous sommes "Des nains sur des épaules de géants".

Addition et Soustraction

Bonne nouvelle: ces opérations se font exactement de la même manière que pour les nombre entiers naturels !
Sauf que cette fois-ci, nous pouvons descendre en dessous de 0; notons que ‘-a’ signifie exactement la même chose que ‘0 - a’.

Il y a deux uniques choses à savoir pour nous permettre de devenir très rapidement un véritable ninja dans l’art de réaliser nos opérations:

1. Ajouter un nombre négatif revient à soustraire un positif: $$ \pmb{ (-b) + a = a - b } $$ $$ \pmb{ a + (-b) = a -b } $$

2. Soustraire un négatif revient à ajouter un positif: $$ \pmb{ a - (-b) = a + b } $$

Prenons tout de suite un exemple qui semble compliqué et transformons le en quelque chose de très simple:
$$ 5 + 4 - 3 + (-2) - 2 - (-4) = ? $$

Règle numéro 1 : +(-2) → - 2
Règle numéro 2 : -(-4) → + 4

Nous aurons donc:
$$ 5 + 4 - 3 + (-2) - 2 - (-4) \\= 5 + 4 - 3 - 2 - 2 + 4 \\= 6 $$

Et voila, nous savons déjà tout pour l'addition et la soustraction!

Multiplication et Division

Nous avons encore des bonnes nouvelles!

Comme pour les additions et les soustractions:
- Ces opérations se font de la même manière que pour les nombres entiers naturels.
- Il n’y a que deux choses à savoir.
- La combinaison des signes est la même.

1. Le produit de deux nombres de signe contraire est négatif.: $$ \pmb{ -b * a = - (a * b) } $$ $$ \pmb{ a * -b = - (a * b) } $$

2. Le produit de deux nombres de même signe est positif.: $$ \pmb{ -a * -b = a * b } $$

Voici quelques exemples très simples pour illustrer:
$$a. \quad -3 * -3 = 9 $$ $$b. \quad 2 * -3 = -6 $$ $$c. \quad 2 * 2 = 4 $$ $$d. \quad -3 * 6 = -18 $$
$$e. \quad -3 * 3 * -3 \\\quad= -9 * -3 \\\quad= 27 $$
$$f. \quad -2 * 2 * -2 * 2 * -2 \\\quad= -4 * -4 * -2 \\\quad= 16 * -2 = -32 $$

Et pour finir, un moyen mnémotechnique souvent utilisé, soit '+' un ami et '-' un ennemi:
+ + ⇒ + | un ami d'un ami est mon ami
+ − ⇒ − | un ami d'un ennemi est mon ennemi
− + ⇒ − | l'ennemi d'un ami est mon ennemi
− − ⇒ + | un ennemi d'un ennemi est mon ami