Dans cette introduction nous verrons le vocabulaire et les règles de calculs utilisés pour tous les ensemble de nombres. Cela peut paraître compliqué dans un premier abord, mais pour chaque ensemble (cf. Accès Rapide ci-dessus) nous expliquerons dans le détail et avec des exemples comment procéder. Cette vision générale deviendra ensuite hyper pratique pour consulter rapidement toutes les règles, le vocabulaire et ce que représente chaque ensemble.

Commencons par la big picture, comment sont catégorisés les ensembles de nombres?

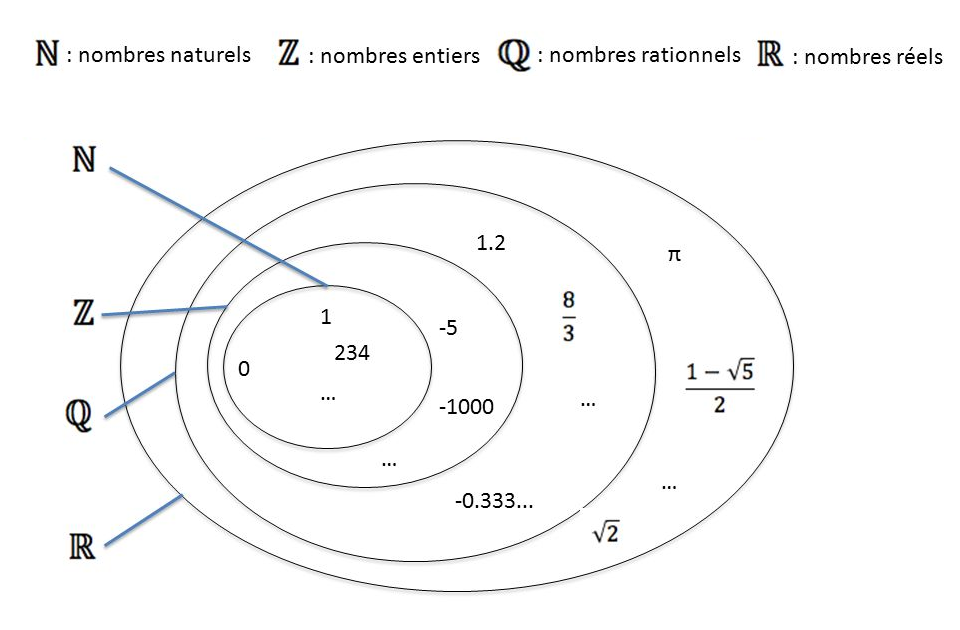
N : Un entier naturel est un nombre positif et "sans virgule" tel que 0, 1, 2, 3...

Z : Un nombre entier (ou entier relatif) est un nombre positif ou négatif et "sans virgule" tel que
  ...-3, -2, -1, 0, 1, 2, 3...

Q : Un nombre rationnel est un nombre qui peut s'écrire sous forme de fraction tel que 1/3, -2/7 etc.

R : Certains nombres comme √2 ou π ne sont pas des rationnels. L'ensemble des réels complète l'ensemble Q.

Tout comme les règles (ci-dessous), les priorités des opérations sont vraies tout le temps. Il faudra les suivre chaque fois que nous aurons un calcul à effectuer :

1. Les calculs entre parenthèses
2. Les puissances
3. La multiplication et la division
4. L’addition et la soustraction
5. En cas d’opérations de mêmes priorités, c'est à notre convenance (on fait comme on veut).

Quelques exemples

Ce vocabulaire et ces règles de calculs vous suivront jusqu'au bout de vos études et resteront inchangés. Cela peut sembler un petit peu lourd au début, mais nous l'utiliserons quotidiennement en math et cela quelque soit le niveau d'étude. C'est parti:

Division

Nous ne divisons jamais par 0 !

Élément neutre

on appelle élément neutre un nombre qui ne modifie pas le résultat d’une opération.

L'addition possède un élément neutre, l'élément nul : a + 0 = a
La multiplication possède un élément neutre, l'unité : a × 1 = a

Nombre inverse

On appelle inverse du nombre a (non nul) le nombre noté a^-1 ou 1/a vérifiant : $$\pmb{a * \frac{1}{a} = 1}$$ ou $$\pmb{a * a^{-1} = 1}$$

Nombre opposé

On appelle opposé du nombre a le nombre noté –a vérifiant : $$\pmb{a + (-a) = 0}$$

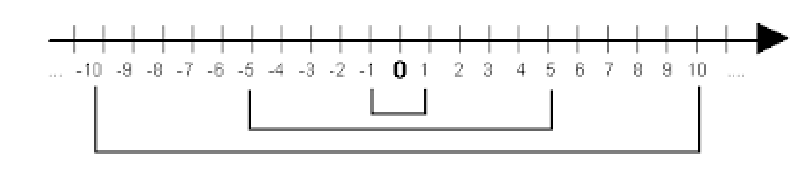
Sur un axe gradué, deux nombres opposés sont symétriques par rapport à l’origine (0).

Opération associative

Une opération est associative si le résultat est invariable quelque soit le regroupement des termes consécutifs. En d'autres termes si l'opérateur (noté ❄︎) possède les propriétés suivantes quels que soient les éléments a, b et c: $$(a ❄︎ b) ❄︎ c = a ❄︎ (b ❄︎ c)$$

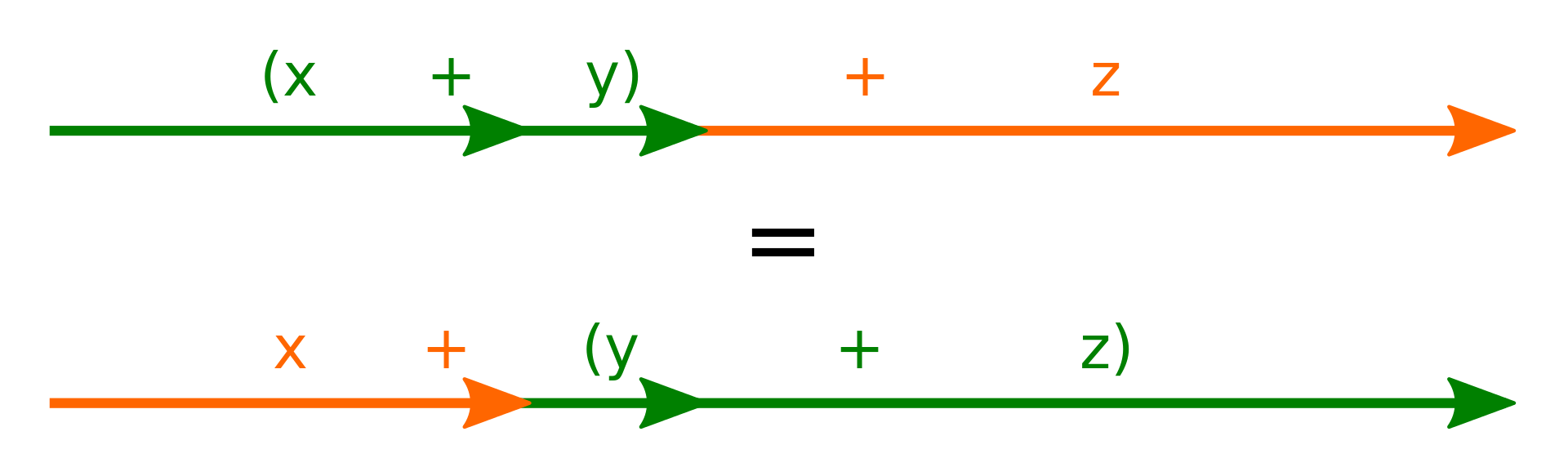
L'addition est associative : (a + b) + c = a + (b + c)
La multiplication est associative : (a × b) × c = a × (b × c)

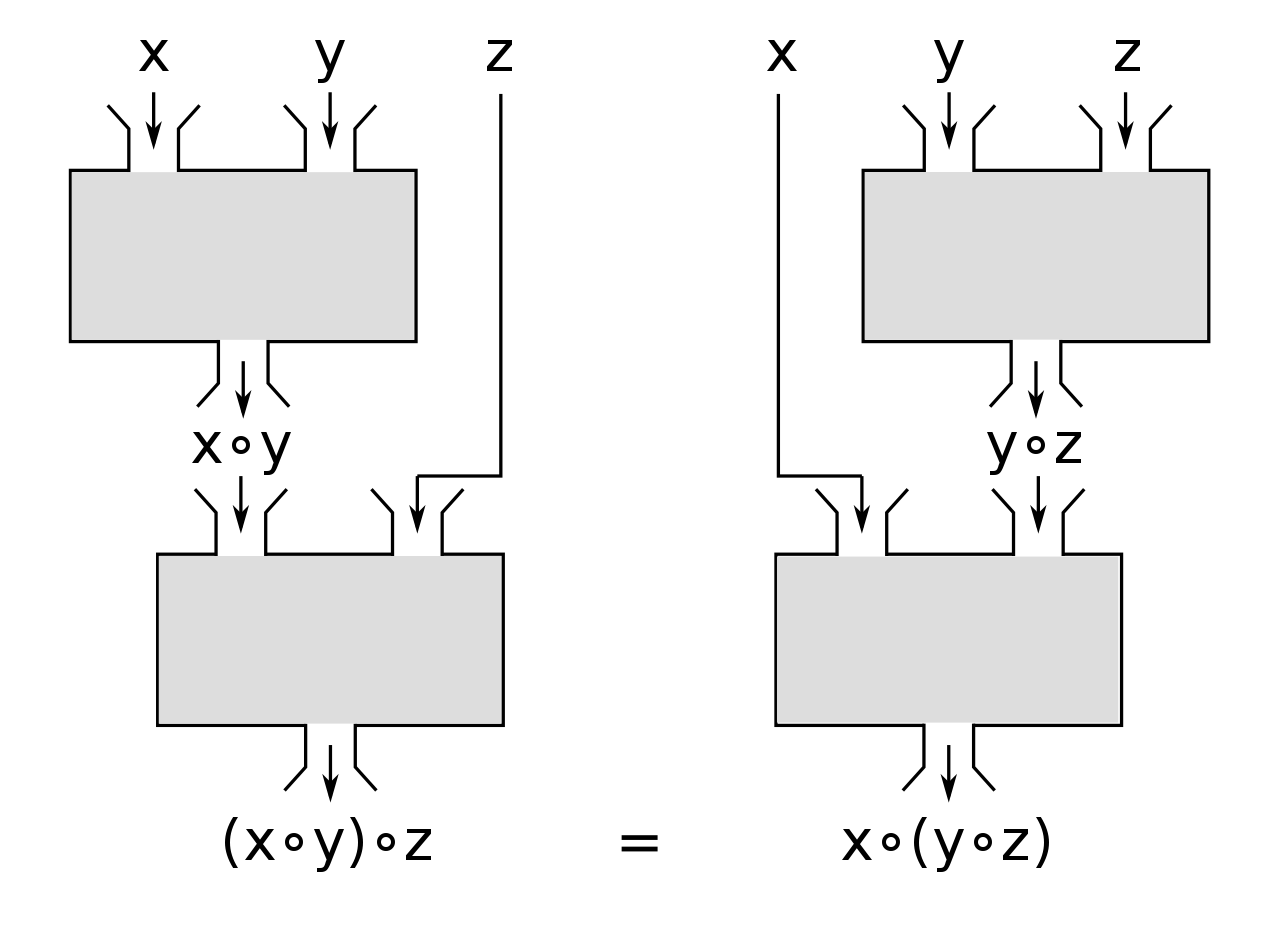
Attention: La soustraction et la division ne pas associatives !

Opération commutative

Une opération commutative est une opération qui permet de changer l’ordre des termes sans en changer le résultat.

L'addition est commutative : a + b = b + a
La multiplication est commutative : a × b = b × a

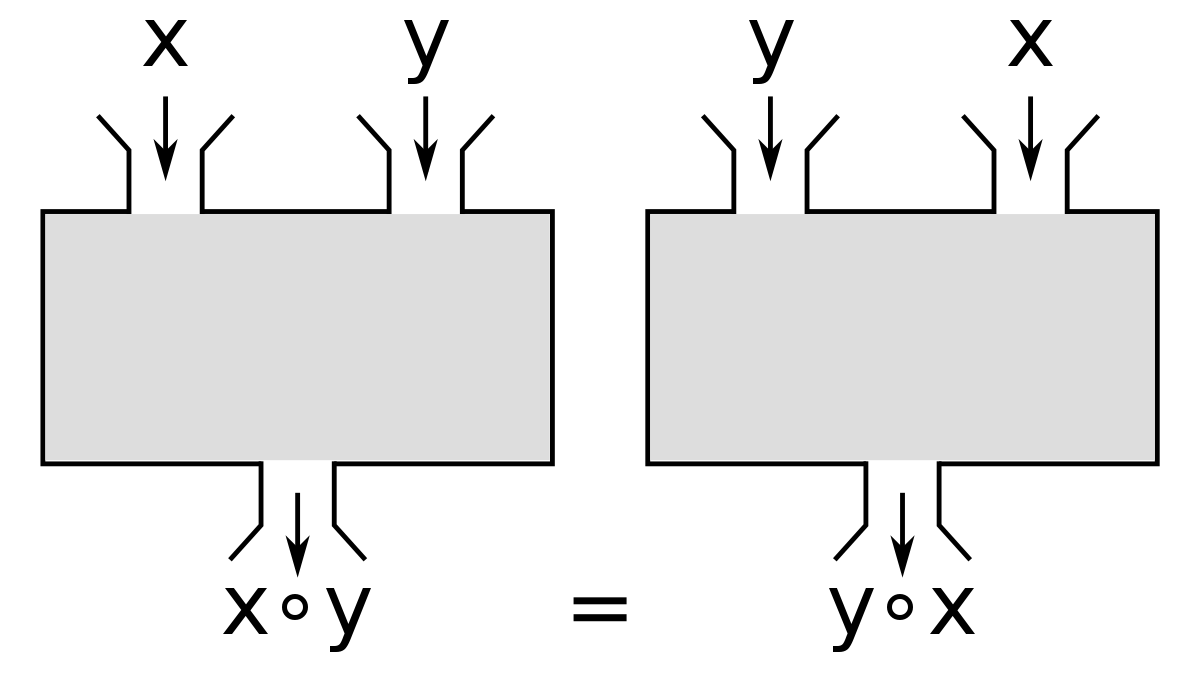
Mathématiquement, cela s'écrirait: $$ \forall x,y\in \mathbb{R} : x+y = y+x$$ $$\forall x,y\in \mathbb{R} : x×y = y×x$$

Attention: La soustraction et la division ne pas commutatives !

Opération distributive

La multiplication est distributive sur l’addition. Cela se traduit comme suit : $$\pmb{a * (b + c) = (a * b) + (a * c)}$$

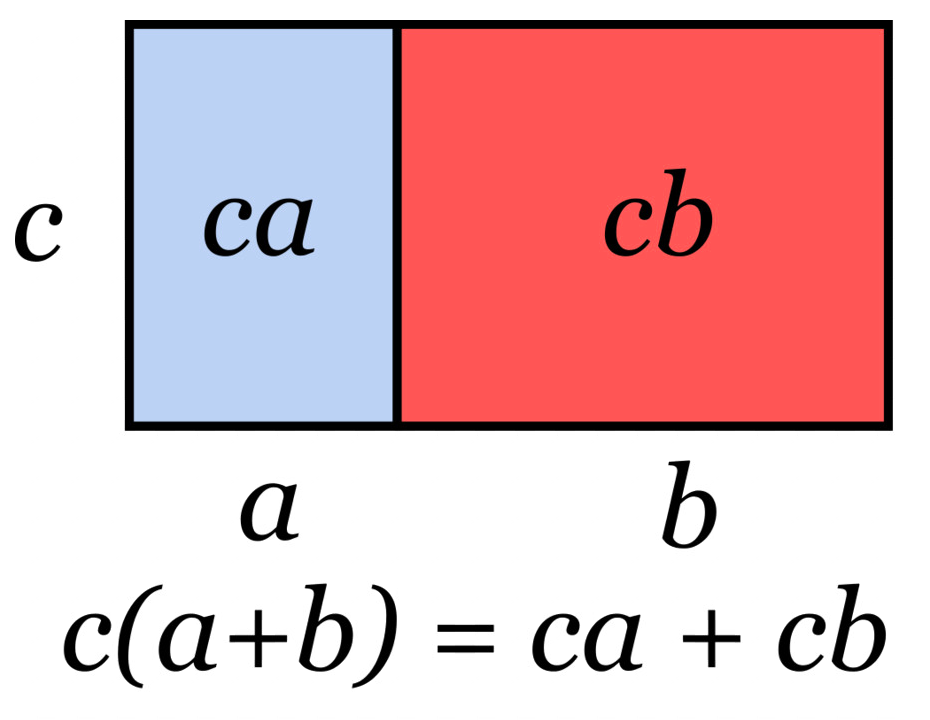
L'image ci-dessus est une démonstration visuelle. Effectivement, nous voyons bien que l'aire du rectangle total "c * (a + b)" est bien égal à la somme des deux aires intérieures "(c * a) + (c * b)".

Opération stable

En mathématiques, on dit qu'une partie A d'un ensemble E est stable (ou close) pour une opération définie sur E si cette opération, appliquée à des éléments de A, produit un élément de A.

Par exemple l'ensemble N (entiers naturels ou entiers positifs) est stable pour l'addition et la multiplication : cela signifie que si j'additionne ou multiplie deux entiers naturels quelconques, le résultat sera encore un entier naturel.

N n'est pas stable pour la soustraction (ou la division) : par exemple 2 - 3 = -1, qui n'est pas dans N.

Voilà ! Nous connaissons désormais les règles du jeu pour effectuer des calculs mathématiques. Nous allons pouvoir rentrer dans les détails pratiques pour chaque ensemble de nombres (cf. Accès Rapide).