Dans nos cours précédents, nous avons vu comment effectuer les quatre opérations fondamentales (additionner, soustraire, multiplier et diviser) sur les nombres naturels ainsi que les entiers relatifs. Cependant, nous n’avions pas traité les cas particulier pour la division, par exemple lorsque cela ne divisait pas exactement les choses. C'est le sujet de ce cours important: la division euclidienne - ou division avec reste.

Ne nous inquiétons pas, le nom et l'importance de ce cours cachent quelque chose de très facile à comprendre et à réaliser ;)

La division euclidienne et les algorithmes pour la calculer sont fondamentaux pour de nombreuses questions telles que la recherche du plus grand diviseur commun (PGCD) ou en arithmétique modulaire - opération modulo (utilisé absolument partout en informatique: du site web à la cryptographie en passant par les jeux vidéo).

Mais d'abord, un petit rappel sur la division!

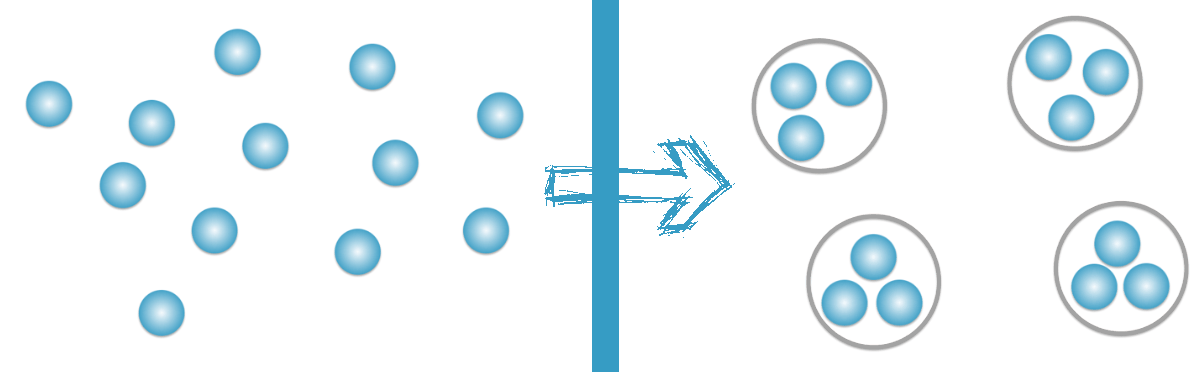
La division nous permet de calculer les problèmes de partage, c'est l'opposé de la multiplication.

Exemple:
Il y a 12 bonbons bleus et 4 amis veulent les partager, comment divisons-nous les bonbons?

La réponse peut sembler évidente: si chaque ami prend 3 bonbons, nous sommes tous bons :) La division est le fait de diviser en parties (ou groupes) égales. C'est le résultat d'un "partage équitable".

Note:
Comme nous l'avons dit, une autre façon de penser à la division est de faire l'opposé de la multiplication. En prenant l'exemple précédent, nous avons:

--> 12 / 4 = 3 (nous donnons 3 bonbons à chacun de nous)

Maintenant, si nous inversons l'opération en utilisant le résultat, nous remplaçons le ‘=’ avec le signe ‘x’ (multiplier) et la division ‘/’ avec le signe ‘=’:

--> 12 = 3 x 4 (si 3 bonbons sont donnés à chacun de nous, nous avons partagé un total de 12 bonbons)

Telle est, en effet, la définition mathématique de la division: $$ \pmb{a / b = a * \frac{1}{b}} $$

La multiplication est un excellent moyen de vérifier notre division et de maîtriser nos opérations. Mais souvenez-vous de cette règle, c'est la seule à savoir quand il s'agit de division:
Nous ne divisons jamais par 0!

Mais... Parfois ça ne se partage pas parfaitement!

Occupons nous en!

Comme nous l'avons vu, la division divise en un nombre égal de parts, mais... il peut y avoir quelque chose qui reste. Revenons à notre exemple précédent, mais cette fois, les 4 amis ont 13 bonbons bleus à partager (un de plus qu'auparavant):

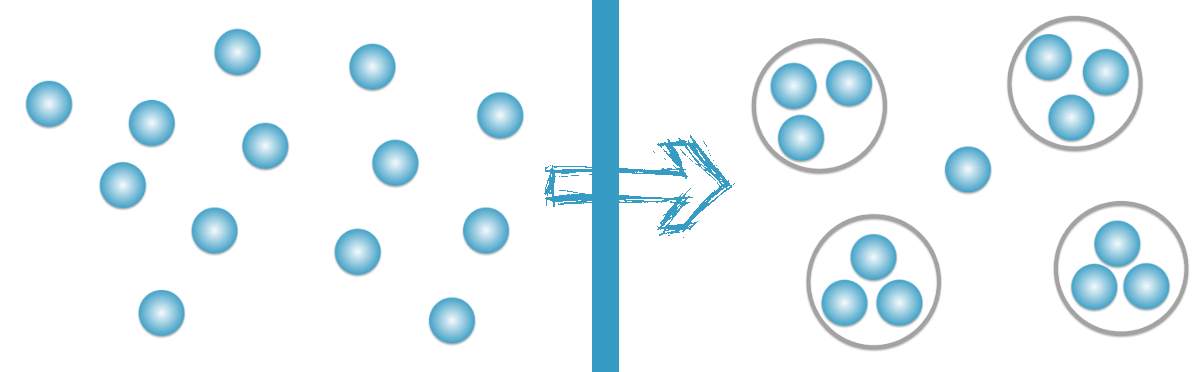
Nous pouvons voir qu'il en reste 1; nous appelons cela le Reste.
Remarque: il pourrait éventuellement être possible de couper ce bonbon restant en quatre (un quart - 1/4 - de bonbon pour chacun), mais cela est abordé dans le cours traitant de Fractions.

Nous allons maintenant apprendre à effectuer toutes les divisions (même avec de grands nombres) à la main. Mais d'abord, un bref aperçu du vocabulaire.

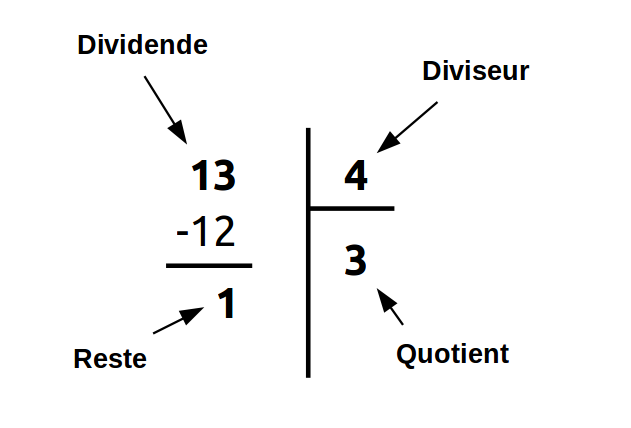
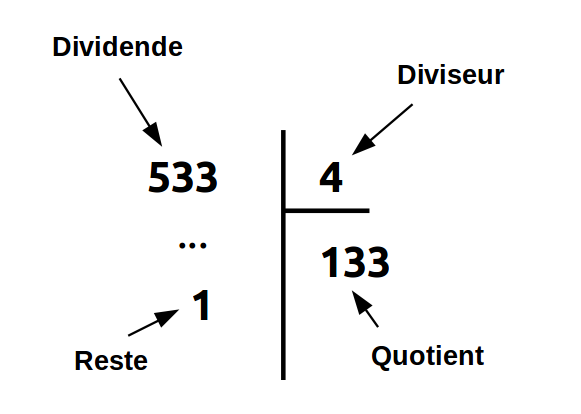
Dividende, diviseur, quotient et reste

Chaque partie d'une division a un nom:

  - Dividende: Le dividende est le nombre que nous divisons.
  - Diviseur: Le diviseur est le nombre par lequel nous divisons.
  - Quotient: Le quotient est le résultat principal (le nombre de bonbons entiers que nous donnons à chacun).
  - Reste: Le reste.

Par exemple: 13 (dividende) ÷ 4 (diviseur) = 3 (quotient) 'R'1 (reste)

Super, je pense que nous sommes maintenant pleinement prêts à aborder le processus!

Pour effectuer une division à la main, chaque étudiant apprend (sans le savoir) un algorithme qui est l'un des plus anciens algorithmes utilisés (il est apparu avec Euclide vers 300 avant J.-C).

Nous décomposerons le processus étape par étape (seulement 2 étapes à répéter) à travers un exemple: 533 ÷ 4.

Voici la légende des couleurs utilisée:

Rouge: le nombre que nous essaierons de diviser par notre diviseur.
Bleu: le diviseur, combien en avons-nous dans le nombre rouge?
Vert: le nombre de diviseurs trouvé dans le nombre rouge.
Jaune: soustraire «bleu x vert» du nombre rouge.

Départ

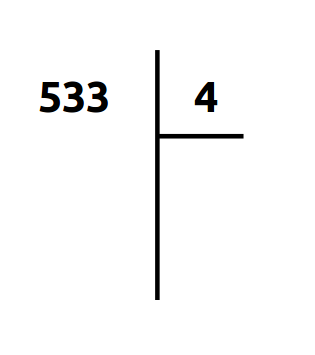
Nous commençons le processus en utilisant le chiffre le plus à gauche du dividende.

A. Combien de fois en avons-nous 4 (bleu) dans 5 (rouge)?

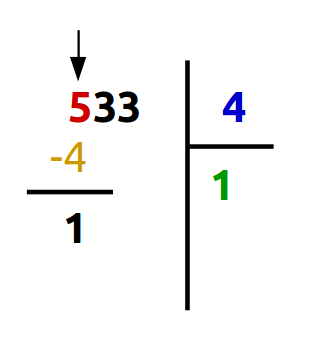
Sur cinq, on ne peut compter jusqu'à quatre qu'une seule fois (vert).

Nous mettons ce nombre dans la case quotient (vert) et effectuons la soustraction (jaune):
5 - (4 x 1) = 1

B. Descendre les prochains chiffres du dividende.

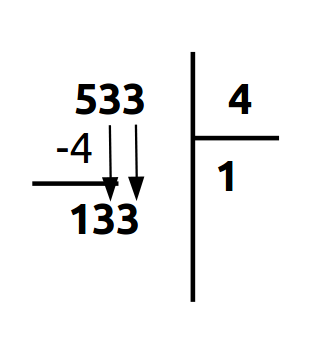
Tout ce que nous avons à faire maintenant est de descendre les prochains chiffres du dividende au niveau du résultat et de répéter l'étape A.

Nous répétons le processus avec le résultat de la soustraction comme dividende.

A. Combien de fois avons-nous 4 (bleu) dans 1 (rouge)?

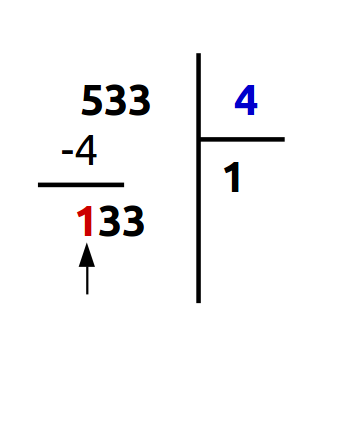
Ici, 1 est inférieur à 4. Dans ce cas, il suffit de répéter cette étape en incluant le chiffre suivant du dividende (cf. suivant).

A.bis Inclure le chiffre suivant du dividende

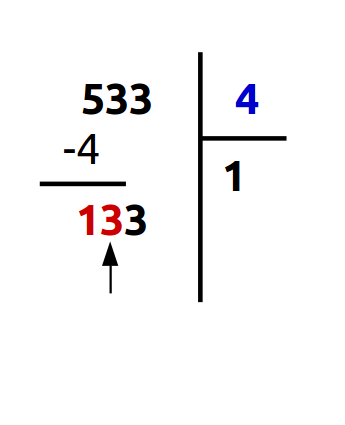
Comme nous l'avons dit, nous incluons le chiffre suivant du nouveau dividende (rouge) pour effectuer cette étape.

A. Combien de fois avons-nous 4 (bleu) dans 13 (rouge)?

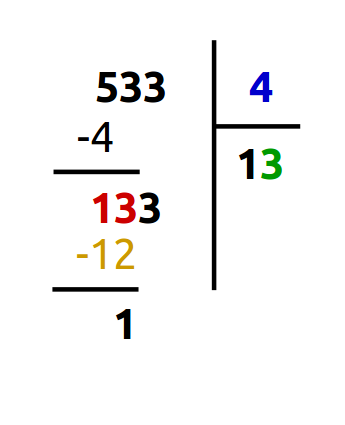
Dans treize, on peut compter jusqu'à quatre seulement 3 fois (vert).

Nous mettons ce nombre dans la case quotient (vert) et effectuons la soustraction (jaune):
13 - (4 x 3) = 1

Et enfin...

B. Descendre le prochains chiffres du dividende.

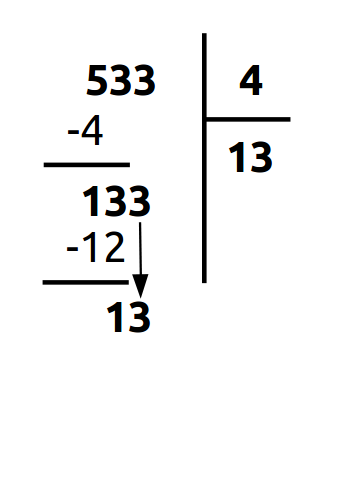
Comme précédemment (étape B), nous descendons les chiffres suivants du nouveau dividende et répétons à partir de A.

A. Finito!

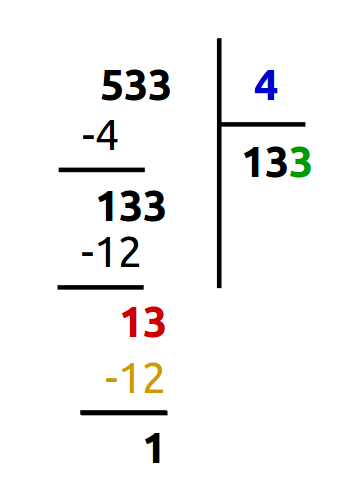
Ici, nous effectuons les mêmes opérations qu'avant...

Une fois que le nouveau dividende est inférieur au diviseur, notre processus est terminé!

Nous avons trouver: 533 ÷ 4 = 133, 'R'1
Nous pouvons aussi dire que: 533 = 4 x 133 + 1

Woaw, super pratique!

Pour toujours trouver le PGCD, nous utiliserons l'algorithme d'Euclide:

- Effectuer la division euclidienne du plus grand nombre (noté a) de la fraction sur le plus petit nombre (noté b) et garder le reste (noté r).

- Tant que le reste est différent de 0, nous réitérons la division en remplacant a par b et b par r.

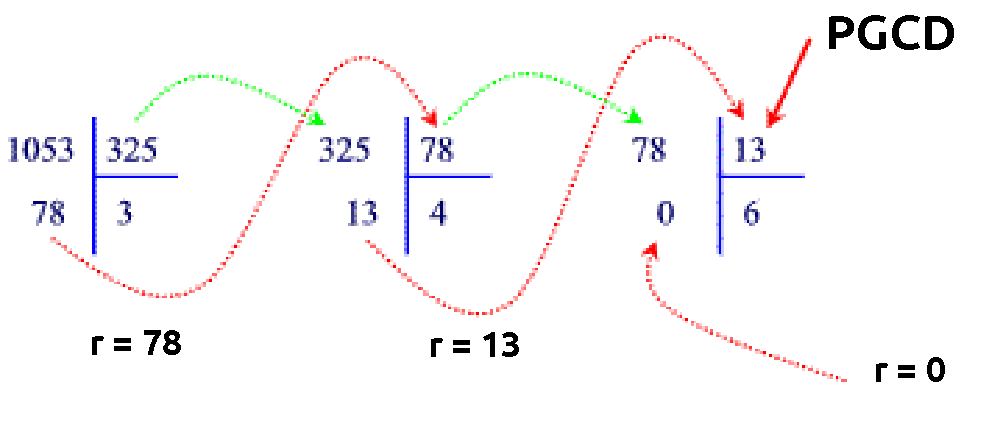
On pourra ainsi écrire : $$1053 = 81 \color{green}{\textbf{ * 13}}$$ $$325 = 25 \color{green}{\textbf{ * 13}}$$

Nous utiliserons beaucoup le PGCD, en commençant par la maîtrise des fractions : que ce soit pour les simplifier ou pour effectuer des opérations.