Un entier naturel est un nombre positif et "sans virgule" tel que 1, 2, 3... et 0. Le plus petit élément est 0 et il n'y a pas de plus grand élément : on peut compter sans jamais s'arrêter.

Les entiers naturels sont les nombres les plus utilisés dans la vie courante, ils permettent de dénombrer un nombre distinct d'objets (ou d’unités). Par exemple, nous pouvons avoir 2 stylos, 1 chat et un billet de 5 euros dans notre poche etc.

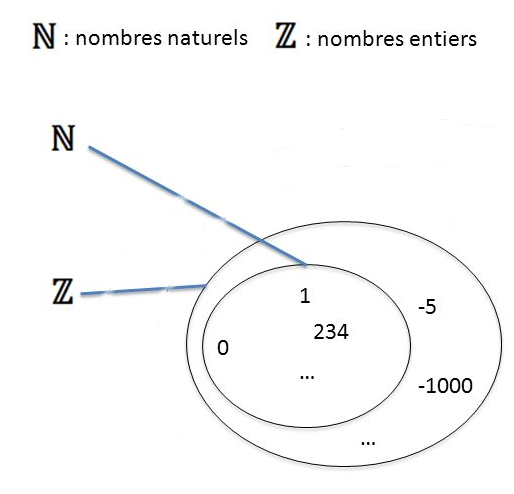
L'ensemble des nombres entiers naturels est noté N, c’est une infime partie (même si elle est infinie) des nombres existants. C’est par exemple un ensemble plus petit que celui des entiers (relatifs) Z.

La théorie s'arrête là ! Nous allons maintenant nous lancer dans le vif du sujet. Nous verrons d’abord comment écrire les nombres entiers, puis ce que signifie les opérations mathématiques et comment les effectuer.

Que représente le nombre 281 ?

Ce nombre veut dire que nous avons 2 centaines, 8 dizaines et 1 unité. Cela s'écrit aussi: $$ \pmb{\color{darkred}{2}\color{goldenrod}{8}\color{darkgreen}{1} = \color{darkred}{200} + \color{goldenrod}{80} + \color{darkgreen}{1}}$$

Pour faciliter la visualisation, nous pouvons mettre ce nombre dans un tableau appelé tableau de numération comme ci-dessous:

Dans un nombre entier, le chiffre le plus à droite est le chiffre des unités, qu'on écrit dans la colonne des unités. Celui immédiatement à sa gauche est le chiffre des dizaines, qu'on écrit dans la colonne des dizaines. On complète le tableau ainsi de suite de la droite vers la gauche, jusqu'à ce que tous les chiffres soient écrits.

Remarque : Plus un chiffre est situé vers la gauche du nombre, plus sa valeur est grande. Par exemple, 6 centaines c'est plus grand que 6 dizaines car les centaines sont plus à gauche que les dizaines.

Addition

Faire une addition c’est ajouter des quantités, nous disons alors que nous calculons la somme de plusieurs termes (ou nombres). Par exemple si nous comptons les pas que nous faisons en avant : si nous avançons d’un pas puis de deux pas, nous aurons avancé de 1 + 2 = 3 pas au total. Ci-dessous le tableau des additions des chiffres de 1 à 10 :

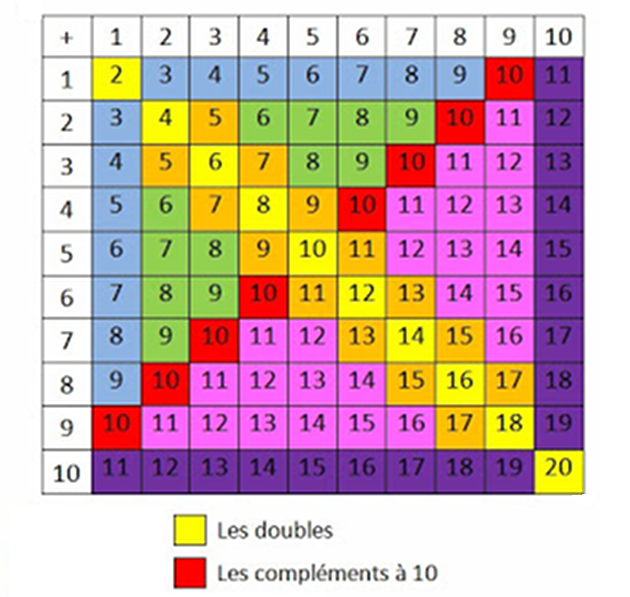
La bonne nouvelle, c'est que nous n'avons pas besoin de retenir ce genre de tableaux et que nous allons pouvoir utiliser notre tableau de numérotation vierge pour effectuer des additions (même beaucoup plus complexes). Nous disposons les nombres l’un au-dessous de l’autre en alignant en colonne les chiffres (unités de numération), puis nous ajoutons les chiffres, colonne par colonne, à partir de la droite.

Attention: nous ne devons pas oublier de reporter la retenue lorsque la somme des chiffres est supérieure à 10 (comme le montre notre exemple de droite).

Dans le calcul d'une somme, l'ordre des termes n'a pas d'importance (l’opération est dite commutative): $$ 2 + 4 = 4 + 2 = 6 $$

Dans le calcul d'une somme, nous pouvons regrouper des termes pour faciliter le calcul (l’opération est dite associative): $$ 8 + 2 + 8 + 2 = (8 + 2) + (8 + 2) = 20 $$

Soustraction

La soustraction est une opération qui permet de calculer la différence entre deux nombres (ou plus). Cette différence entre 2 nombres est le nombre qu'il faut ajouter à l'un pour obtenir l'autre.
Disons que j’ai 1 stylo dans ma trousse, combien m’en faut-il de plus pour en avoir 3 ?

La réponse sera : 3 - 1 = 2.
Il me manque donc 2 stylos pour en avoir 3.

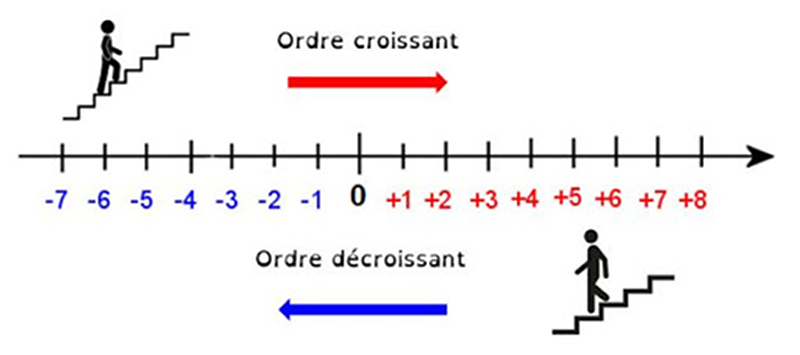
Une autre manière de voir la soustraction est le fait d’enlever des quantités. Par exemple en montant et descendant des escaliers : si nous montons 3 marches puis en descendons 1, nous aurons monté 3 - 1 = 2, soit 2 marches au total.

Pour soustraire deux nombres on dispose les termes de la même manière que pour une addition, puis on soustrait les chiffres, colonne par colonne, à partir de la droite. Si le nombre du dessus est inférieur à celui du dessous, on ajoute 10 au chiffre du haut, puis nous reportons la retenue (-1) sur la colonne de gauche.

Dans le premier exemple, nous voyons dans la colonne des dizaines que 4 est inférieur à 5. Nous aurons donc (4 + 10) - 5 = 14 - 5 = 9. Puis nous reportons la retenue -1 sur la colonne de gauche.

Vérification

Si nous avons un petit doute, le calcul de la vérification permet de vérifier rapidement le résultat. Il suffit pour cela de vérifier quel notre résultat + le terme soustrait = le premier nombre. Avec les deux opérations réalisées ci-dessus, nous aurons donc:

Parfait, nous retombons bien sur nos nombres initiaux : les calculs sont vérifiés !

Soustraire un nombre plus grand?

Dans l’ensemble des nombres entiers naturels, cette opération est impossible!
On dit que l’opération n’est pas stable dans cet ensemble.
Mais pas de panique car le prochain cours, celui des nombres entiers relatifs, nous explique comment surmonter ce problème ;)

Multiplication

La multiplication est une opération qui permet de calculer le produit entre deux nombres. La multiplication correspond à une addition répétée plusieurs fois. Elle permet de grandement simplifier les écrits ainsi que les calculs.

Prenons par exemple "3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3" (il y en a 11), ce calcul peut être beaucoup plus simplement écrit 11 * 3. Nous dirons aussi que nous avons 11 fois le nombre 3, soit un total de 33. Ci-dessous le tableau des multiplications des chiffres de 1 à 10 :

Lorsque l’on multiplie par 10, on décale tout simplement chaque chiffre dans la case de gauche. Par exemple 20 x 10 = 200 (le 2 des dizaines est devenu le 2 des centaines).

Nous avons maintenant l’habitude (c’est toujours la même technique), nous commençons par disposer les nombres l’un au-dessous de l’autre en alignant en colonne les chiffres (unités de numération), puis nous multiplions les chiffres, colonne par colonne, à partir de la droite.

Attention !!!
Lorsque le multiplicateur est un nombre composé de plusieurs chiffres, on effectue les calculs chiffre après chiffre avec l'ensemble des chiffres du nombre du haut.
Puis, pour le chiffre suivant du multiplicateur (du bas):
On va à la ligne et on décale les résultats d'une colonne (voir l'exemple de droite).

Attention: nous ne devons pas oublier de reporter la retenue lorsque le produit des chiffres est supérieure à 10 (cette retenue est à additionner).

Dans le calcul d'un produit, l'ordre des termes n'a pas d'importance (l’opération est dite commutative): 2 * 4 = 4 * 2 = 8

Dans le calcul d'un produit, nous pouvons regrouper des termes pour faciliter le calcul (l’opération est dite associative): 3 * 2 * 3 * 2 = (3 * 3) * (2 * 2) = 36

Félicitations, nous venons d'obtenir les bases les plus fondamentales en mathématiques !!
Que les maths soient avec nous pour la suite !

Division

Maintenant que nous avons appris à multiplier les entiers, la division devrait être un jeu d'enfant car ces opérations suivent les mêmes règles. La division nous permet de calculer les problèmes de partage, c'est l'opposé de la multiplication.

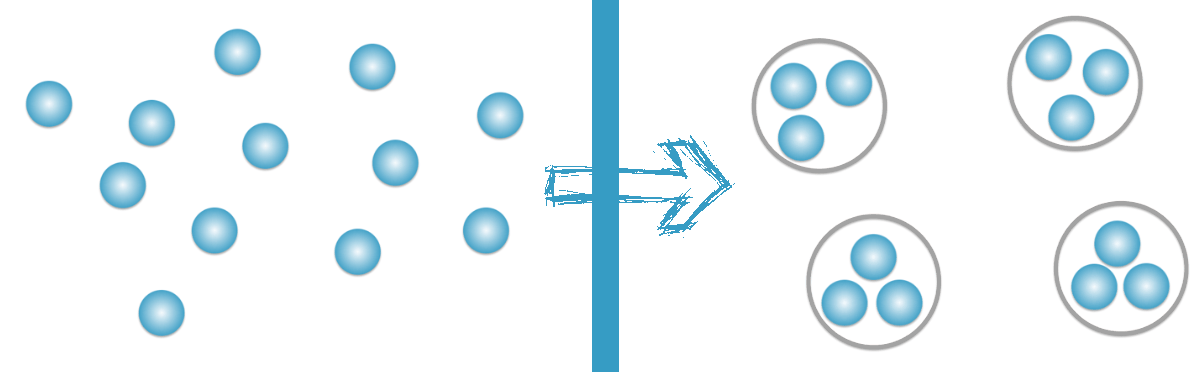
Exemple:
Il y a 12 bonbons bleus et 4 amis veulent les partager, comment divisons-nous les bonbons?

La réponse peut sembler évidente: si chaque ami prend 3 bonbons, nous sommes tous bons :) La division est le fait de diviser en parties (ou groupes) égales. C'est le résultat d'un "partage équitable".

Note:
Comme nous l'avons dit, une autre façon de penser à la division est de faire l'opposé de la multiplication. En prenant l'exemple précédent, nous avons:

--> 12 / 4 = 3 (nous donnons 3 bonbons à chacun de nous)

Maintenant, si nous inversons l'opération en utilisant le résultat, nous remplaçons le ‘=’ avec le signe ‘x’ (multiplier) et la division ‘/’ avec le signe ‘=’:

--> 12 = 3 x 4 (si 3 bonbons sont donnés à chacun de nous, nous avons partagé un total de 12 bonbons)

Telle est, en effet, la définition mathématique de la division: $$ \pmb{a / b = a * \frac{1}{b}} $$

La multiplication est un excellent moyen de vérifier notre division et de maîtriser nos opérations. Mais souvenez-vous de cette règle, c'est la seule à savoir quand il s'agit de division:
Nous ne divisons jamais par 0!

Mais... Parfois ça ne se partage pas parfaitement!

En effet, parfois, nous avons un reste; nous aborderons ce cas et d'autres plus complexes dans un cours dédié: «La division euclidienne» ;)