Labyrinthe crée par un algorithme de Kruskal (taille de 75x50).

Inondation (Flooding) depuis le coin supérieur gauche.

L'arbre de décision présentant la topologie de la structure de données.

Le générateur de labyrinthe de Kruskal est une version aléatoire de l'algorithme de Kruskal : une méthode pour produire un Minimal Spanning Tree (Arbre couvrant de poids minimal* - *traduction litéral) à partir d'un graphe pondéré.

Kruskal est intéressant car il ne "pousse" pas comme un arbre : il sculpte au hasard des passages dans tout le labyrinthe, cela le rend très amusant à regarder. Malgré tout, il en résulte un labyrinthe parfait à la fin.

La contrepartie est d’exiger un espace de stockage proportionnel à la taille du labyrinthe. L'algorithme utilise dans un ordre aléatoire chaque passage possible entre les cellules.

Une fois que nous avons tous les passages possibles dans un grand "sac" et un identifiant unique associé à chaque cellule, tout ce dont nous avons besoin de faire est de choisir un des passages au hasard, vérifier si les cellules voisines appartiennent à un identifiant (sous-ensemble) différent et les unifier dans le cas échéant.

Etapes

L'algorithme aléatoire modifie simplement la première étape de la boucle de sorte qu'au lieu de tirer le passage avec le poids le plus faible, est tiré un passage au hasard.

Code

Maze KruskalS(int width, int height)
{
  Maze maze(width, height);

  // Create a set with all connecting edges
  // Create a vector of buckets for each cell with their id.
  Set edges(maze);                  // #edges = (height - 1) * width + (width - 1) * height
  BucketsVector bucketCells(maze);  // #buckets = #cells = height * width

  // While the set of edges is not empty
  while (!edges.empty())
  {
    // Randomly get an edge and remove it from the set
    auto edge = GetRandom(edges);

    // If cells are not already in the same bucket: Connect them and Merge Buckets
    if (BucketId(edge.first) != BucketId(edge.second))
    {
      Connect(edge.first, edge.second);
      MergeBuckets(bucketCells, edge);
    }
  }

  return maze;
} 

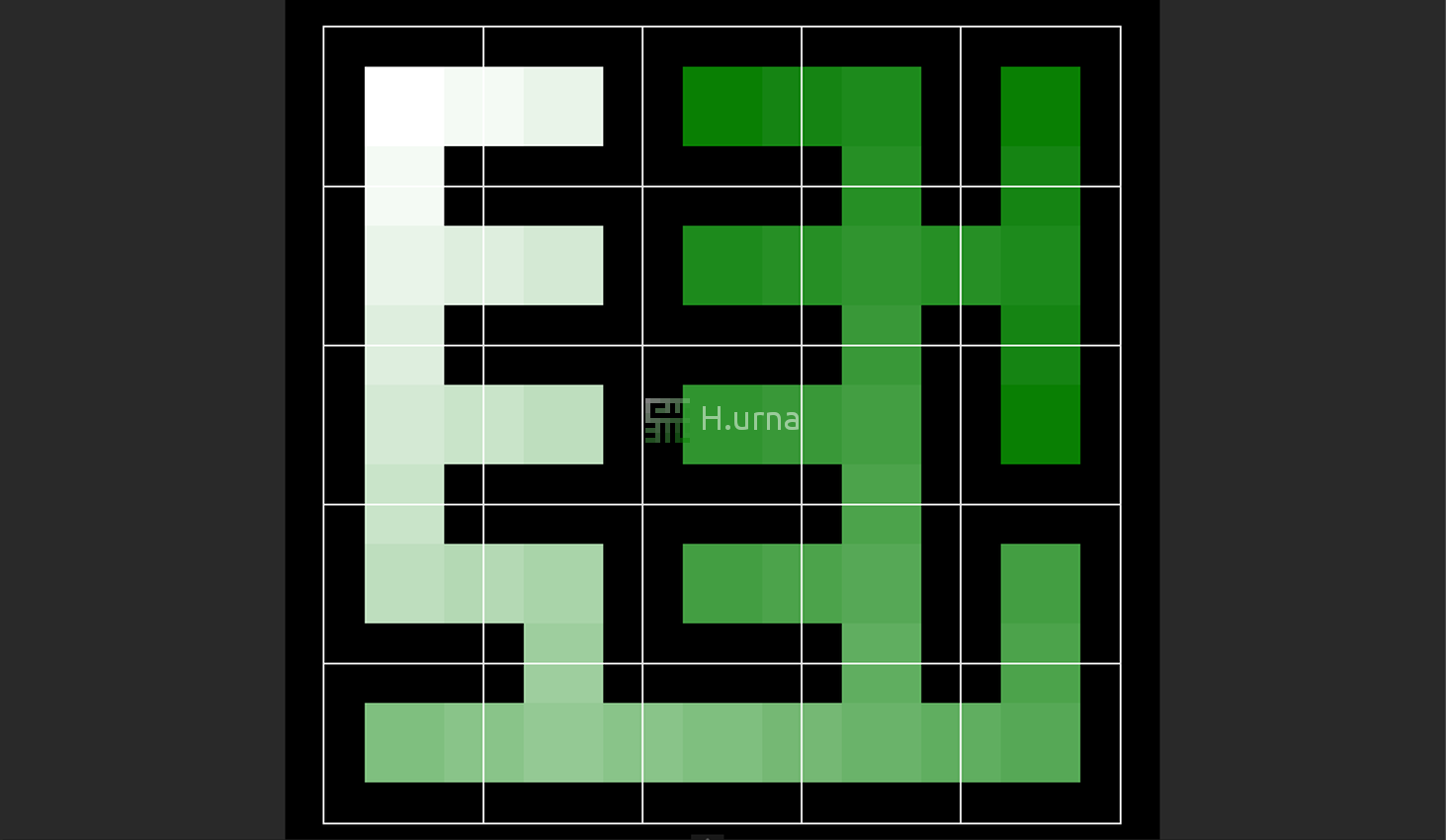
Les labyrinthes générés ont tendance à avoir de nombreux cul-de-sac très courts, donnant au labyrinthe un aspect "hérissé". Cet algorithme donne des labyrinthes avec un facteur de "rivière" bas, il reste cependant plus grand que celui des labyrinthes issues de l'algorithme de Prim.

1. Selection d'un passage au hasard.

2. Les deux cellules sont dans leur propre compartiment (non connectées par un chemin quelconque):
Connecter et fusionner leur ensemble (identifiants).

3. Après quelques itérations...

4. Quelques nouvelles itérations plus tard : le passage sélectionné concerne deux cellules déjà connectées au même chemin (même identifiant).
Le passage est simplement ignoré (cf. slide suivante).

5. Un nouveau popssible lien est sélectionner.

6. Après quelques nouvelles itérations...

7. Tous les liens possibles (passages) sont traités ( les identifiants sont fusionnés en un unique) : le labyrinthe est terminé !

Sautez à bord de l' H.urna Explorer pour créer et voir vos labyrinthes avec Kruskal.