Accès Rapide
Applications
- Utilisé en sous-routine par l'algorithme de statistique d'ordre de rang k (QuickSelect).
- Utilisé en sous-routine par l'algorithme de Tri rapide (Quick Sort).
Construction
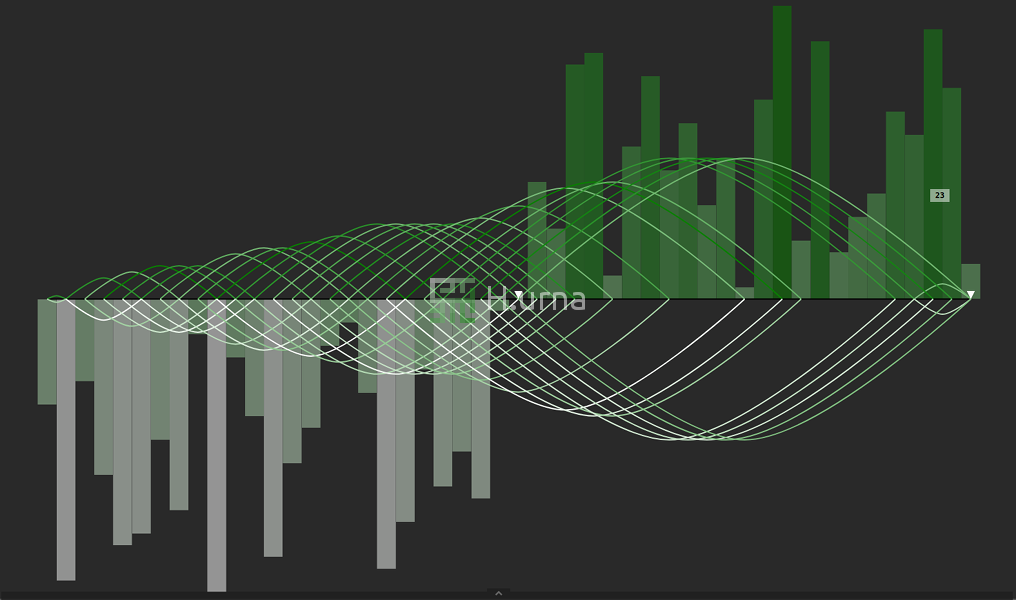
L'algorithme de Partitionnement réordonne la séquence de sorte que tous les éléments avec des valeurs inférieures au pivot (argument de la fonction) se positionneront à gauche de celui-ci et tous ceux avec des valeurs supérieures à droite (les valeurs égales peuvent se trouvées d'un côté comme de l'autre).
Etapes
- 1. Placez le pivot à la fin de la séquence pour plus de commodité.
- 2. Créer un pointeur sur le début de la séquence.
- 3. Pour chaque élément, si sa valeur <= pivot:
- Échanger l'élément avec celui sous le pointeur.
- Incrémenté la position du pointer.
- 4. Remettre le pivot à la position finale du pointeur.
Code
Iterator Partition (Iterator begin, Iterator pivot, Iterator end)
{
if (distance(begin, end) < 2 || pivot == end)
return pivot;
auto pivotValue = *pivot; // Keep the pivot value;
swap(*pivot, *(end - 1)); // Put the pivot at the end for convenience
auto store = begin; // Put the store pointer at the beginning
// Swap each smaller before the pivot item
for (auto it = begin; it != end - 1; ++it)
{
if (Compare(*it, pivotValue))
{
swap(*store, *it);
++store; // Increment store position
}
}
// Replace the pivot at its good position
swap(*(end - 1), *store);
return store;
}
}
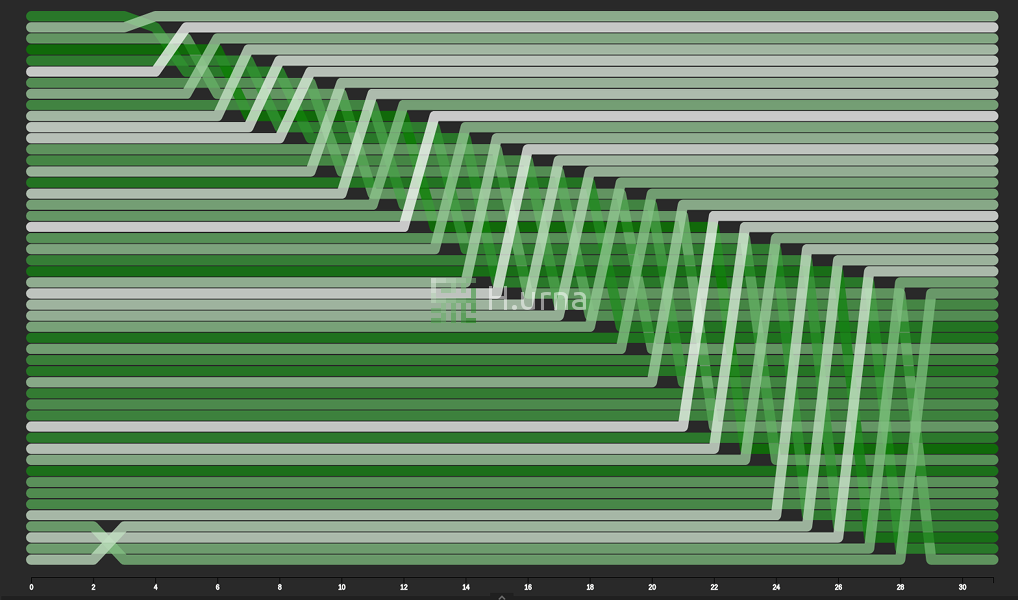
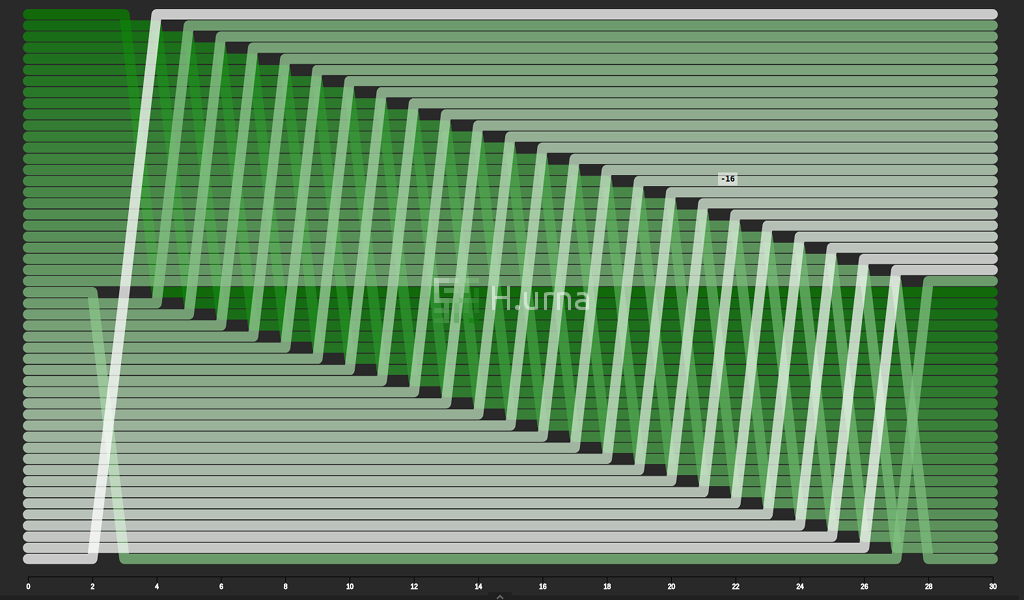
Visualisation
Complexité
Temps
Le partitionnement ne doit passer par tous les éléments qu'une seule fois, il a donc une complexité en O(n) dans tous les cas.
Mémoire
Il n'utilise pas de stockage ni ne fait de récursivité. Il requière donc O(1) d'utilisation mémoire dans tous les cas.


 Jouer en ligne
Jouer en ligne
 Code Source C++
Code Source C++


