Accès Rapide
Dépendances
- Utilise le Partitionnement en sous-routine
Construction
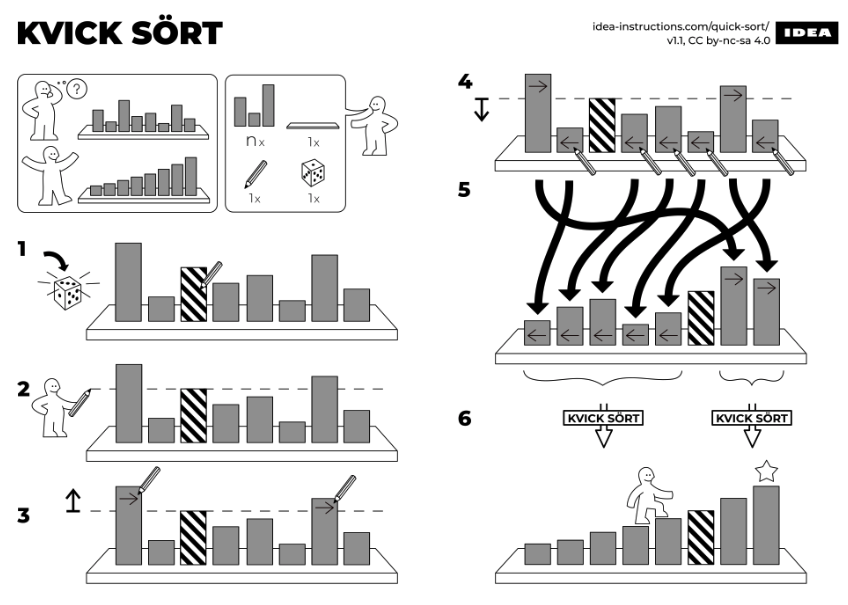
Le tri Rapide (parfois appelé tri par échange de partition) est un algorithme de tri efficace basé sur une approche diviser pour régner. L'algorithme divise d’abord la séquence en deux plus petites : les éléments inférieurs à un pivot dans l'une et ceux supérieurs dans l'autre. Il répète ensuite ce processus récursivement dans chacune de ces nouvelles séquences.
Etapes
- 1. Choisir un élément, appelé pivot.
- 2. Partitionnement : diviser la séquence en deux partitions telles que:
- Tous les éléments inférieurs au pivot doivent être dans la première partition.
- Tous les éléments supérieurs au pivot doivent être dans la seconde partition.
- 3. Effectuer une récursion sur chacune des partitions.
Code
void QuickSort (Iterator begin, Iterator end)
{
const auto size = distance(begin, end);
if (size < 2)
return;
// Pick Pivot € [begin, end] e.g { begin + (rand() % size); }
// Proceed partition
auto pivot = PickPivot(begin, end);
auto newPivot = Partition(begin, pivot, end);
QuickSort(begin, newPivot); // Recurse on first partition
QuickSort(newPivot + 1, end); // Recurse on second partition
}
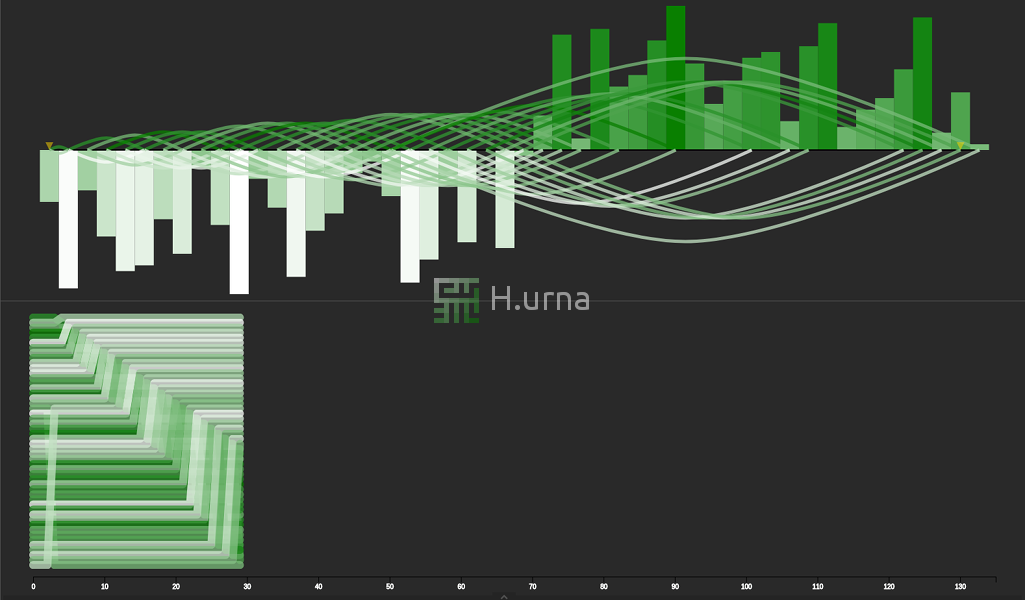
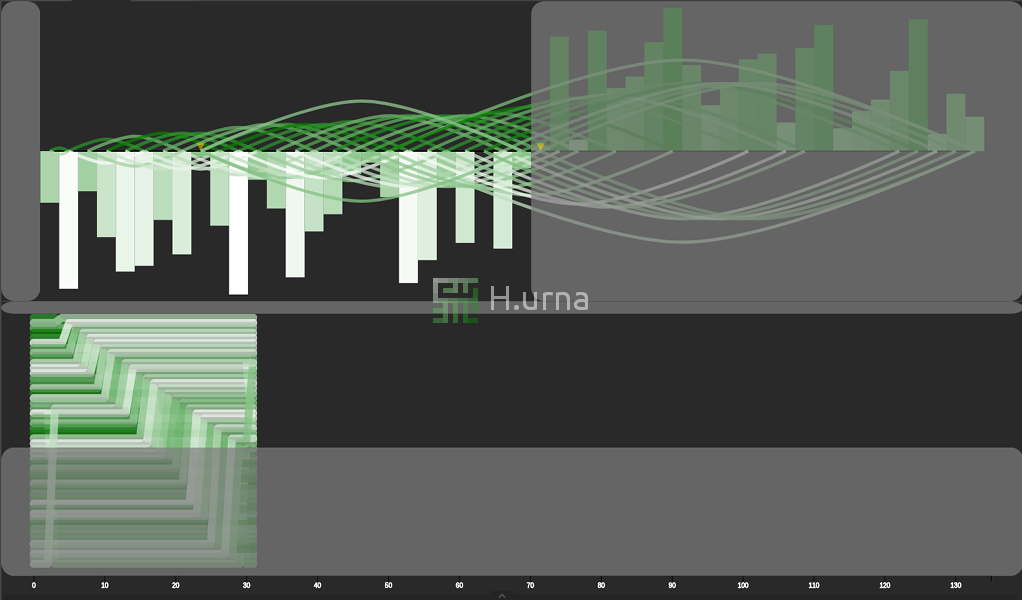
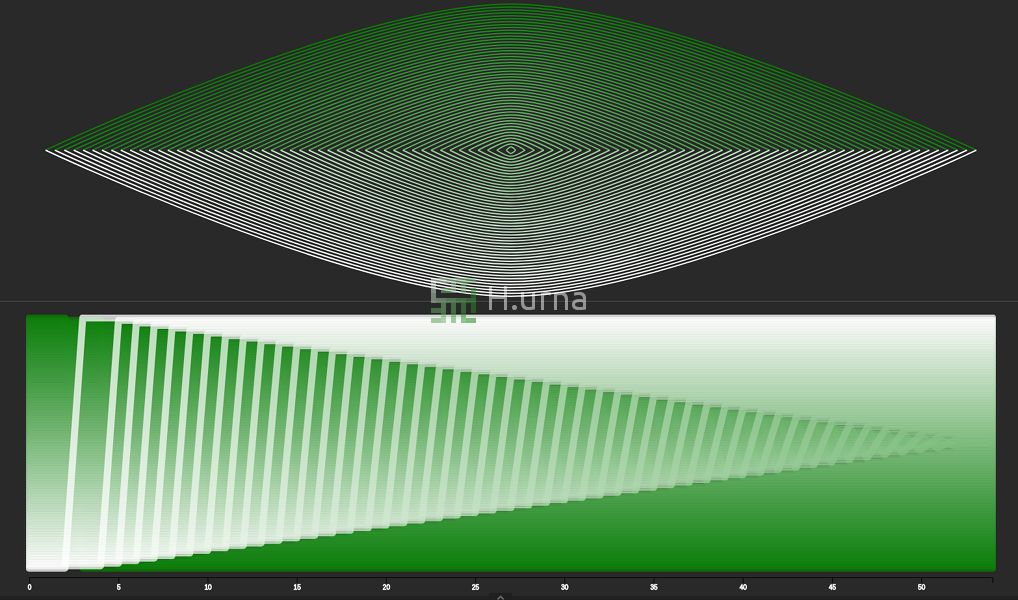
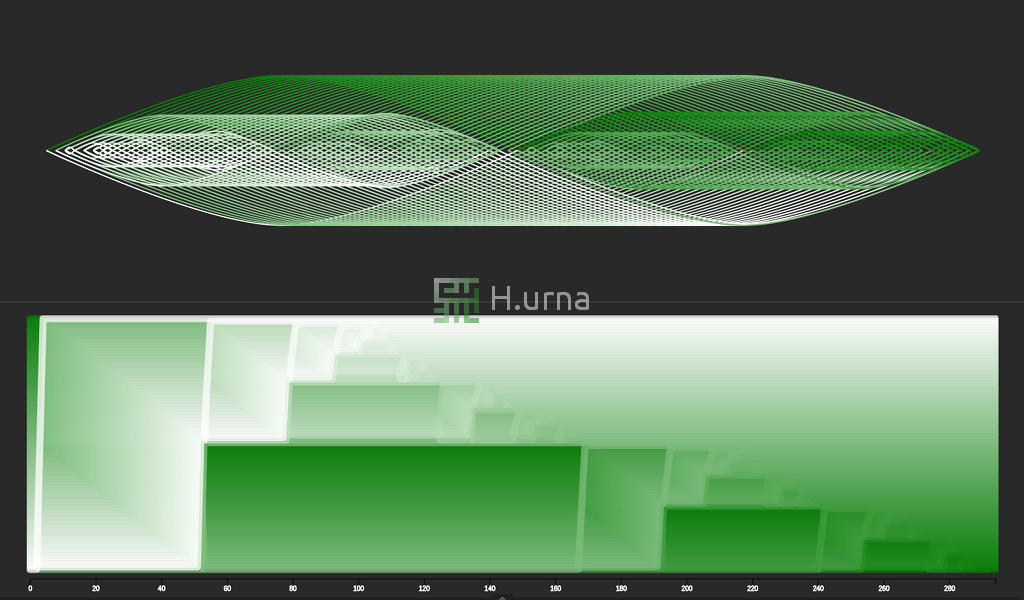
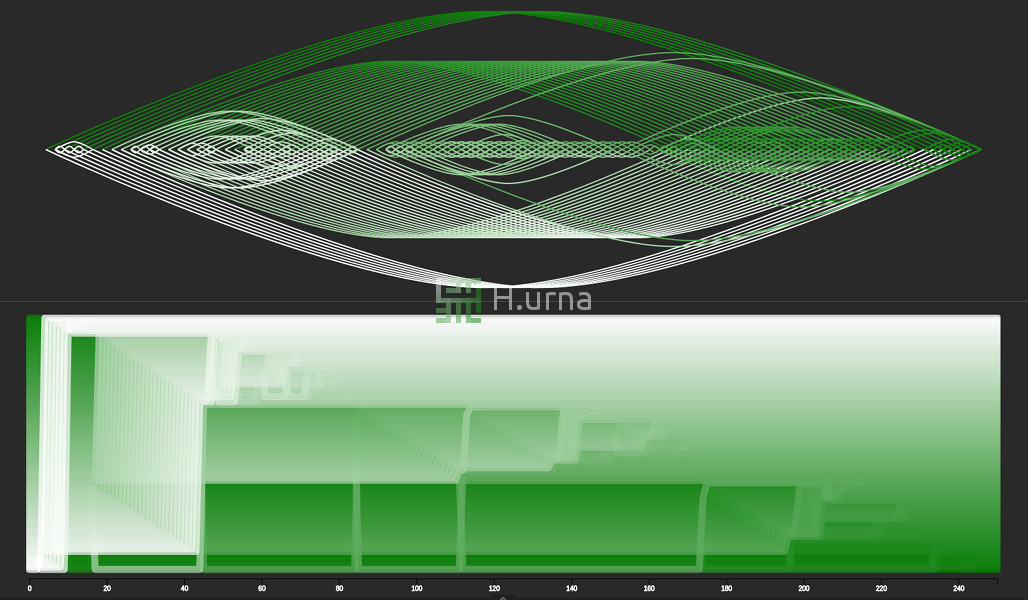
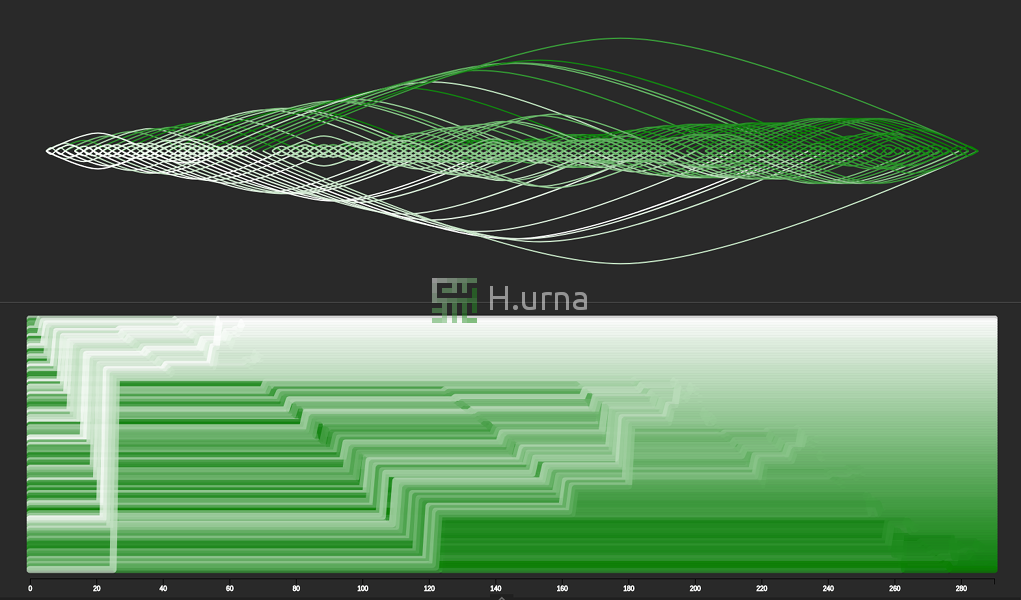
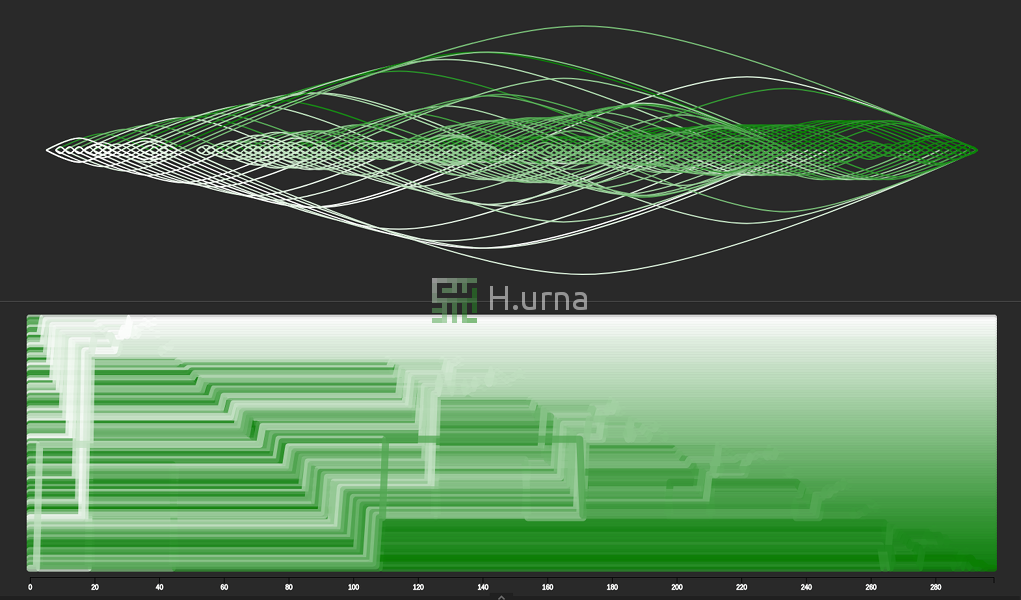
Visualisation
Stratégies de choix du pivot
L'algorithme choisit un élément comme pivot et partitionne la séquence en fonction de celui-ci. Cette sélection du pivot peut être faite de plusieurs manières et ce choix peut grandement affecter les performances de l'algorithme. Voici quelques unes des stratégies possibles:
- Toujours choisir le premier élément.
- Toujours choisir le dernier élément.
- Toujours choisir l'élément du milieu.
- Choisir un élément au hasard.
- Choisir la valeur médiane (basée sur trois éléments).
Comparons visuellement ces stratégies dans deux conditions initiales différentes : une séquence décroissante et une séquence aléatoire.
Complexité
Rappel
Le Partitionnement a une complexité temporelle en O(n) et une complexité spatiale en O(1) dans tous les cas.
Théorèmes mathématiques utiles:
| Sommes | Théorème principal pour les récurrences (Divide and Conquer) |
|---|---|
| $$\sum_{i=0}^{n-1} n = n(n-1)$$ | $$T(n) = O(n) + 2T(\frac{n}{2}) \quad-->\quad O(n log n)$$ |
| $$\sum_{i=0}^{n-1} i = \frac{n(n + 1)}{2} - n = \frac{n(n - 1)}{2}$$ | $$T(n) = O(1) + T(\frac{n}{2}) \quad-->\quad O(log n)$$ |
| $$\sum_{i=0}^{n-1} (n+i) = \sum_{i=0}^{n-1} n + \sum_{i=0}^{n-1} i$$ |
Temps
Meilleure
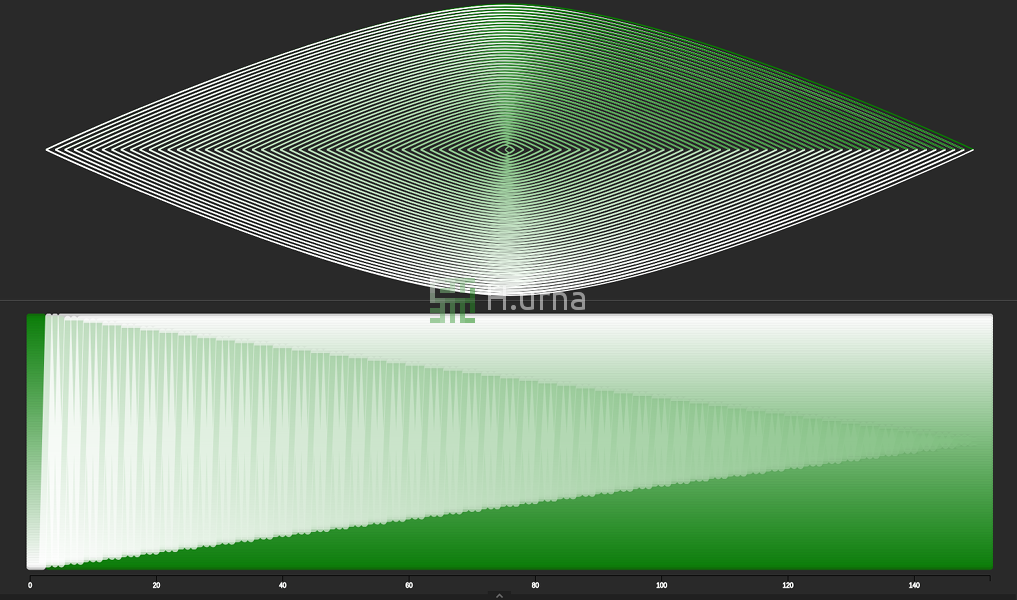
La meilleure situation se produit lorsque chaque partitionnement divise la séquence en deux parties égales (la médiane réele est choisie). Cela signifie qu’après la première partition, chaque appel récursif traite une séquence de la moitié de la taille initiale. Mettons cela dans une relation de récurrence: $$T(n) = O(n) + T(\frac{n}{2}) + T(\frac{n}{2})$$ $$T(n) = O(n) + 2T(\frac{n}{2})$$ Avec le théorème principal pour les récurrences de type divide-and-conquer : T(n) = O(n log n).
Pire
La pire situation se produit lorsque chaque partitionnement divise la séquence en deux sous-séquences de tailles 1 et n - 1 (la plus petite ou la plus grande valeur est choisie). Par conséquent, il y aura ensuite n - 1 partitionnements:
Séquences
$$a_0 = n$$ $$a_1 = n - 1$$ $$a_2 = n - 2$$ $$...$$ $$a_i = n - i$$
Calcul
$$S(n) = \sum_{i=0}^{n-1} (n-i)$$ $$S(n) = \sum_{i=0}^{n-1} n - \sum_{i=0}^{n-1} i$$ $$S(n) = n(n - 1) - \frac{n(n - 1)}{2}$$ $$S(n) = \frac{n(n - 1)}{2}$$ $$S(n) = k(n^2 - n)$$ $$S(n) \approx O(n^2)$$
Cela se produit par exemple en utilisant le dernier élément comme pivot dans une séquence décroissante.
Mémoire
Rappel: - Le partitionnement nécessite O(1) d'espace mémoire. - Les récursions sont ici faites les unes après les autres. Ceci est appelé récursion de queue et signifie que celle de droite commence seulement après que celle gauche ai terminé son processus. Cela implique que la récursion de droite ne s'ajoute pas à la pile d'appels (de fonctions) de celle de gauche.
Meilleure
Comme nous l'avons vu avec la complexité temporelle, chaque appel récursif traite une liste de moitié dans ce cas. Mettons cela dans une relation de récurrence pour l'utilisation de la pile d'appels et utilisons à nouveau le théorème principal pour les récurrences: $$T(n) = O(1) + T(\frac{n}{2})$$ --> O(ln n) en utilisation de la pile d'appels des fonctions (call stack).
Pire
Comme nous l'avons vu, il y a n − 1 appels imbriqués --> O(n) en utilisation de la pile d'appels des fonctions (call stack).
Parallélisation
Après que le tableau ai été partitionné une première fois, les deux sous-séquences peuvent être triées en parallèle.
Le tri Rapide présente certains inconvénients par rapport aux algorithmes de tri alternatifs tels que le tri par fusion. La profondeur de la pile d'appel des récursions affecte directement l'évolutivité de l'algorithme, et cette profondeur dépend fortement du choix du pivot.


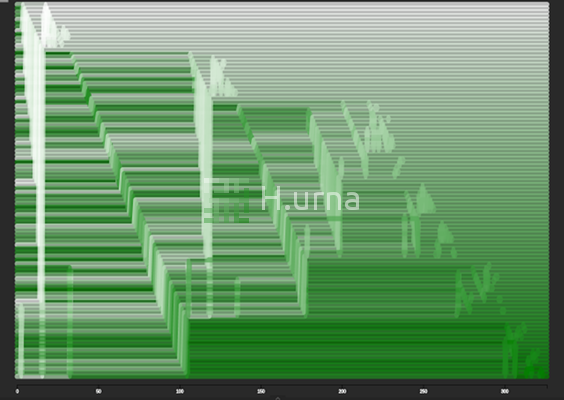

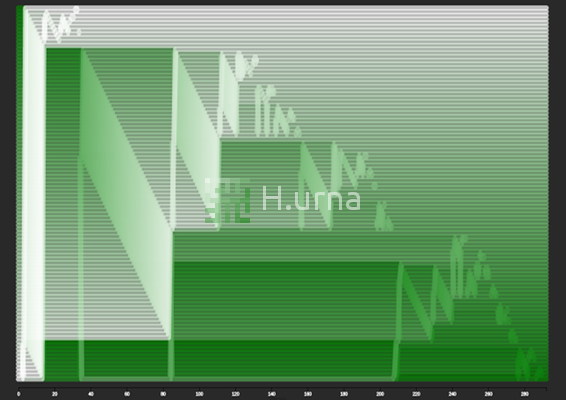
 Jouer en ligne
Jouer en ligne
 Code Source C++
Code Source C++