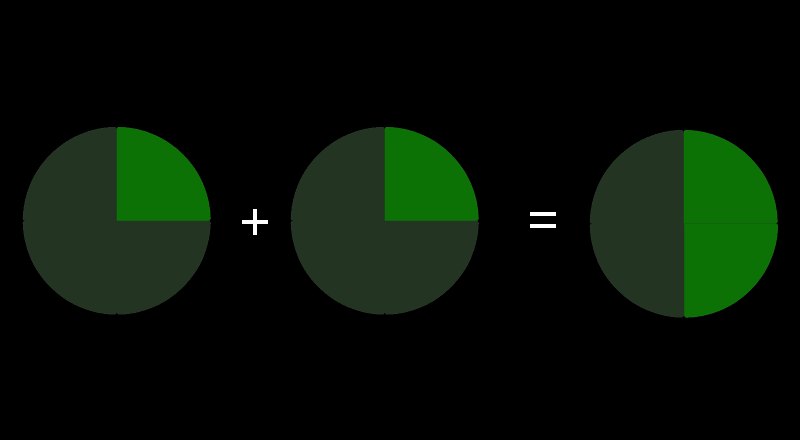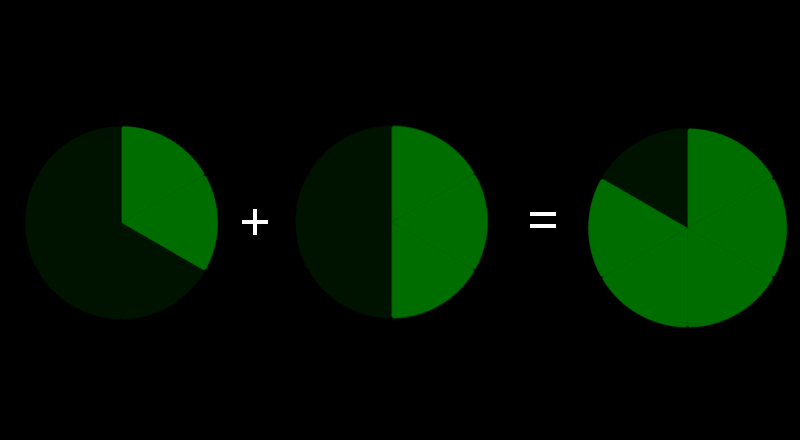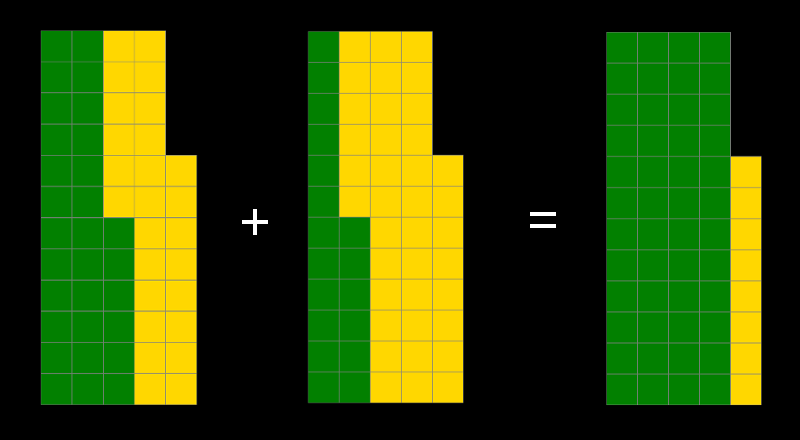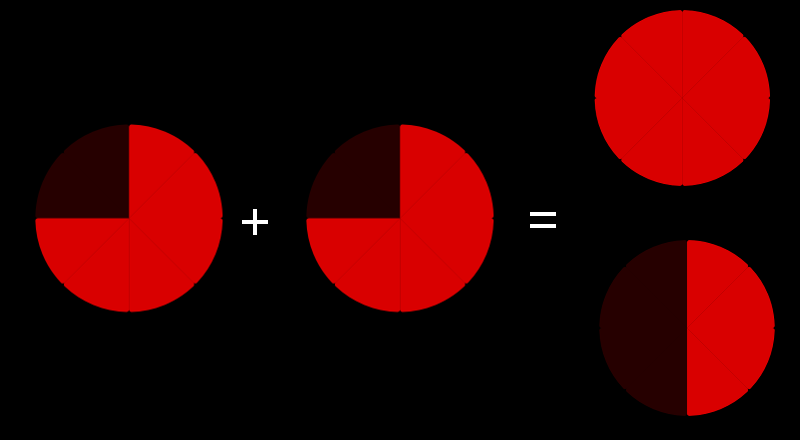L'addition et la soustraction de fractions peuvent sembler délicates au début, mais si nous suivons quelques étapes simples, nous comprendrons cela très rapidement. Néanmoins, nous recommandons de commencer par le cours 'simplifier une fraction’ si nous ne l’avons pas déjà lu ;)

Après ce cours, nous pourrons, entre autres choses:
1. Mieux comprendre et manipuler les fractions.
2. Ajouter ou soustraire des fractions simples.
3. Transformer une fraction en une autre équivalente.
4. Ajouter ou soustraire des fractions avec différents dénominateurs.

Pour commencer: rappel de ce qu’est une fraction et comment elle peut être représentée.

Petit Rappel

Ce qu’il y a au dessus, c’est à dire au numérateur, représente le nombre de parts que l’on prend.
Ce qu’il y a en dessous, c’est à dire au dénominateur, représente le nombre de parts totales.

Si nous multiplions ou divisons le numérateur et le dénominateur d'une fraction par un même nombre : nous obtenons une fraction équivalente (égale).

Nous ne divisons jamais par 0 !

Le signe '-' peut être déplacé où nous le voulons: $$\frac{-a}{b}=-\frac{a}{b}=\frac{a}{-b}$$ $$\frac{-a}{-b}=\frac{a}{b}$$

Le jeu

Lorsque les fractions ont le même dénominateur, il suffit d'ajouter/soustraire les numérateurs et de placer le résultat sur le dénominateur commun. Enfin, nous simplifions la fraction résultante si nécessaire (cf. simplifier une fraction) pour que le résultat soit le plus net possible.

Voyons d’abord quelques exemples simples où les dénominateurs sont les mêmes:

Reprenons notre tarte aux épinards qui était coupée en quatre. Si nous prenons une part, puis une autre: $$\frac{1}{4} + \frac{1}{4} = \frac{1 + 1}{4} = \frac{2}{4} \quad = \quad \frac{1}{2}$$

Cette fois-ci, la tarte arrive coupée en six. Nous sommes au début deux copains à en prendre une part, puis un pote arrive et nous en reprenons une tous ensemble: $$\frac{2}{6} + \frac{3}{6} = \frac{2 + 3}{6} = \frac{5}{6}$$ Nous avons mangé 5/6 de la tarte et il en reste 1/6.

Dans une classe de 56 étudiants, 30 ont de super résultats. Après avoir utilisé H.urna, 18 étudiants arrivent aussi à avoir facilement de super résultats: $$\frac{30}{56} + \frac{18}{56} = \frac{30 + 18}{56} = \frac{48}{56} \quad = \quad \frac{6}{7}$$
Nous savons maintenant que 48 étudiants sur les 56 ont de super résultats. Nous pouvons aussi dire que 6/7 des étudiants ont de super résultats dans cette classe.

Dernier exemple : Cette fois-ci, nous sommes 6 amis ayant commandé 2 pizzas à la tomate sur la route. Chaque pizza est découpée en 8 parts égales (classique). Si chacun de nous mangeons deux parts, combien en mangeons nous au total et combien nous en reste-t-il? $$\frac{6}{8} + \frac{6}{8} = \frac{6 + 6}{8} = \frac{12}{8} \quad = \quad \frac{3}{2}$$
Nous avons mangé 3/2 (ou 1.5) pizzas et il en reste 1/2 (ou 0.5) à partager.
Note: 3/2 + 1/2 = 4/2 = 2 pizzas.

Les choses commencent à devenir intéressantes lorsque les dénominateurs sont différents: cela se produit par exemple lorsqu'un ami apporte une pizza coupée en six alors que nous en avons une coupée en 8. La difficulté consiste uniquement à obtenir le même dénominateur.

Si l’addition ou la soustraction est notre objectif, les chiffres du bas doivent être kif-kif!

Lorsque les fractions ont des dénominateurs différents, il existe plusieurs façons de résoudre le problème. Nous allons voir ici le moyen le plus simple, puis un tour de passe-passe rapide et, enfin, la méthode traditionnelle.

Méthode la plus simple

Pour cette méthode, il suffit de multiplier le numérateur et le dénominateur de chaque fraction par le dénominateur de l'autre; nous appelons cela multiplier les fractions en croix. Attention: cette méthode peut s'avérer inefficace si nous avons à faire de grands nombres.

Utilisons quelques visulisations pour maîtriser totalement le concept :)

Nous mangeons une part d'une pizza coupée en deux et une part d'une pizza coupée en trois (peace): $$\frac{1}{2} + \frac{1}{3} = $$ On commence par multiplier les fractions en croix pour avoir les même dénominateurs.

Les fractions restent égales. $$\frac{1}{2} + \frac{1}{3} = \frac{1 * \pmb{3}}{2 * \pmb{3}} + \frac{1 * \pmb{2}}{3 * \pmb{2}} = \frac{3}{6} + \frac{2}{6} = $$ Ensuite, nous faisons simplement l'arithmétique avec les numérateurs.

$$\frac{1}{2} + \frac{1}{3} = \frac{3 + 2}{6} = \frac{5}{6}$$ Nous avons mangé au total 5/6 d'une pizza (notre unité).

Note: Nous savons donc aussi que sur les 2 pizzas, il en reste 6/6 + 1/6 (ou 7/6).
5/6 + 7/6 = 12/6 = 2 pizzas

Tour de passe-passse

Cette astuce est le moyen le plus rapide d’ajouter une fraction. Cependant, cela ne fonctionne que dans certains cas: lorsqu'un dénominateur est un multiple de l'autre. Dans ces cas, il suffit de multiplier la fraction du plus petit dénominateur pour atteindre l'autre:

Méthode traditionnelle utilisant le PPCM (ou PPCD)

Nous ne devrions utiliser cette méthode qu'en dernier recours car elle peut être assez longue. À moins que ... nous obtenions le facteur commun simplement en regardant les dénominateurs (cela vient avec un peu de pratique).

Le plus petit multiple commun (ou PPCM) est le plus petit nombre divisible par les deux dénominateurs. Supposons que nous voulions ajouter les fractions 3/6 et 12/15, nous trouvons le PPCM en listant leurs multiples et en prenant le premier (plus petit) qu'ils ont en commun:

Donc, 30 est le PPCM de 6 et 15 !. Nous appelons également ce nombre le plus petit dénominateur commun (PPCD), qui est le plus petit dénominateur commun aux deux fractions.

Il suffit maintenant de multiplier chaque fraction par le nombre bleu pour obtenir le même dénominateur: $$\frac{3}{6} + \frac{12}{15} = \frac{3 * \pmb{5}}{6 * \pmb{5}} + \frac{12 * \pmb{2}}{15 * \pmb{2}} = \frac{15 + 24}{30} = \frac{39}{30} \quad = \quad \frac{13}{10}$$

Félicitations!

Toujours trouver rarpidement le PPCM avec Euclide

Pour toujours trouver le PPCM, il faut d'abord avoir le PGCD. Pour cela, nous utiliserons l'algorithme d'Euclide. Pas de panique, ce n’est vraiment pas compliqué ! Il nous suffit juste de savoir diviser un nombre.

La procédure est la suivante :
- Effectuer la division euclidienne du plus grand nombre (noté a) de la fraction sur le plus petit nombre (noté b) et garder le reste (noté r).
- Tant que le reste est différent de 0, nous réitérons la division en remplacant a par b et b par r.

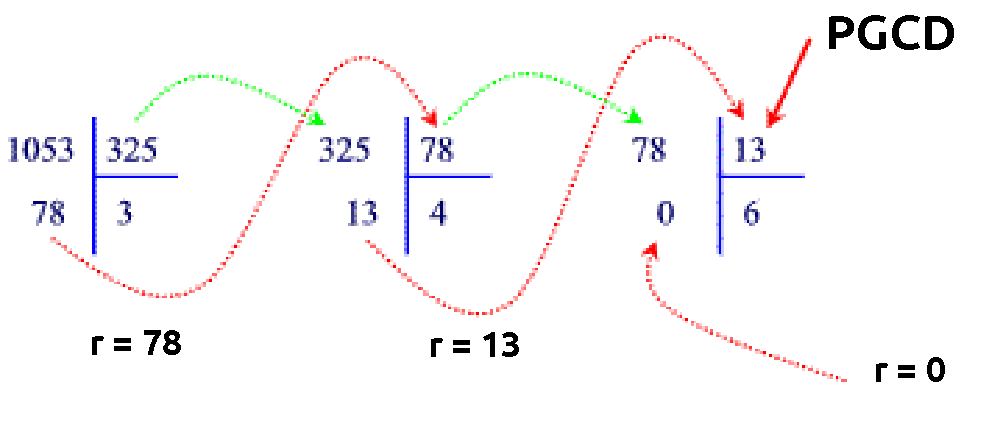
Le PPCM se déduit du PGCD avec la formule suivante: $$PPCM = (a * b) / PGCD(a,b)$$ Dans notre cas, avec 6 et 15 en dénominateurs: $$PPCM = (6 * 15) / PGCD(6,15) = 90 / 3 = 30$$ Sweet... !

En bref

Pour ajouter des fractions, il y a trois étapes:
1. S'assurer que les nombres du bas (les dénominateurs) sont les mêmes.
2. Faire le calcul avec les chiffres du haut (les numérateurs) et placer le résultat sur le dénominateur commun.
3. Simplifier la fraction si nécessaire.

Nous pouvons maintenant ajouter ou soustraire toutes les fractions! Utiliser librement Globo et ses explications pour résoudre vos exercices.
Voici aussi quelques outils pour aller plus loin dans la maîtrise de ce vaste monde fractionnaire.

Tools - Cheatsheets