Multiplier ou diviser des fractions est aussi simple qu'une multiplication normale. Pour multiplier les fractions : nous multiplions les numérateurs entre eux et les dénominateurs entre eux. C'est aussi simple que ça!

Exemple

$$\frac{2}{5} × \frac{1}{3} = \frac{2*1}{5*3} = \frac{2}{15}$$

Lorsque nous additionnons ou soustrayons des fractions, les fractions doivent avoir les mêmes dénominateurs; pour les multiplications et les divisions, peu importe.

Simplification

N'oublions pas de simplifier les fractions d’abord afin de rendre le problème plus facile à résoudre.

Par exemple: $$\require{cancel} \frac{3}{15} × \frac{2}{6} = \frac{\cancel{3} \cdot 1}{\cancel{3} \cdot 5} * \frac{\cancel{2} \cdot 1}{\cancel{2} \cdot 3} = \frac{1}{5} * \frac{1}{3}$$ Est facile à calculer $$\frac{1}{5} * \frac{1}{3} = \frac{1 * 1}{5 * 3} = \frac{1}{15}$$ Contrairement aux fractions initiales $$\frac{3}{15} × \frac{2}{6} = \frac{3 * 2}{15 * 6} = \frac{6}{90} = \frac{\cancel{6} \cdot 1}{\cancel{6} \cdot 15} = \frac{1}{15}$$

Ensuite, n'oublions pas de simplifier la fraction résultante si elle doit être.

Attention aux signes négatifs

Assurons-nous que nous portons ces signes négatifs dans nos calculs.

Le signe '-' peut être déplacé où nous le voulons: $$\frac{-a}{b}=-\frac{a}{b}=\frac{a}{-b}$$ $$\frac{-a}{-b}=\frac{a}{b}$$

Exemple

$$\frac{-2}{5} × \frac{1}{-3} = \frac{-2*1}{-5*3} = \frac{-2}{-15} = \frac{2}{15}$$

Si nous savons multiplier par fractions, nous savons diviser par fractions. Il suffit d'inverser la deuxième fraction et de la multiplier .

Diviser par 1/4.

Revient à multiplier par 4/1.

Donc si nous avons: $$\frac{1}{2} / \frac{1}{4}$$ Qui revient à écrire: $$\frac{1}{2} / \frac{1}{4} = \frac{\frac{1}{2}}{\frac{1}{4}}$$

Nous inversons: $$\frac{1}{2} / \frac{1}{4} = \frac{1}{2} * \frac{4}{1}$$ Puis: $$\frac{1}{2} * \frac{4}{1} = \frac{1 * 4}{2 * 1} = \frac{4}{2} = 2$$

C'est tout. Nous savons maintenant comment multiplier et diviser toutes les fractions !

Petit rappel

Ce qu’il y a au dessus, c’est à dire au numérateur, représente le nombre de parts que l’on prend.
Ce qu’il y a en dessous, c’est à dire au dénominateur, représente le nombre de parts totales.

Nous ne divisons jamais par 0 !

Multiplication

Multiplier une fraction, c'est prendre une fraction de fraction. Pourquoi la solution est-elle un nombre inférieur aux fractions impliquées dans une multiplication ?

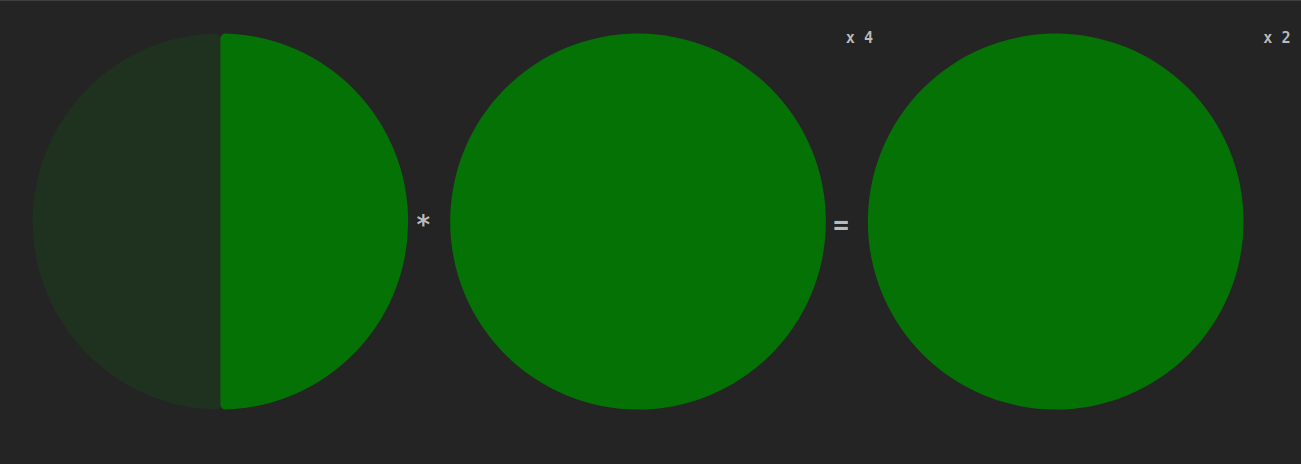
Lorsque nous multiplions une fraction, nous coupons le résultat de la première fraction par «le dénominateur de la deuxième fraction». Puis, nous prenons un nombre de part égal au numérateur de la deuxième fraction.

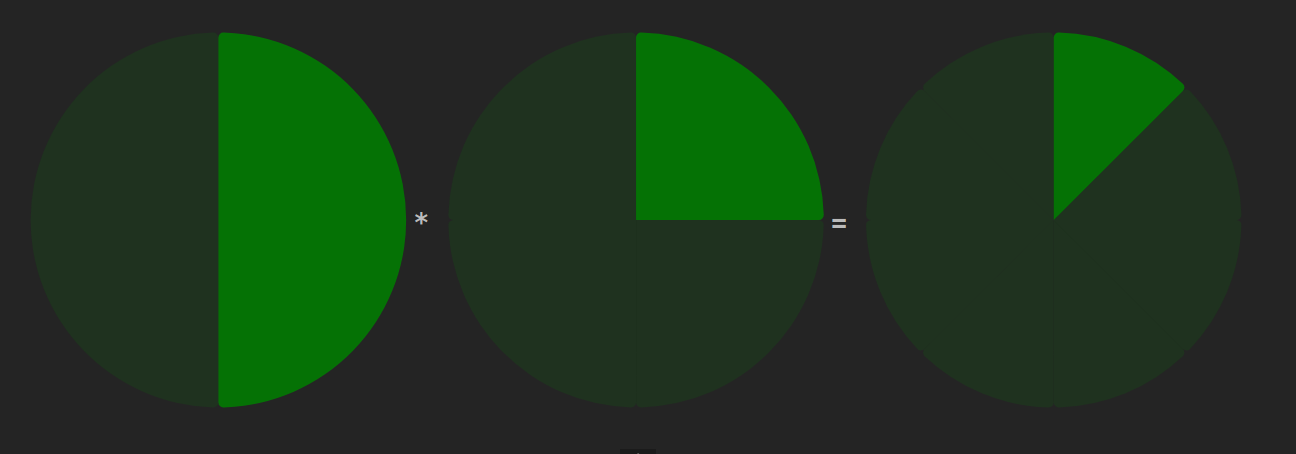
$$\frac{1}{2}*\frac{1}{4}=\frac{1}{8}$$ Si nous coupons la moitié du tout en quatre parties : chaque partie représente maintenant 1/8 du tout.

Division

Pourquoi la solution est-elle un nombre supérieur aux fractions impliquées dans une division ?

Lorsque nous divisons une fraction, nous inversons la logique. Nous demandons combien nous avons au total si nous avons «dénominateur de la seconde fraction» parts de la première fraction. Ensuite, nous coupons ce montant en «numerateur de la seconde fraction» parts.

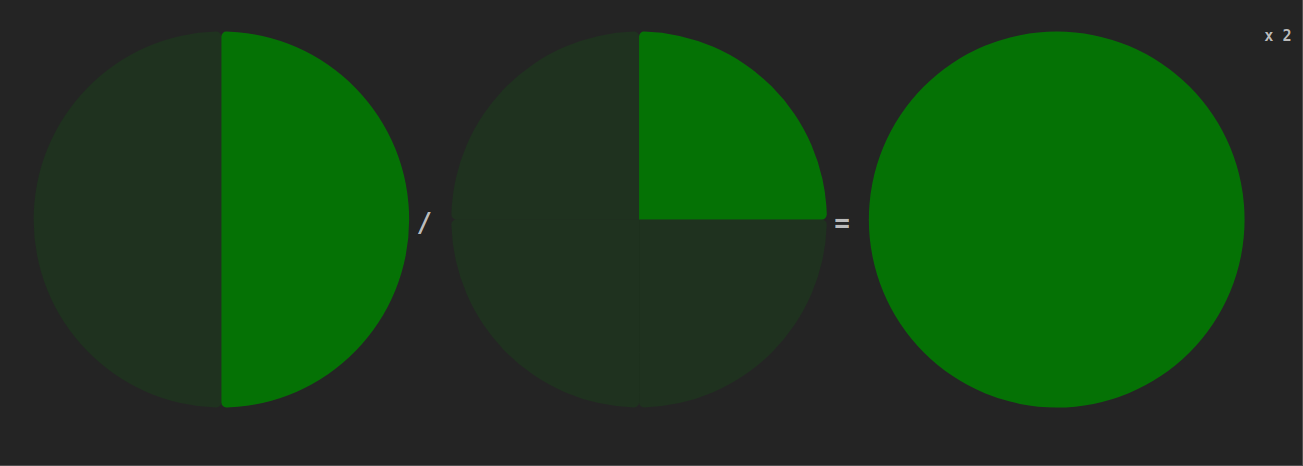
Avec cet exemple: $$\frac{1}{2}/\frac{1}{4}=\frac{1}{2}*\frac{4}{1}=\frac{1*4}{2*1}=\frac{4}{2}=2$$

Nous avons pris 4 fois la moitié d'une pizza. Cela signifie que nous avons pris 2 pizzas entières.