L’intégration est l’une des deux opérations principales des mathématiques avec son opération inverse : la dérivation. L'intégral est, en mathématiques, soit une valeur numérique égale à l'aire sous la courbe (zone entre abscisse et graphique) d'une fonction pour un intervalle (intégrale définie) ou une fonction F(x) inverse de la dérivée (intégrale indéfinie) : trouver une intégrale est l'inverse de la recherche d'un dérivé, c'est pourquoi on l'appelle aussi parfois l'anti dérivée.

Les intégrales illustrées ici sont celles dites intégrales définies : une valeur numérique égale à l'aire sous la courbe entre deux points A et B (intervalle fermé) donnée par : $$\int _{a}^{b}\,f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a)$$

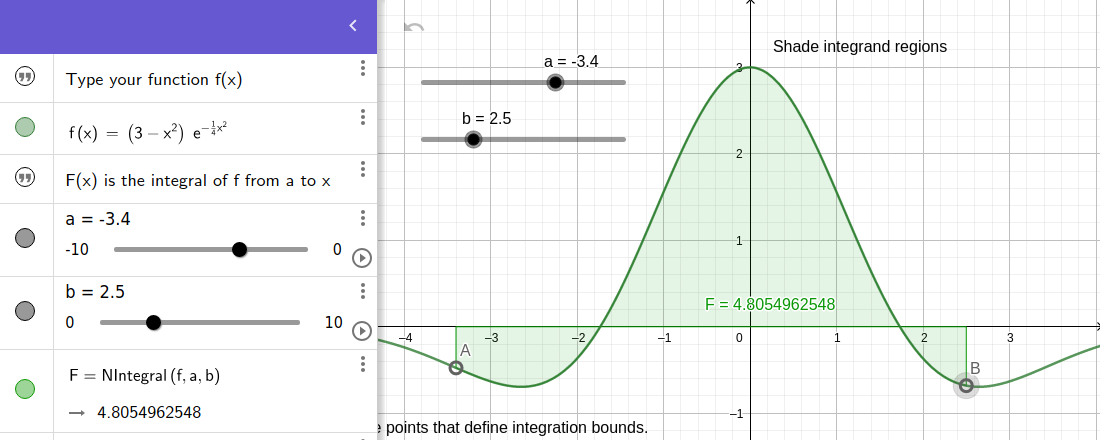
L'opération d'intégration menant à F(x) ajoute une constante qui peut être ce que l'on veut, en effet :
$$f(x) = k → f’(x) = 0, \quad donc$$ $$f(x) = 0 → F(x) = constante$$ Dans ce cas, c’est la fonction qui fait référence à une intégrale indéfinie et qui est simplement écrite : $$F(x)=\int f(x)\,dx$$

En d'autres termes, la constante peut être n'importe valeure pouvant exister avant le point A et donc le point B, l'intégrale définie annule cette quantité lors de la soustraction : $$F(b) - F(a)$$

Jouons avec eux

Sautons à bords de Hurna Explorer pour manipuler toutes ces fonctions.