Integration is one of the two main operations of calculus with its inverse operation : differentiation. The Integral is, in mathematics, either a numerical value equal to the area under the curve (area between abscissa and graph) of a function for some interval (definite integral) or a function F(x) inverse to the derivative (indefinite integral) : finding an integral is the reverse of finding a derivative, this is why it is also called the antiderivative.

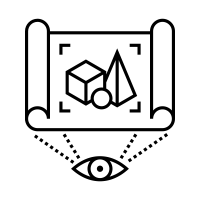
The integrals illustrated here are those termed definite integrals: a numerical value equal to the area under the curve between two point A and B (closed interval) and is given by : $$\int _{a}^{b}\,f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a)$$

The operation of integration leading to F(x) is up to an additive constant, indeed :
$$f(x) = k → f’(x) = 0, \quad thus$$ $$f(x) = 0 → F(x) = any_{constant}$$ In this case, This is the function that refers to an indefinite integral and is simply written : $$F(x)=\int f(x)\,dx$$

In other words the constant may be any area offset that may exist before point A, and therefore point B, the definite integral cancel this quantity during subtraction: $$F(b) - F(a)$$