La tangente en un point de la courbe est la droite (fonction linéaire) qui traverse ce point et a la même pente que celle de la courbe en ce point (son coefficient directeur = f'). Bien que la tangente puisse être calculée point par point, c'est «heureusement» un produit direct de notre dérivé f’(x):
$$ tangent_{ligne}(x) = f'(a)(x-a) + f(a)$$

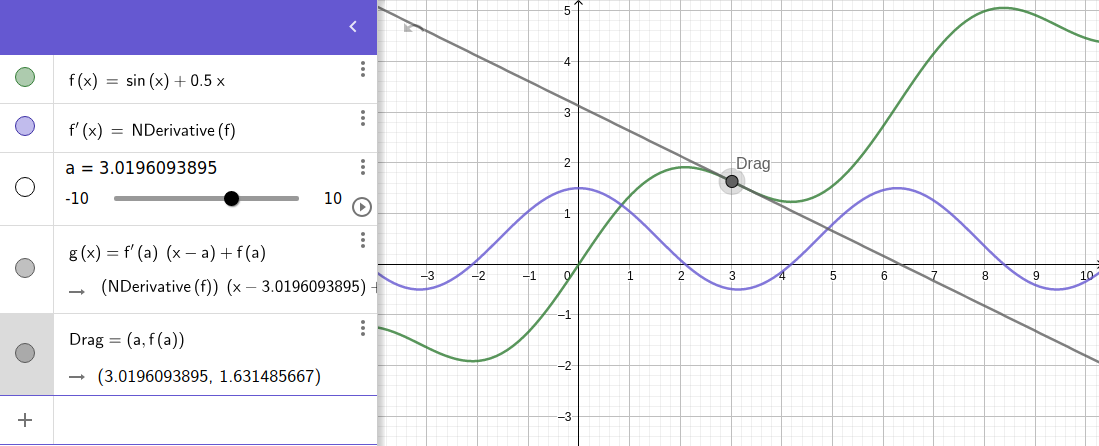
L'équation linéaire de la ligne tangente peut être lue comme suit :
$$tangent_{line}(x) = ax + b$$ La constante a est f’(a) : la pente de la courbe au point A.
La constante b est f(a) : la valeur de la courbe au point A (son offset).
La variable x est (x - a) : nous avons simplement déplacé l'origine de l'abscisse de la ligne tangente au point A (cf. translation fonction plus haut).