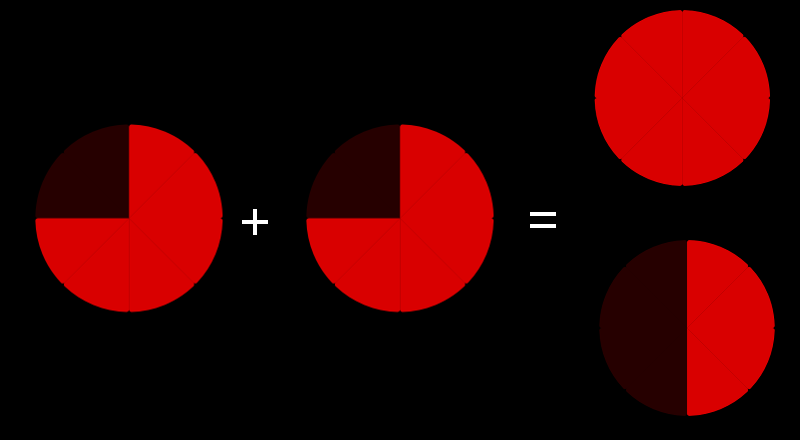Quick Access
Introduction
Whatever we do in life, we manipulate fractions on a daily basis. This is done for example when we cut a pie, read a percentage on a label or play LEGO.
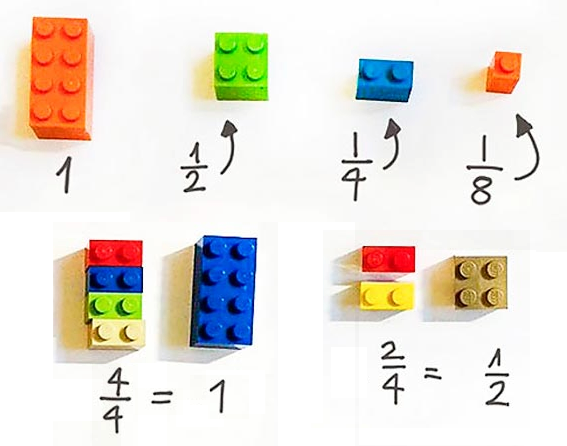
Fractions are also the first abstract concept taught in mathematics and more often what confuses students with mathematics. Although these may seem tricky at first, it becomes much simpler once we visualize what a fraction is and how it works.
Taking a Fraction
The number above, at the numerator, represents the number of shares we take. The number below, at the denominator, represents the number of total shares.
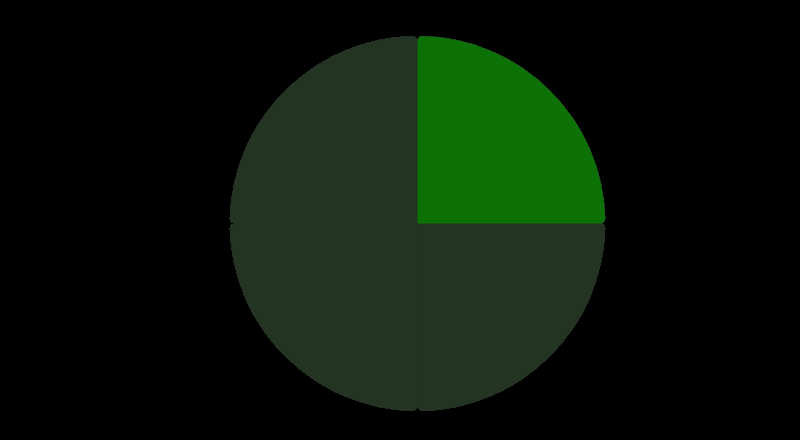
If we take 1/4 (a quarter) of a pie, we cut it into 4 equal parts and take 1 share.
Other concrete examples:
- If in a class of 16 students 9 are girls, then 9/16 of them are girls.
- To advance 3/4 of a meter, we divide it into 4 equal steps (of 25cm)
then advance of 3 times this distance (75cm).
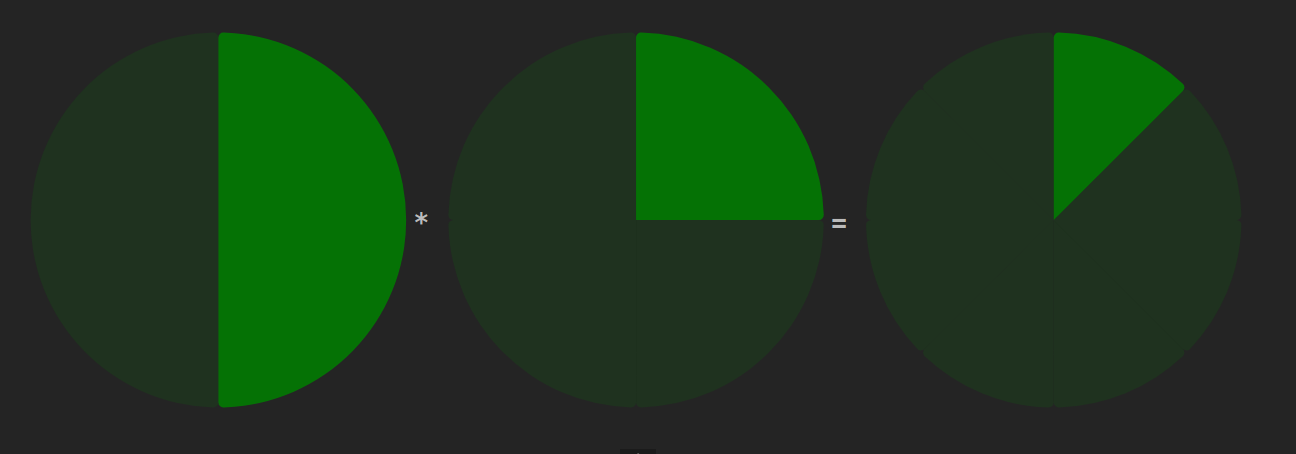
- To take 3/5 of a number, we divide by 5 and multiply by 3.
Two main rules
We never divide by 0!
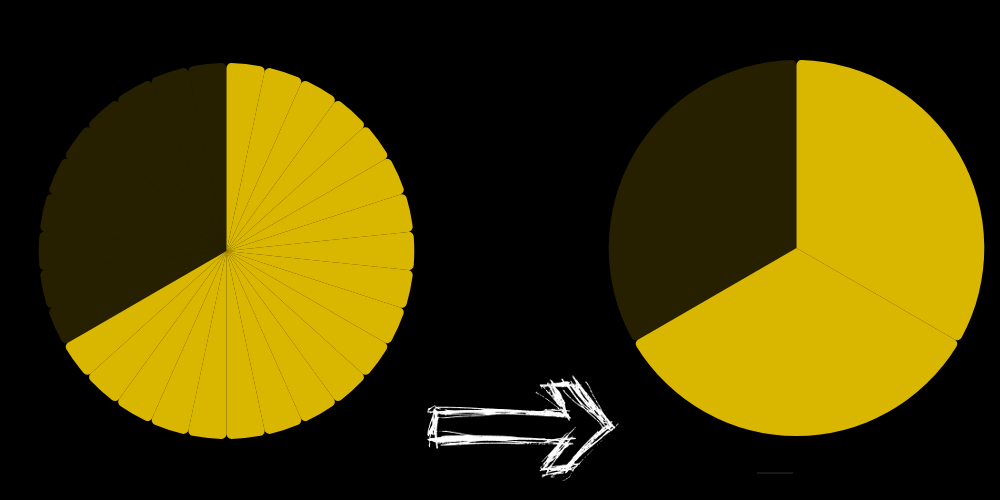
If we multiply or divide the numerator and the denominator of a fraction by the same number: we get an equivalent fraction (equal).
Objectives
We may want to visualize and manipulate fractions first. Let's use the H.urna Explorer
Tools - Cheatsheets
|
|

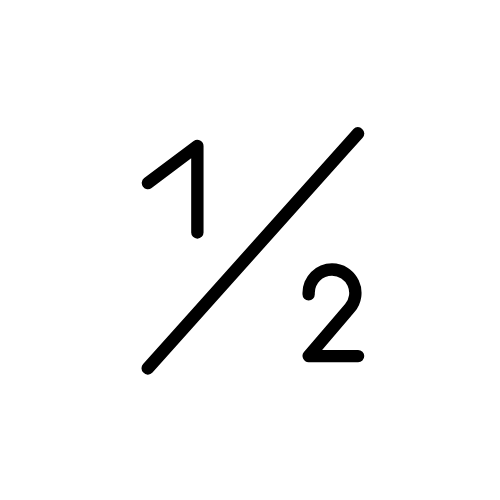 Simplify
Simplify
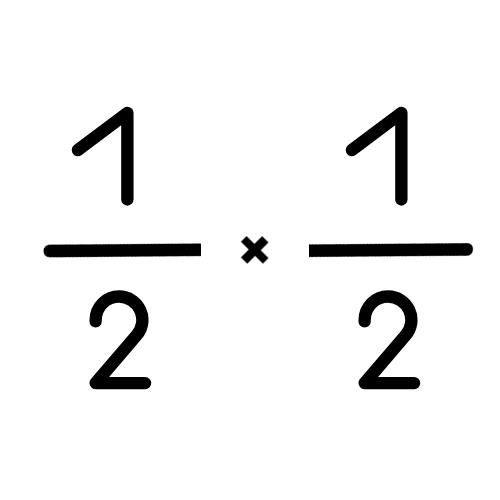 Multiply &
Divide
Multiply &
Divide
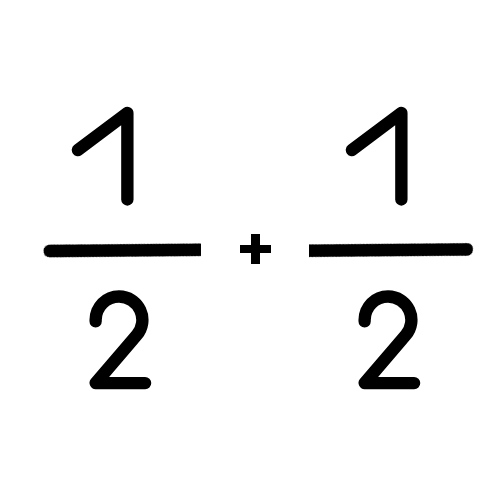 Add &
Subtract
Add &
Subtract
 Worksheets
Worksheets
 Play online
Play online
 Step-by-step simpliflier
Step-by-step simpliflier