Arithmetic sequences are a good starting point for understanding other types of sequences. However, I recommend to quickly read the introductory course on the suites and the one on the direction of variation of a sequence if you haven't already ;)

It will be much simpler here, an arithmetic sequence is just a special case that is very easy to identify. Here is its definition:

$U_{n}$ is an arithmetic sequence if there exists a number $r$ such that, for all $n\in \mathbb{N}$: $$U_{n+1}=U_{n} + r$$ The real number r is called the common difference of the arithmetic sequence.

Ok, but is there a way to make it clearer ?!

With an arithmetic sequence, we always add the same (constant) value between two consecutive terms. It is this recurrence relation that defines all arithmetic progression.

Be careful however, the added value r is constant but can be negative.

Let's start by identifying the case in which we are handling an arithmetic sequence.

If we have already read the course concerning the direction of variation of a sequence, we may remember that finding the recurrence relation between two terms is equivavlent to calculating the difference between these two terms . In the same way, we will calculate here $U_ {n + 1} - U_n$ to see if this difference is constant (if we always add the same value). In other words:

If $U_{n+1} - U_n = r$ where r is a real (therefore a constant), then the sequence is arithmetic with common difference r.

Indeed, written differently, we find back our definition: $$U_{n+1} = U_n + r$$

Conversely, if $U_ {n + 1} - U_n$ is not equal to a constant, we can conclude that the sequence $U_n$ is not arithmetic.

Some of you may already have the graphic representation in mind. With an arithmetic sequence we always add the same value, it is exactly like in a staircase; with r, the number of steps you go up or down at each step.

If we calculate the first three terms of our sequence $U_n = -3n + 4$:

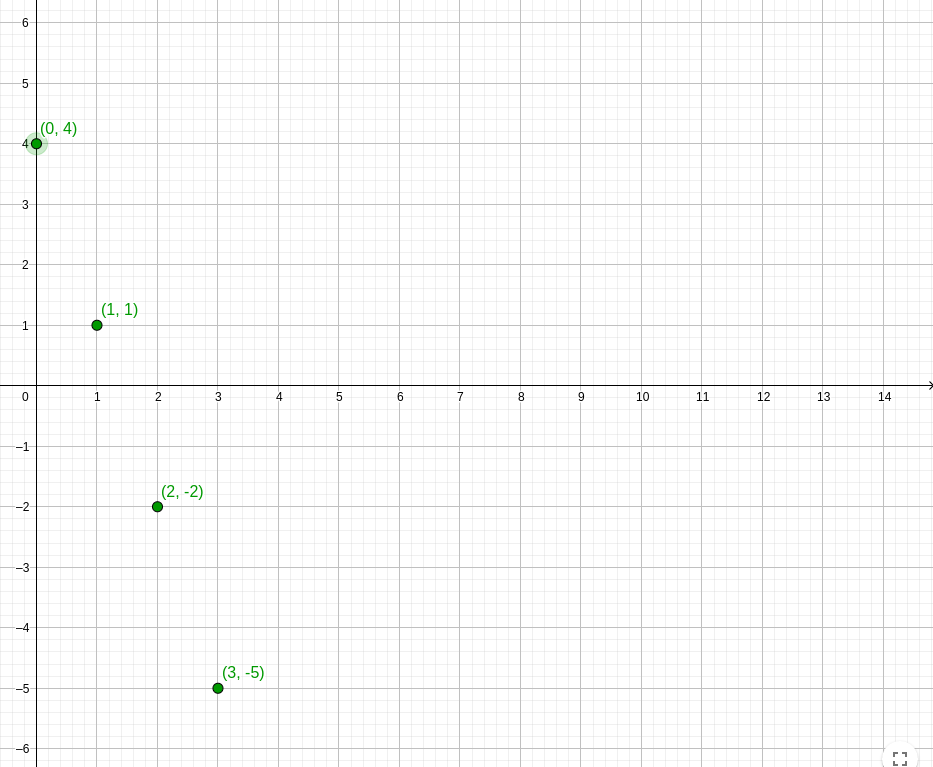
We go down the stairs three by three (watch your ankle ...).

Let's take this opportunity to draw a parallel with the functions. We replace $n$ with $x$, and $U_n$ with $f(x)$: $$U_n = -3n + 4$$ $$f(x) = -3x + 4$$

I know this; affine or linear function kinda things?
Exact. An arithmetic sequence is an affine function defined only for particular points.

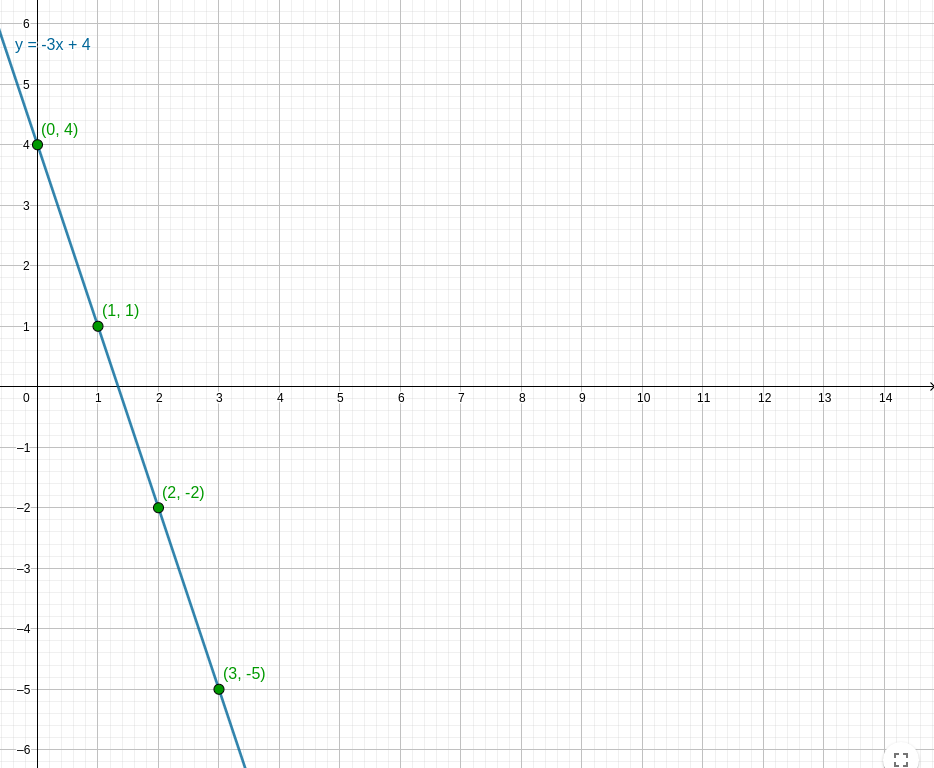
We can clearly see here the link between an arithmetic sequence and an affine function: $$f(x) = ax + b$$ $$U_n = an + b$$ We find 'a' as the directing coefficient and 'b' as the initial value (offset). The following property will finish illustrating this link ^^

If a and b are two real numbers and if the sequence $U_ {n}$ is defined by: $$U_{n}=a \times n+b$$ then this sequence is an arithmetic sequence with common difference $r = a$ and of first term $U_{0} = b$.

At this stage, this chapter hardly deserves to exist :D
Let us recall this property:

If $U_{n+1} - U_n = r$ where r is a real (therefore a constant), then the sequence is arithmetic with common difference r.

The following theorem then becomes obvious (well, you still have to have read the course about the direction of variation of a sequence):

Let $U_ {n}$ be an arithmetic sequence with common difference r:

If r > 0 then $U_{n}$ is strictly increasing.
If r < 0 then $U_{n}$ is strictly decreasing.
If r = 0 then $U_{n}$ is constant.

That's all?
Yup!

Cool! We will now end this course with two super important things:
- Guess the relation $U_n$ as a function of n.
- Calculate the sum of an arithmetic sequence, as:
1 + 2 + 3 + 4 + ... + 100 =? (admit that we all want to know how to answer that in 2 seconds ^^).

Let's go for this.

So, guys, how can we calculate $U_ {10}$ from an arithmetic sequence directly?

Easy man, you told us that we always add the same thing. So $U_ {10}$ that's what we had at the start + 10 pays: $U_ {10} = U_0 + 10r$. You have even already dropped the formula with $U_n = b + an$.

Straightforward ... Let's do the reasoning anyway, this is the kind of thing that will be regularly asked and it allows us to find the explicit form of many suites.

We will consider knowing only the recurrence formula: $$U_{n+1}=U_{n} + r$$ The idea will be to find the explicit form, $U_n$ as a function of n.

After you...
It is like in the logic games "find the logical continuation of this series" or "find the missing number in this sequence". How? Let's start by calculating the first terms $U_0, U_1, U_2, U_3$:

$U_{0}$ (initial term)
$U_{1} = U_{0} + r$ (Ok)

$U_{2} = U_{1} + r$ (replace with $U_{1}$)
$\quad = (U_{0} + r) + r$
$\quad = U_{0} + 2r$

$U_{3} = U_{2} + r$ (replace with $U_{2}$)
$\quad = (U_{0} + 2r) + r$
$\quad = U_{0} + 3r$
...

We can clearly see the pattern $U_n = U_0 + nr$
Yep. Now that we have that, we're gonna get the hang of it and use our mega technique. Little reminder:

Sometimes the sequences do not start at 0.
We can define a sequence "For all n ≥ 3". In that case $U_{0}$, $U_{1}$ and $U_{2}$ do not exist; we calculate the terms starting from $U_{3}$.

So, what happens to the explicit form if we no longer start from 0?
...

This time we will want to express $U_n$ in terms of another term that is not $U_0$, let's say $U_p$.

You keep telling us that to calculate the difference between two terms is equivalent to define their relationship. We do this, right?
Bingo.

$$U_n = U_0 + n \times r$$ $$U_p = U_0 + p \times r$$
$$U_n - U_p = (U_0 + nr) - (U_0 + pr)$$ $$\quad = U_0 + n \times r - U_0 - p \times r$$ $$\quad = (n - p) \times r$$
We have just found the general explicit form of all arithmetic sequences!
We can conclude:

If the sequence $U_ {n}$ is arithmetic of with common difference r then for all natural numbers n and p:
$$U_n = U_p + (n - p) \times r$$

Go to last section, we will finally calculate 0 + 1 + 2 + 3 + ...

Last mad technique of this course. To calculate the sum "S = 0 + 1 + 2 + 3 + ... + n", we are going to write it once in order and once upside down:

$(a) \quad S = \color{darkred}{0} + \color{goldenrod}{1} + \color{darkgreen}{2} + \cdots + \color{darkblue}{n}$
$(b) \quad S = \color{darkred}{n} + \color{goldenrod}{n - 1} + \color{darkgreen}{n - 2} + \cdots + \color{darkblue}{n - n}$

Now we add (a) + (b):

$(a + b) \quad 2S = \color{darkred}{n} + \color{goldenrod}{n} + \color{darkgreen}{n} + \cdots + \color{darkblue}{n}$

WARNING: If the sum goes from 0 to n, there are n + 1 terms!
For instancec, from 0 to 4, there is 0, 1, 2, 3, 4, which is 5 terms.

Therefore:
$2S = n * (n + 1)$

To conclude:
$$S = \frac{n * (n + 1)}{2}$$

THEOREM (SUM OF FIRST INTEGERS)
For all natural number $n \in \mathbb{N}$: $$0 + 1 + 2 + \cdots + n = \frac{n * (n + 1)}{2}$$

Then, how much is $0 + 1 + 2 + \cdots + 100$?
$S_{100} = \frac{100 * 101}{2} = \frac{10100}{2} = 5050$

Bad Ass Style

You will discover the notation that you will find everywhere in mathematics, the sigma sum: $\sum_{n=0}^{n}$. It sounds super complicated, but in fact it's nothing but Sn! What is underneath is where we start and above where we finish. We can thus rewrite our theorem:

THEOREM (SUM OF FIRST INTEGERS)
For all natural number $n \in \mathbb{N}$: $$\sum_{n=0}^{n} n = \frac{n * (n + 1)}{2}$$

General Formula

Are you still going to give us the formula that works for all arithmetic sequences?

Let Sn be the sum of all the terms of an arithmetic sequence between rank p and rank n (p < n): $$Sn = (n − p + 1) ∗ \frac{U_p + U_n}{2}$$

Here is a visual way to remember this formula (the sum is like the area).

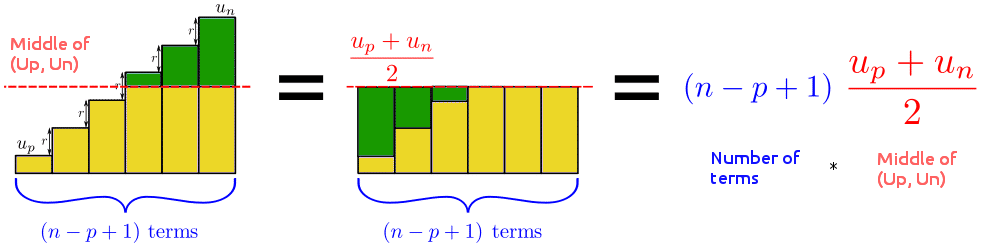
For the more motivated, I suggest that you demonstrate it yourself to master this course.

$U_{n}$ is an arithmetic sequence if there exists a number $r$ such that, for all $n\in \mathbb{N}$: $$U_{n+1}=U_{n} + r$$ The real number r is called the common difference of the arithmetic sequence.

If $U_{n+1} - U_n = r$ where r is a real (therefore a constant), then the sequence is arithmetic with common difference r.

Conversely, if $U_ {n + 1} - U_n$ is not equal to a constant, we can conclude that the sequence $U_n$ is not arithmetic.

If a and b are two real numbers and if the sequence $U_ {n}$ is defined by: $$U_{n}=a \times n+b$$ then this sequence is an arithmetic sequence with common difference $r = a$ and of first term $U_{0} = b$.

Let $U_ {n}$ be an arithmetic sequence with common difference r:

If r > 0 then $U_{n}$ is strictly increasing.
If r < 0 then $U_{n}$ is strictly decreasing.
If r = 0 then $U_{n}$ is constant.

Sometimes the sequences do not start at 0.
We can define a sequence "For all n ≥ 3". In that case $U_{0}$, $U_{1}$ and $U_{2}$ do not exist; we calculate the terms starting from $U_{3}$.

If the sequence $U_ {n}$ is arithmetic of with common difference r then for all natural numbers n and p:
$$U_n = U_p + (n - p) \times r$$

THEOREM (SUM OF FIRST INTEGERS)
For all natural number $n \in \mathbb{N}$: $$0 + 1 + 2 + \cdots + n = \frac{n * (n + 1)}{2}$$ $$\sum_{n=0}^{n} n = \frac{n * (n + 1)}{2}$$

WARNING: If the sum goes from 0 to n, there are n + 1 terms!
For instancec, from 0 to 4, there is 0, 1, 2, 3, 4, which is 5 terms.

Let Sn be the sum of all the terms of an arithmetic sequence between rank p and rank n (p

Boom! You have seen everything there is to do with arithmetic sequences. We have taken a tour of all its formulas, but above all you don't have to know them by heart since we know how to find them all (it's still easier when you're struggling, nope?). Next step: geometric sequences.
(Back To Top)