Les suites arithmétiques sont un bon point de départ pour comprendre les autres types de suites. Je vous invite cependant à lire rapidement le cours d’introduction sur les suite et celui concernant le sens de variation d'une suite si ce n’est pas déjà fait ;)

Ce sera beaucoup plus simple ici, une suite arithmétique est juste un cas particulier très facile à identifier. En voici sa definition:

\( U_{n} \) est une suite arithmétique s'il existe un nombre \( r \) tel que, pour tout \( n\in \mathbb{N} \): $$U_{n+1}=U_{n} + r$$ Le réel r s'appelle la raison de la suite arithmétique.

Ok, mais y’a moyen de le faire en plus clair?!

Avec une suite arithmétique, nous ajoutons toujours la même valeur (constante) entre deux termes consécutifs. C’est cette relation de récurrence qui définit toutes les suites arithmétiques.

Attention cependant, la valeur ajoutée r est constante mais peut être négative.

Commençons par identifier le cas dans lequel nous manipulons bien une suite arithmétique.

Si nous avons déjà lu le cours concernant le sens de variation d’une suite, nous pouvons nous rappeler que trouver la relation de récurrence entre deux termes revient à calculer la différence entre ces deux termes. De la même manière, nous allons calculer ici \( U_{n+1} - U_n \) et voir si cette différence est constante (si on ajoute toujours la même valeur). Autrement dit:

Si \( U_{n+1} - U_n = r \) où r est un réel (donc une constante), alors la suite est arithmétique de raison r.

En effet, écrit autrement, on retrouve notre définition: $$U_{n+1} = U_n + r$$

Inversement, si \( U_{n+1} - U_n \) n'est pas égal à une constante, nous pouvons conclure que la suite \( U_n \) n'est pas arithmétique.

Certains d'entre vous ont peut être déjà la représentation graphique en tête. Avec une suite arithmétique nous ajoutons toujours la même valeur, c'est exactement comme dans un escalier; avec r, le nombre de marches que l’on monte ou l’on descends à chaque pas.

Si nous calculons les trois premiers termes de notre suite \( U_n = -3n + 4 \):

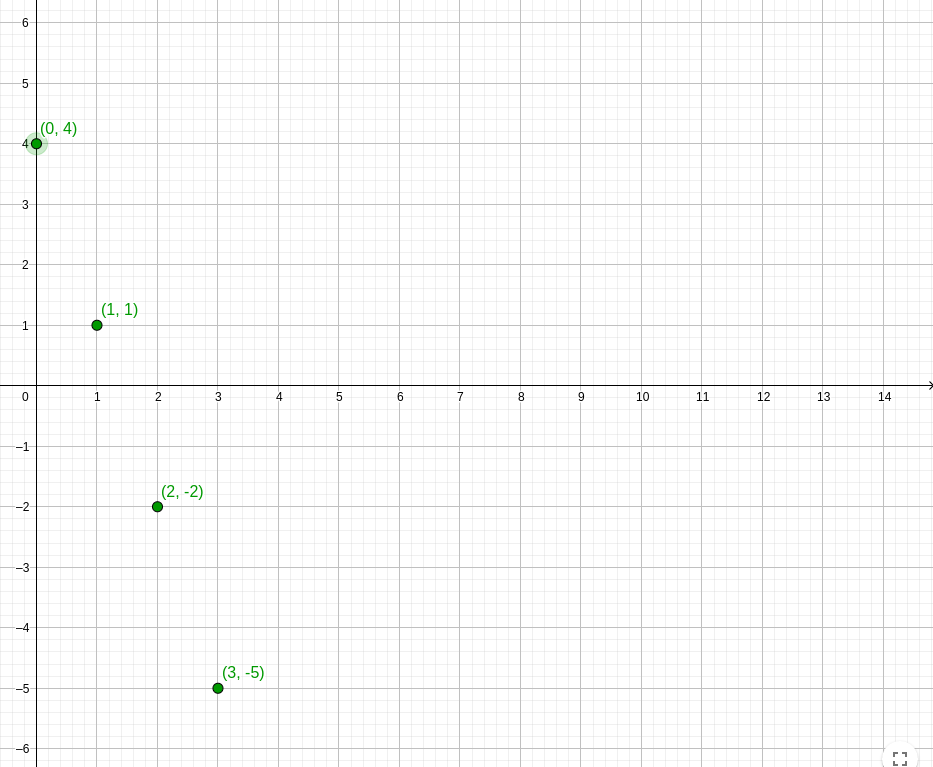
Nous descendons les marches trois par trois (paies ta cheville...).

Profitons en pour faire le parallèle avec les fonctions. On change \(n\) en \(x\), et \( U_n \) en \( f(x) \): $$ U_n = -3n + 4 $$ $$ f(x) = -3x + 4 $$

Esh, je connais ca; fonction affine ou linéaire délire du genre non?
Exact. Une suite arithmétique est une fonction affine définie uniquement pour certains points.

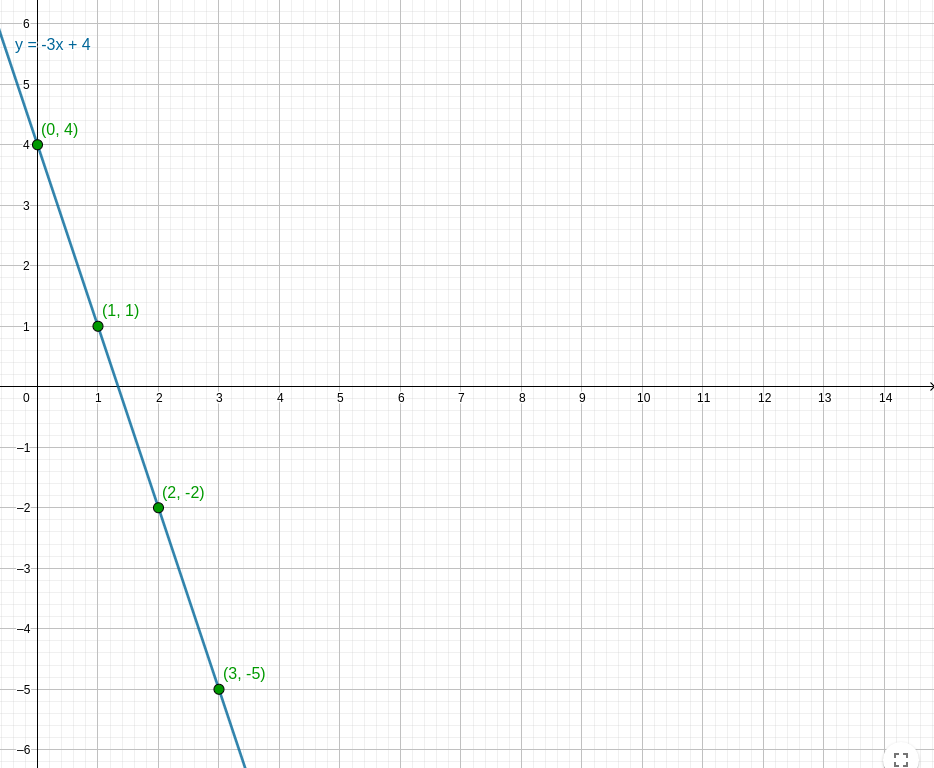
Nous voyons ici clairement le lien entre une suite arithmétique et une fonction affine: $$ f(x) = ax + b $$ $$ U_n = an + b $$ Nous retrouvons 'a' comme coefficient directeur et 'b' comme valeur initial (offset). La propriété suivante finira d'illuster ce lien ^^

Si a et b sont deux nombres réels et si la suite \(U_{n}\) est définie par: $$ U_{n}=a \times n+b $$ alors cette suite est une suite arithmétique de raison \( r = a \) et de premier terme \( U_{0} = b \).

A ce stade, ce chapitre ne mériterait presque pas d'exister :D
Rappelons tout de meme cette propriété:

Si \( U_{n+1} - U_n = r \) où r est un réel, alors la suite est arithmétique de raison r.

Le théoreme suivant devient alors évident (bon, il faut quand meme avoir lu le cours sur le sens de variation d'une suite):

Soit \(U_{n}\) une suite arithmétique de raison r :

si r > 0 alors \(U_{n}\) est strictement croissante.
si r < 0 alors \(U_{n}\) est strictement décroissante.
si r = 0 alors \(U_{n}\) est constante.

C'est tout?
Yup!

Cool! Nous allons maintenant finir ce cours avec deux choses super importantes:
- Deviner la relation \( U_n \) en fonction de n.
- Calculer la somme d'une suite arithmétique, genre:
1 + 2 + 3 + 4 + ... + 100 = ? (avouez qu'on a tous envie de savoir répondre a ca en 2 secondes ^^).

C'est parti pour cette derniere ligne droite.

Bon du coup les gars, comment on peut calculer \( U_{10} \) d'une suite arithmétique directement?

Easy gros, tu nous a dit qu'on ajoutait toujours la meme chose. Donc \( U_{10} \) c'est ce qu'on avait au début + 10 paies: \( U_{10} = U_0 + 10r \). Tu nous as meme deja lacher la formule avec \(U_n = b + an \).

Carrément... On se fait quand meme le raisonnement, c'est le genre de chose qui vous sera régulierement demandé et nous permet de trouver la forme explicite de nombreuses suites.

Nous allons considérer ne connaitre que la relation de récurrence : $$U_{n+1}=U_{n} + r$$ Et l'ídée ca va etre de trouver la forme explicite, donc \( U_n \) en fonction de n.

Apres toi...
C'est comme dans les jeux de logique "trouver la suite logique de cette série" ou "trouver le numéro manquant dans cette séquence". Comment ? Commencons par calculer les premiers termes \( U_0, U_1, U_2, U_3 \):

\(U_{0} \) (le terme initial donné)
\(U_{1} = U_{0} + r \) (Ok)

\(U_{2} = U_{1} + r \) (on remplace avec ce que vaut \(U_{1}\))
\( \quad = (U_{0} + r) + r\)
\( \quad = U_{0} + 2r\)

\(U_{3} = U_{2} + r \) (on remplace avec ce que vaut \(U_{2}\))
\( \quad = (U_{0} + 2r) + r\)
\( \quad = U_{0} + 3r\)
...

On voit clairement le pattern \( U_n = U_0 + nr \)
Ouep. Maintenant que nous avons ca, nous allons corser vite fait le truc et utiliser notre méga technique de manipulation des suites. Petit rappel:

Parfois les suites ne commencent pas à 0.
Par exemple on pourra définir une suite "Pour tout n ≥ 3". Dans ce cas \( U_{0} \), \( U_{1} \) et \( U_{2} \) n’existent pas; nous calculons les termes à partir de \( U_{3} \).

Du coup, que devient la forme explicite si nous ne partons plus de 0?
...

Cette fois-ci nous allons vouloir exprimer \( U_n \) en fonction d'un autre terme qui n'est pas \( U_0 \), disons \( U_p \) - (j'ai choisi p pour 'premier').

Tu n'arrêtes pas de nous dire que calculer la différence entre deux termes, c'est définir leur relation. On fait ca non?
Bingo.

$$ U_n = U_0 + n \times r $$ $$ U_p = U_0 + p \times r $$
$$ U_n - U_p = (U_0 + nr) - (U_0 + pr) $$ $$ \quad = U_0 + n \times r - U_0 - p \times r $$ $$ \quad = (n - p) \times r $$
Nous venons de trouver la forme explicite générale de toutes les suites arithmétiques!
Nous pouvons conclure:

Si la suite \(U_{n}\) est arithmétique de raison r alors pour tous entiers naturels n et p:
$$ U_n = U_p + (n - p) \times r $$

Aller dernière section, on va enfin calculer 0 + 1 + 2 + 3 + ...

Dernière technique de ouf de ce cours. Pour calculer la somme "S = 0 + 1 + 2 + 3 + ... + n", nous allons l'écrire une a l'endroit et une fois a l'envers:

\( (a) \quad S = \color{darkred}{0} + \color{goldenrod}{1} + \color{darkgreen}{2} + \cdots + \color{darkblue}{n} \)
\( (b) \quad S = \color{darkred}{n} + \color{goldenrod}{n - 1} + \color{darkgreen}{n - 2} + \cdots + \color{darkblue}{n - n} \)

Maintenant on additionne (a) + (b):

\( (a + b) \quad 2S = \color{darkred}{n} + \color{goldenrod}{n} + \color{darkgreen}{n} + \cdots + \color{darkblue}{n} \)

ATTENTION: Si la somme va de 0 à n, il y a n + 1 termes!
Par exemple, de 0 à 4, il y a 0, 1, 2, 3, 4, ce qui fait 5 termes.

Ainsi:
\( 2S = n * (n + 1) \)

Et pour conclure:
$$ S = \frac{n * (n + 1)}{2} $$

THÉORÈME (SOMME DES PREMIERS ENTIERS)
Pour tout entier \(n \in \mathbb{N} \): $$ 0 + 1 + 2 + \cdots + n = \frac{n * (n + 1)}{2} $$

Alors combien vaut \( 0 + 1 + 2 + \cdots + 100 \)?
\( S_{100} = \frac{100 * 101}{2} = \frac{10100}{2} = 5050 \)

Bad Ass Style

Tu vas découvrir la notation que tu retrouveras partout en mathématique, la somme: \( \sum_{n=0}^{n} \). Ca semble hyper compliqué, mais en fait ce n'est rien d'autre que Sn! Ce qu'il y a en dessous, c'est ou on commence et au dessus ou l'on fini. On peut ainsi réecrire notre théoreme:

THÉORÈME (SOMME DES PREMIERS ENTIERS)
Pour tout entier \(n \in \mathbb{N} \): $$ \sum_{n=0}^{n} n = \frac{n * (n + 1)}{2} $$

Formule Générale

Tu vas quand meme nous donner la formule qui marche pour toutes les suites arithmétiques?

Soit Sn, la somme de tous les termes d'une suite arithmétique compris entre le rang p et le rang n (p < n): $$ Sn = (n − p + 1) ∗ \frac{U_p + U_n}{2} $$

Voici un moyen visuel de se rappeler cette formule (la somme c'est comme la surface).

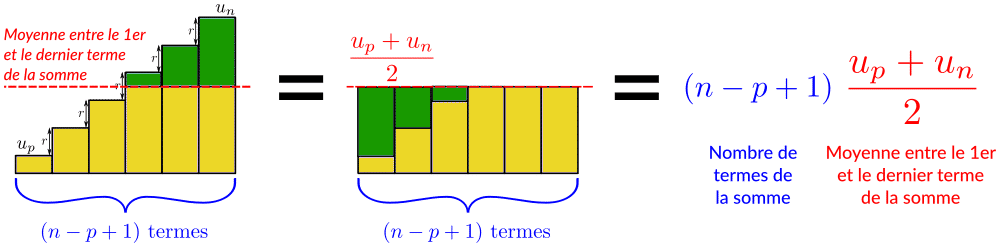
Pour les plus motivés, je vous propose d'en faire soi-meme la demonstration pour 'masteriser' ce cours.

\( U_{n} \) est une suite arithmétique s'il existe un nombre \( r \) tel que, pour tout \( n\in \mathbb{N} \): $$U_{n+1}=U_{n} + r$$ Le réel r s'appelle la raison de la suite arithmétique.

Si \( U_{n+1} - U_n = r \) où r est un réel (donc une constante), alors la suite est arithmétique de raison r.

Inversement, si \( U_{n+1} - U_n \) n'est pas égal à une constante, nous pouvons conclure que la suite \( U_n \) n'est pas arithmétique.

Si a et b sont deux nombres réels et si la suite \(U_{n}\) est définie par: $$ U_{n}=a \times n+b $$ alors cette suite est une suite arithmétique de raison \( r = a \) et de premier terme \( U_{0} = b \).

Soit \(U_{n}\) une suite arithmétique de raison r :

si r > 0 alors \(U_{n}\) est strictement croissante.
si r < 0 alors \(U_{n}\) est strictement décroissante.
si r = 0 alors \(U_{n}\) est constante.

Parfois les suites ne commencent pas à 0.
Par exemple on pourra définir une suite "Pour tout n ≥ 3". Dans ce cas \( U_{0} \), \( U_{1} \) et \( U_{2} \) n’existent pas; nous calculons les termes à partir de \( U_{3} \).

Si la suite \(U_{n}\) est arithmétique de raison r alors pour tous entiers naturels n et p:
$$ U_n = U_p + (n - p) \times r $$

THÉORÈME (SOMME DES PREMIERS ENTIERS)
Pour tout entier \(n \in \mathbb{N} \): $$ 0 + 1 + 2 + \cdots + n = \frac{n * (n + 1)}{2} $$ $$ \sum_{n=0}^{n} n = \frac{n * (n + 1)}{2} $$

ATTENTION: Si la somme va de 0 à n, il y a n + 1 termes!
Par exemple, de 0 à 4, il y a 0, 1, 2, 3, 4, ce qui fait 5 termes.

Soit Sn, la somme de tous les termes d'une suite arithmétique compris entre le rang p et le rang n (p < n): $$ Sn = (n − p + 1) ∗ \frac{U_p + U_n}{2} $$

Boom ! Vous avez vu tout ce qu'il y avait a avoir avec les suites arithmétiques. Nous avons fait le tour de toutes ses formules, mais surtout vous n'en avez aucune a apprendre puisqu'on sait comment toutes les retrouver (c'est quand meme plus simple quand on est galere, nope?). Next step: les suite géométriques.
(Remonter au début)