Accès Rapide
Introduction
Les suites posent beaucoup plus de problèmes aux lycéens que les fonctions... et pourtant l’idée est la même. Dans ce premier article, il y a l'essentiel des concepts pour comprendre l’étude des suites. Les suites arithmétiques et les suites géométriques seront ensuite facilement appréhendables.
Alors, une suite qu’est-ce-que c’est ?
En bref, c’est comme une fonction mais qui ne serait définie que pour des nombres entiers positifs. C’est-à-dire qu’il n’y aurait que des \(f(0), f(1), f(2), f(3)\)… et nous avons choisi de les écrire \(U_{0}, U_{1}, U_{2}, U_{3}\)…
Prenons par exemple une suite définie par \(U_{n} = 2n + 1\).
Avec une fonction nous aurions écrit \(f(x) = 2x + 1\).
Pour calculer les termes, il suffit donc juste de remplacer n par sa valeur
dans l’équation comme pour une fonction classique:
$$U_{0} = 2 * 0 + 1 = 1$$ $$U_{1} = 2 * 1 + 1 = 3$$ $$U_{2} = 2 * 2 + 1 = 5$$ $$U_{3} = 2 * 3 + 1 = 7$$ $$...$$
Intuitivement, une suite peut aussi être considérée comme une simple liste ordonnée de nombres. La suite précédente pourrait se définir avec la liste { 1, 3, 5, 7, ... }.
Voilà ce qu'est une suite, rien d'autre. C’est vraiment aussi simple; tout le reste n'est qu'une écriture mathématique pour en faciliter la manipulation.
Note:
n est toujours positif !
Parfois les suites ne commencent pas à 0.
Par exemple on pourra définir une suite "Pour tout n ≥ 3".
Dans ce cas \( U_{0} \), \( U_{1} \) et \( U_{2} \) n’existent pas;
nous calculons les termes à partir de \( U_{3} \).
Quelques exemples d'utilisations
- Savoir combien d’argent nous pouvons économiser avec une paie régulière (suite arithmétique).
- Les prêts bancaires sont modélisés avec des suites géométriques; les comprendre vous évitera de vous faire avoir par votre banquier ;)
- Prédire l'évolution d'une épidémie au sein d'une population.
- Comprendre les nombres premiers et leur répartition pour faire de la crypto, du hacking ou simplement des maths ^^.
- Prédire l'évolution des populations des animaux ou des humains. Par exemple, le nombre de lapins total que peut générer un seul couple de lapins en quelques mois (suite de Fibonacci).
- Trouver la valeur approchée de certaines fonctions (indispensable pour le numérique) ou de nombres comme π.
Représentation Graphique
La représentation graphique d'une suite \(U\) est l'ensemble des points de coordonnées \( \{ n; U_{n} \} \) où n décrit les entiers naturels pour lesquels \(U_{n}\) est défini.
Nous procédons comme pour les fonctions { x, y = f(x) }; à la seul différence que la suite est représentée par des points, puisque la suite n’est définie que pour 0, 1, 2, 3…
Exemple
Reprenons notre suite définie par \(U_{n} = 2n + 1\).
Nous mettons les termes précédemment calculés dans un tableau:
| n | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \( U_{n} \) | 1 | 3 | 5 | 7 | 9 |
Et on obtient la représentation graphique des premiers points de la suite :
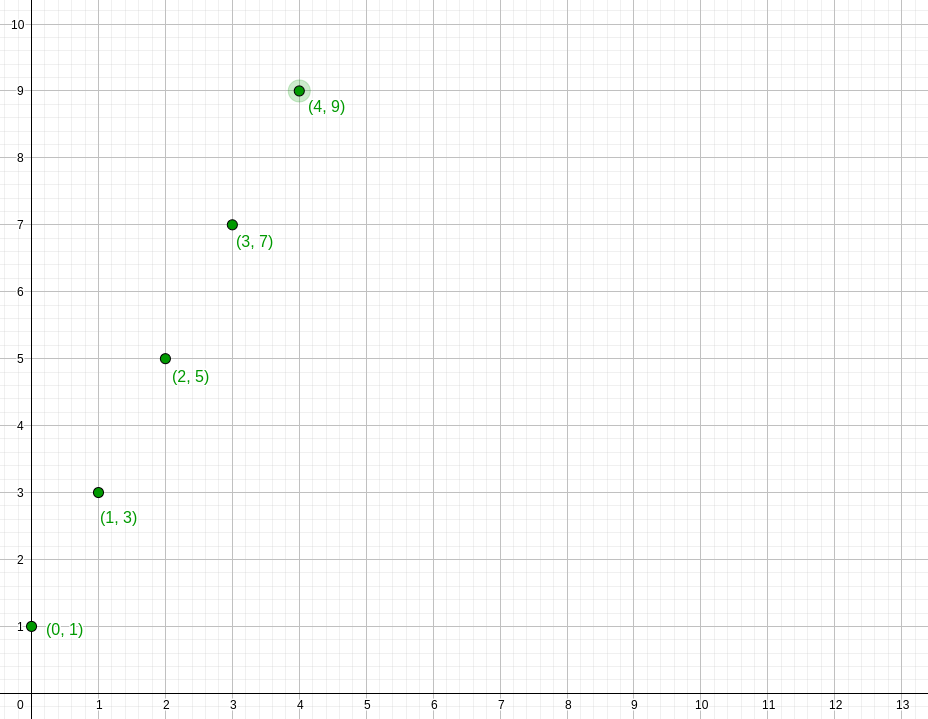
Définir une suite
Définitions
Une suite \(U\) associe à tout entier naturel \(n\) un nombre réel noté \(U_{n}\).
Les nombres réels \(U_{n}\) sont les termes de la suite.
Les nombres entiers \(n\) associés sont les indices ou les rangs.
La suite \(U\) peut également se noter \(U_{n}\) ou \(U_{n_{n \in \mathbb{N}}}\)
Ensuite il faut savoir qu’il y a 2 façons de décrire une suite. Il est important de comprendre les deux car nous aurons souvent à les manipuler ou devoir passer de l’une à l’autre.
La forme explicite ou générale
La forme explicite est comme celle d’une fonction habituelle, elle nous donne \(U_{n}\) en fonction de \(n\):
$$U_{n} = f(n)$$ où f est une fonction définie dans \(\mathbb{N}\)
Celle-ci permet de calculer n’importe quel termes de la suite directement, sans connaitre le terme précédent (on remplace simplement n dans la formule). Nous aurons souvent à retrouver cette forme depuis celle de récurrence.
Exemple
Notre suite qui nous suit depuis le début est définie par \(U_{n} = 2n + 1\).
C'est la forme explicite et si nous voulons calculer \(U_{30}\):
$$ U_{30} = 2*30 + 1 = 61$$
La forme par récurrence
Si nous revenons un petit peu sur le graphique et les premiers termes de notre suite, on se rend compte qu’il nous suffit d’ajouter 2 à chaque fois pour passer d’un point à un autre. Pour rappel:
$$U_{0} = 1$$ $$U_{1} = 3$$ $$U_{2} = 5$$ $$U_{3} = 7$$ $$...$$
Pour exprimer cette relation entre un terme et son suivant mathématiquement, il suffit d'écrire le terme initiale et la formule qui lie deux termes consécutifs.
Exemple
Toujours avec notre suite { 1, 3, 5, 7, ... }:
$$U_{0} = 1$$
$$U_{n+1} = U_{n} + 2$$
Avec cette notations, on voit facilement la relation entre un état (terme) et le suivant: c'est ce qu'on appelle la relation de récurrence (comme en informatique) et la plupart des suites sont définies de cette manière.
Note:
Pour calculer \(U_{4}\), nous utilisons "n = 3" car "n + 1" doit valoir 4.
$$U_{4} = U_{3+1} = U_{3} + 2 = 9$$
Mais, comment on calcul \(U_{30}\) avec cette forme?
On remplace simplement dans la formule:
\(U_{30} = U_{29} + 2\) (...mais on a besoin de \(U_{29}\)!)
\(U_{29} = U_{28} + 2\) (...mais on a besoin de \(U_{28}\)!)
\(U_{28} = U_{27} + 2\) (...mais on a besoin de \(U_{27}\)!)
...
\(U_{1} = U_{0} + 2\) Ah!
Euh... c'est pas trop pratique...
Pour cette opération précise, c'est vrai que c'est pas pratique et le challenge sera souvent de retrouver la formule générale à partir de notre relation de récurrence.
C'est le plus souvent ce qui est fait quand on modelise un phénomène (e.g. météo):
- A partir de mesures ponctuelles, nous cherchons ce qui change entre deux états (récurrence).
- Puis on en déduit un modèle qui décrit plus généralement son évolution (explicite).
Mais cette forme restera aussi extrêmement utile pour bien des choses que nous verrons par la suite ;)
Le piège à éviter
Faire la différence entre l'indice n et la valeur de n dans la formule!
C'est l'erreur la plus commise (et de loin en tête).
La distinction indice/valeur c'est vraiment le truc le plus important pour ne pas se perdre.
Quand n est utilisé comme indice,
il est toujours "collé" à la lettre qui représente la suite.
Par exemple lorsque l'on écrit \(U_{n}\) ou encore \(U_{n+1}\).
Et dans ce cas, on ne peut pas le bouger : il représente le rang du terme de la suite.
Dans tous les autres cas il est utilisé comme valeur.
C'est alors exactement comme le x que nous avons l'habitude de manipuler dans les équations.
Exemple
Prenons une suite définie par la relation de récurrence:
$$\color{blue}{U_{n+1}} = \color{green}{n} * \color{blue}{U_{n}} + 2\color{green}{n}$$
Pour \(\color{blue}{U_{n+1}}\) et \(\color{blue}{U_{n}}\), n est l'indice.
Sinon n est une valeur.
Ici, nous pouvons réécrire l'équation comme suit: $$ \color{blue}{U_{n+1}} = \color{green}{n} * ( \color{blue}{U_{n}} + 2) $$
Fiche récapitulative
Les nombres réels \(U_{n}\) sont les termes de la suite.
Les nombres entiers \(n\) associés sont les indices ou les rangs.
Formule explicite: comme celle d’une fonction habituelle. $$U_{n} = f(n)$$ où f est une fonction définie dans \(\mathbb{N}\)
Fomule de récurrence: le terme initiale et la formule qui lie deux termes consécutifs. $$U_{0} = C^{ste}$$ $$U_{n+1} = f(U_{n})$$
Faire la différence entre l'indice n et la valeur de n dans la formule!
Pour calculer \(U_{n}\), nous utilisons l'indice de valeur (n - 1).
$$U_{4} = U_{3 + 1}$$
Et voila ! Nous avons maintenant tout ce qu’il nous faut pour comprendre les cas plus pratiques comme les suites arithmétique et les suites géométriques. Nous pouvons aussi voir les notions plus générales comme le sens de variation, la convergence et les limites.
(Remonter au début)

 Sens de variation - Monotonie
Sens de variation - Monotonie
 Suites Arithmétiques
Suites Arithmétiques