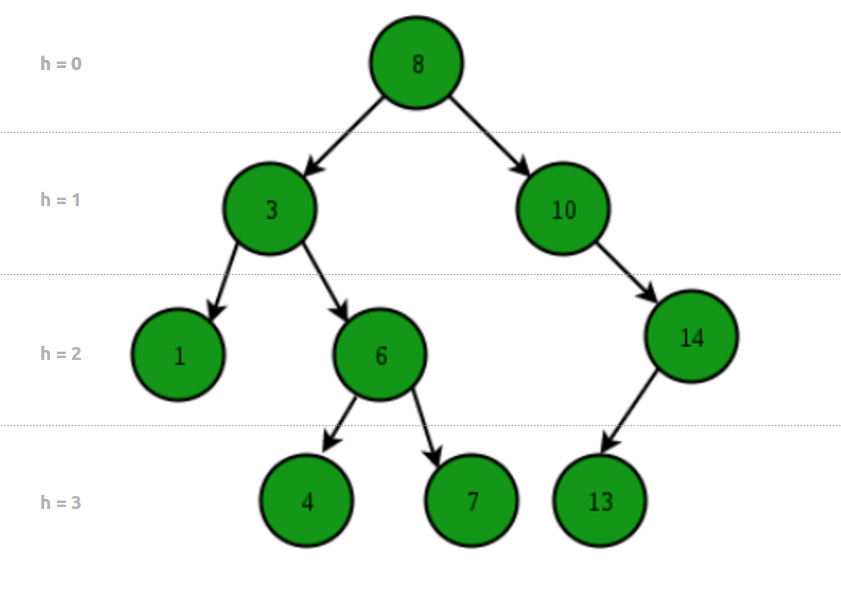
Un arbre binaire de recherche (ABR), ou Binary Search Tree (BST) en anglais, est un arbre ordonné. C'est la première structure de données arborescente que nous étudierons. Contrairement aux tableaux (array), aux listes liées (linked list), aux piles (stack) et aux files d'attente (queue) qui sont des structures de données linéaires, un arbre est une structure de données hiérarchique (non linéaire) intrinsèquement récursive. Pourtant, un BST est facile à comprendre et à manipuler. Voici à quoi ça ressemble:

L'une des raisons d'utiliser les arbres peut être parce que nous voulons stocker des informations qui forme naturellement une hiérarchie. Une autre très importante est leur caractéristique permettant des opérations d'insertion, de recherche et de suppression rapides - O(log n).

Tree, Binary Trees and Binary Search Trees (BST)

Avant de s'attaquer au BST, il est important de préciser les terminologies qui sont souvent confuses.

Tree - Arbre

Un arbre n'a aucune restriction sur le nombre d'enfants que chaque nœud peut avoir. Le nœud le plus haut d'une arborescence est appelé le nœud racine (root) et les nœuds sans enfants sont appelés feuilles (leafs). Ces arbres sont également appelés arbres N-ary (N-ary Tree):

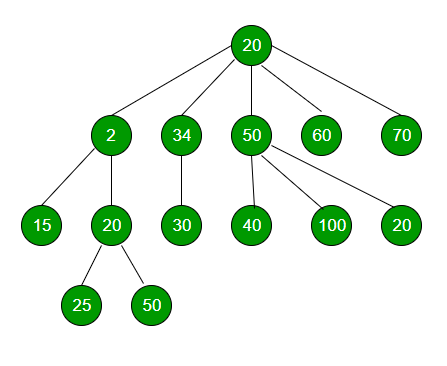
La hauteur d'un arbre est le nombre de liens entre la racine et la feuille la plus profonde (ici hauteur = 3).

Binary Tree - Arbre Binaire

Les arbres binaires sont un concept général d'une structure de données basée sur celle d'un arbre. Divers types d'arbres binaires (par exemple le BST étudié) peuvent être construits avec différentes propriétés basées sur ce concept. Les arbres binaires peuvent avoir au plus deux enfants pour chaque nœud. Chaque nœud dans un arbre binaire contient:
- Une donnée (e.g. 6)
- Un pointeur au nœud «enfant gauche» (peut être‘null’)
- Un pointeur au nœud «enfant droite (peut être ‘null’)

Cela peut sembler surprenant, mais l'organisation du code Morse est un arbre binaire.

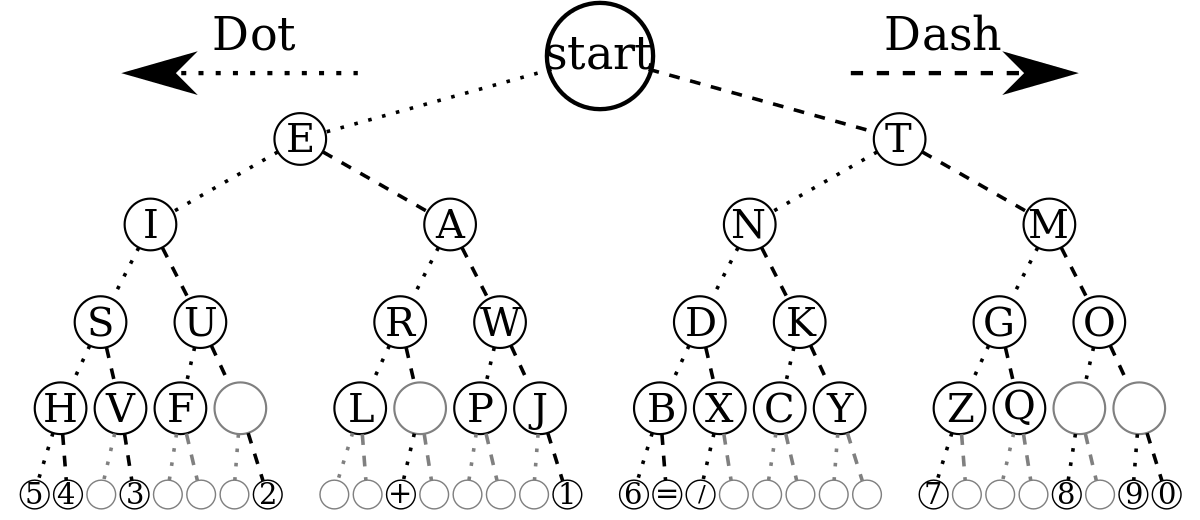
Quelques autres applications d'arbres binaires

• Permet de structurer des expressions mathématiques dans une calculatrice (arbre de syntaxe). C’est par exemple ce qui est utilisé par notre IA Globo pour résoudre pas à pas vos équations quadratiques.
• Construit par des compilateurs pour analyser les expressions (arbre de syntaxe)
• Utilisé dans presque tous les jeux vidéo 3D pour déterminer quels objets doivent être rendus (partition d'espace binaire).
• Utilisation dans des algorithmes de compression tels que mp3, jpg (Huffman Coding Tree)...

Binary Search Tree (BST) - Arbre Binaire de Recherche (ABR)

Vient enfin notre BST, qui est une structure de données d'arbre binaire avec les deux contraintes suivantes:
- Tous les nœuds du sous-arbre gauche d'un nœud ont une valeur inférieure ou égale à la valeur du nœud.
- Tous les nœuds du sous-arbre droit d'un nœud ont une valeur supérieur à la valeur du nœud.

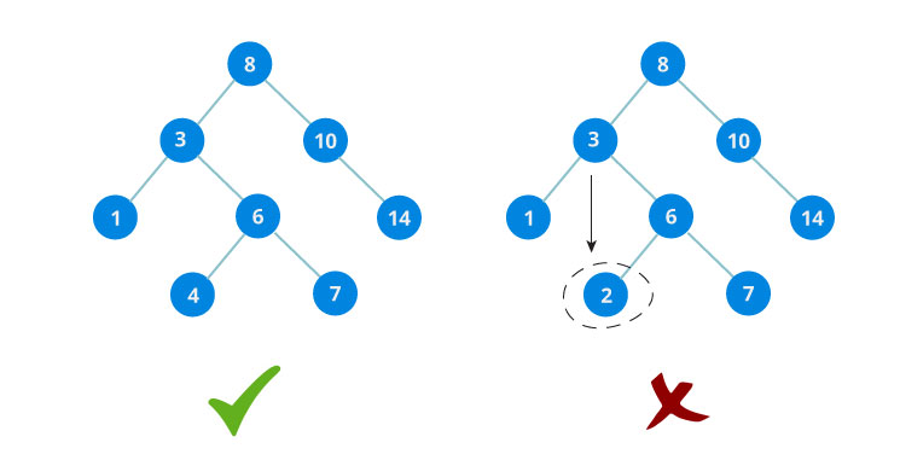
L'arbre binaire de droite n'est pas un arbre de recherche binaire car le sous-arbre droit du nœud "3" contient une valeur plus petite que celle-ci.

Faisons une pause avec quelques fractales d'arbres binaires

Manipuler un BST.
Construire notre propre structure de BST.
Mettre en pratique les pointeurs et la récursivité.
Comprendre les avantages / inconvénients de l'équilibrage d'un arbre.

Et ensuite?

Nous pouvons aller aux algorithmes de génération de labyrinthe. Jouer avec et utiliser notre explorateur nous donnera un aperçu visuel de la dualité entre un labyrinthe et une structure arborescente. Nous étudierons bientôt des structures arborescentes plus avancées telles que l'arbre rouge-noir (red-black tree) ou, les quadtrees et les octrees qui sont deux structures très utiles pour partitionner des espaces 2D et 3D.

Nous allons d'abord définir simplement notre structure d'arbre binaire contiennant: une donnée, un pointeur vers le sous-arbre gauche (nœud), un pointeur vers le sous-arbre droit (nœud). Le code est simplifié pour la lecture, veuillez utiliser le lien github pour accéder à la version complète.

  class BST
  {
    BST(const Value data) : data(data) {}
    ...

  private:
    T data;
    unique_ptr< BST > leftChild;
    unique_ptr< BST > rightChild;
  }

La sémantique du code montre que la récursivité joue un rôle majeur dans les structures de données arborescentes. En effet, les nœuds gauche et droit d'un BST sont des sous-arbres également définis comme BST.

Les arborescences de recherche binaire prennent en charge tout ce que nous pouvons obtenir à partir d'un tableau trié: recherche efficace, traversée avant / arrière dans l'ordre à partir d'un élément donné, recherche de prédécesseurs / successeurs et requêtes min / max ...

Pourquoi ne pas utiliser un simple tableau trié et utiliser alors la recherche binaire?

Avoir un tableau trié est utile pour de nombreuses tâches car il permet d'effectuer une recherche Binaire (ou dichotomique) pour localiser efficacement les éléments: O (log n). Le problème avec un tableau trié est que les éléments ne peuvent pas être insérés et supprimés efficacement par rapport aux arbres de recherche binaires.

Parfait. Puisque nous avons de bonnes raisons de continuer, définissons notre API.

  // Manipulation
  void Insert(Value data)     // Insert an element
  BST* Remove(Value data)     // Remove an element - Return root or null if empty

  // Traversal
  Value GetMin()              // Return the minima
  Value GetMax()              // Return the maxima
  List< Value > InOrder()     // Proceed in order traversal (sorted sequence)
  BST* Search(Value data)     // Find an element
 

C'est une assez grosse API, nous allons la prendre une section à la fois pour maîtriser les opérations d'arborescence. Nous aborderons en premier les méthodes de parcours, puis, les méthodes de manipulation.

Parcours

GetMin / GetMax

Ce sont les méthodes les plus simples et elles nous permettent de nous souvenir des propriétés d'un BST:
- Tous les nœuds du sous-arbre gauche d'un nœud ont une valeur inférieure ou égale à la valeur du nœud.
- Tous les nœuds du sous-arbre droit d'un nœud ont une valeur supérieur à la valeur du nœud.

  // GetMin is getting the left most child
  const BST* GetMin()
  {
    auto curNode = this;
    while (curNode->leftChild)
      curNode = curNode->leftChild;

    return curNode;
  }

  // GetMax is getting the right most child
  const BST* GetMax()
  {
    auto curNode = this;
    while (curNode->rightChild)
      curNode = curNode->rightChild;

    return curNode;
  }
 

Ci-dessous la version récursive (plus de consommation mémoire).

  const BST* GetMin() { return this->leftChild ? this->leftChild->GetMin() : this; }
  const BST* GetMax() { return this->rightChild ? this->rightChild->GetMax() : this; }
 

Search - Recherche

La recherche d'une valeur utilise le même principe que la recherche binaire dans un tableau trié. Si la valeur est inférieure au nœud actuel, on peut dire avec certitude qu'elle se trouve dans le sous-arbre gauche, sinon c'est dans celui de droite.

  const BST* Search(const Value data)
  {
    // Value found returns node
    if (this->data == data)
      return this;

    // Value is less than current node - Recurse in left subtree if exists
    if (data < this->data)
      return this->leftChild ? this->leftChild->Search(data) : nullptr;

    // Recurse in right subtree if exists
    return this->rightChild ? this->rightChild->Search(data) : nullptr;
  }
 

Inorder traversal - Traversée dans l'ordre

Dans une traversée en ordre (inorder), nous visitons d'abord l'enfant de gauche (y compris son sous-arbre récursivement), puis le nœud actuel et enfin l'enfant de droite (y compris son sous-arbre récursivement). Notons que la méthode de traversée dans l'ordre nous permet d'obtenir tous les nœuds par ordre croissant.

  static void Inorder(const BST* node, List< Value >& result)
  {
    if (!node) return; // end of a branch (no data)

    Inorder(node->leftChild)  // Recurse in left subtree
    result.push(node->data);  // Get data
    Inorder(node->rightChild) // Recurse in right subtree
  }
 

Manipulation

Insert - Insertion

L'insertion d'une valeur à la position correcte est similaire à la recherche car nous voulons conserver la règle selon laquelle le sous-arbre gauche contient des valeurs inférieures à la racine (root) et le sous-arbre droit des valeurs supérieures. Nous continuons à aller à droite ou à gauche en fonction jusqu'à ce que nous soyons une feuille. Ensuite, nous y mettons le nouveau nœud (ou BST).

  void Insert(const Value data)
  {
    // Data lower or equal then its parent's one - Insert in the left side
    if (data <= this->data)
    {
      // Child is a leaf
      if (!this->leftChild) this->leftChild = unique_ptr< BST >(new BST(data));
      // Child is a subtree - Recurse in the left side
      else this->leftChild->Insert(data);
    }

    // Data is greater than its parent's one - Insert in the right side
    else
    {
      // Child is a leaf
      if (!this->rightChild) this->rightChild = unique_ptr< BST >(new BST(data));
      // Child is a subtree - Recurse in the right side
      else this->rightChild->Insert(data);
    }
  }
 

Nous avons peut-être remarqué que l'ordre d'insertion peut changer la forme de notre BST. C'est l'inconvénient mentionné précédemment: notre arbre peut être très déséquilibré (ou dégénéré).

Gauche: nous insérons dans l'ordre [4,2,5,1,3,6] --> O(log n)
Droite: nous insérons dans l'ordre [1,2,3,4,5,6] --> O(n)

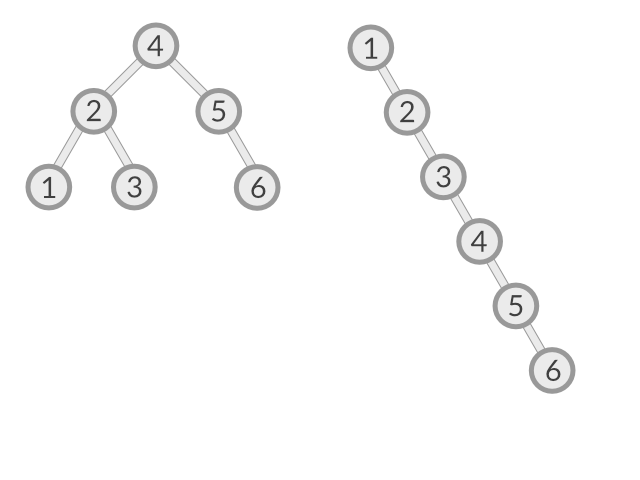
Nous pouvons voir que les temps d'exécution des algorithmes sur les arbres dépendent de leurs formes, qui, à leur tour, dépendent de l'ordre dans lequel les données sont insérées.

Il existe des techniques connues sous le nom d'équilibrage d'arbres permettant le maintient de l'équilibre des arbres. Nous les verrons avec des structures de données d'arbre plus avancées telles que les arbres rouge-noir (red-black trees).

Cependant, il est raisonnable pour de nombreuses applications d'utiliser un BST simple si nous supposons que les données sont insérées dans un ordre aléatoire. Dans ce cas, nos opérations avec n nœuds nécessitent environ 2 ln n.

Dans un premier exercice, nous pouvons écrire la procédure qui produira un BST équilibré à partir d'un tableau trié.

Remove / Suppression

La dernière opération dans le BST que nous allons discuter en profondeur est la suppression d'un nœud basé sur une valeur donnée. La suppression est un peu plus délicate que l'insertion car il y a trois cas à considérer si le nœud existe dans l'arborescence:

Le nœud est une feuille (pas d'enfant)

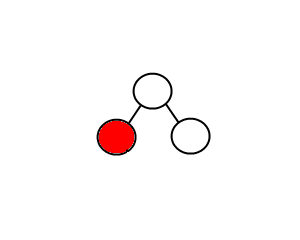
Dans ce cas, nous avons juste besoin de supprimer le nœud. What else?

Le nœud n'a qu'un seul enfant

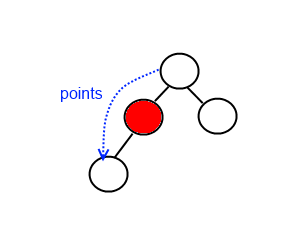
Si le nœud n'a qu'un seul enfant, la procédure de suppression est identique à la suppression d'un nœud d'une liste liée: nous contournons simplement le nœud en cours de suppression.

Le nœud a ses deux enfants

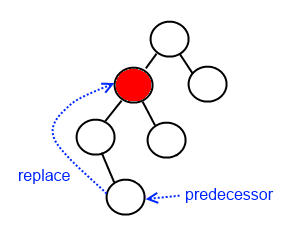
Dans ce cas, nous devons trouver le successeur (ou le prédécesseur) et le mettre à la place du nœud que nous supprimons.

Le prédécesseur est le nœud le plus grand (le plus à droite) du sous-arbre gauche.
Par symétrie, le successeur est le plus petit nœud (le plus à gauche) du sous-arbre droit.

  // To avoid useless code, let's suppose we found the node using the Search
  void Remove(BST* node)
  {
    // No child - Simply remove node
    if (!bst->leftChild && !bst->rightChild) bst.reset();

    // Left node is unique child - remove node and replace it with its child.
    else if (bst->leftChild) bst.reset(bst->leftChild.release());
    // Right node is unique child - remove node and replace it with its child.
    else if (bst->rightChild) bst.reset(bst->rightChild.release());

    // Both children:
    // - Swap node value with its predecessor
    // - Remove predecessor node
    else
    {
      auto& predecessor = bst->GetPredecessor();
      std::swap(bst->data, predecessor->data);
      predecessor.reset(predecessor->leftChild.release());
    }
  }
 

Voila! Nous maîtrisons désormais l'arbre binaire de recherche (BST) et ses opérations. Cela nous offre une base solide utilisée quotidiennement dans le développement de logiciels.

Quelques exercices

  bool IsBalanced()   // Check if the tree is balanced
  int MinHeight()     // Return the smallest branch height
  int MaxHeight()     // Return the highest branch height
  int Size()          // Return number of nodes composing the tree