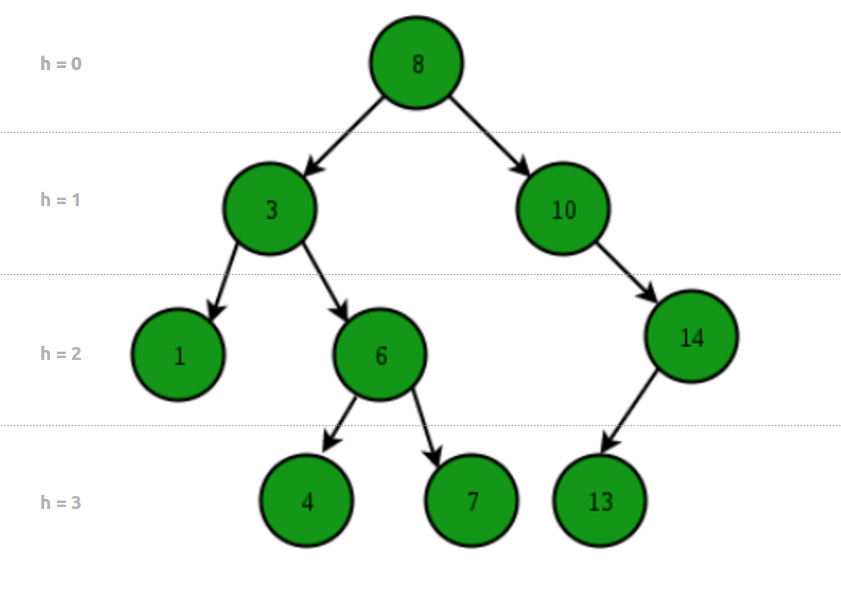
A Binary Search Tree (BST), Ordered Tree or Sorted Binary is the first tree data structure we are studying. Unlike Arrays, Linked Lists, Stacks and Queues which are linear data structures, a Tree is a hierarchical (and nonlinear) data structure which is intrinsically recursive. Still, BST are easy to understand and manipulate. Here is how it looks:

One reason to use trees might be because we want to store information that naturally forms a hierarchy. Another one is their very important characteristic that allows fast - O(log n) - insert, search and delete operations.

Tree, Binary Trees and Binary Search Trees (BST)

Before tackling BST it is important to precise the terminologies, which are often confused.

Tree

A tree has no restrictions on the number of children each node can have. The topmost node in a tree is called the root node and the nodes with no children are called leaf nodes. They are also called N-ary trees:

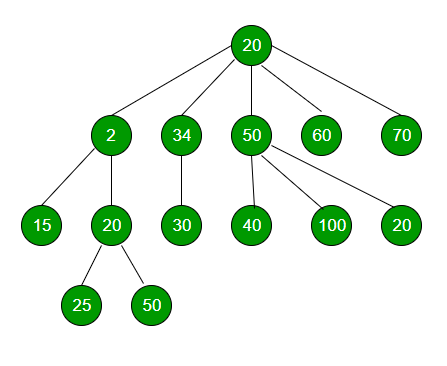
The height of a tree is the number of edges from the root to the deepest leaf (here height = 3).

Binary Tree

Binary trees is a general concept of particular tree-based data structure. Various specific types of binary trees (e.g. BST below) can be constructed with different properties based on this concept. Binary trees can have at most two children for each node. Every node in a binary tree contains:
- A data element (e.g. 6)
- A pointer to the 'left child' node (may be ‘null’)
- A pointer to the 'right child' node (may be ‘null’)

It may sound surprising, but the organization of the Morse code is a binary tree.

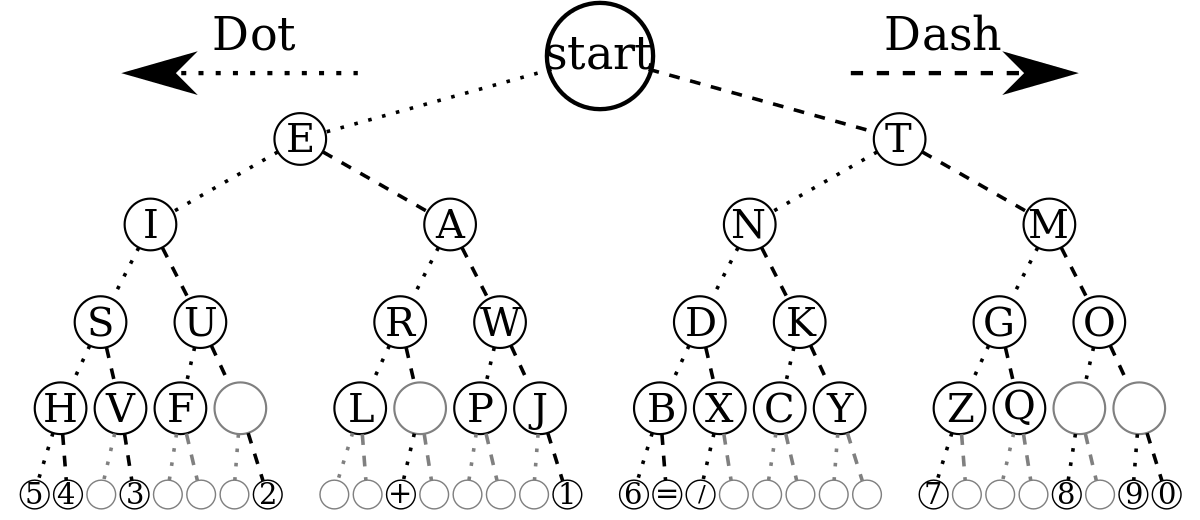
Some other applications of binary trees

• Use to structure mathematical expressions within a calculator (Syntax Tree). This is for instance what is used by our AI Globo to solve your quadratic equations step-by-step.
• Constructed by compilers to parse expressions as calculators (Syntax Tree)
• Used in almost every 3D video game to determine what objects need to be rendered (Binary Space Partition).
• Use in compression algorithms such as mp3, jpg (Huffman Coding Tree)...

Binary Search Tree - BST

Finally comes our BST, which is a binary tree data structure with the two following constraints:
- All nodes of the left subtree of a node have a value less than or equal to the node's value.
- All nodes of the right subtree of a node has a value greater to its parent's value.

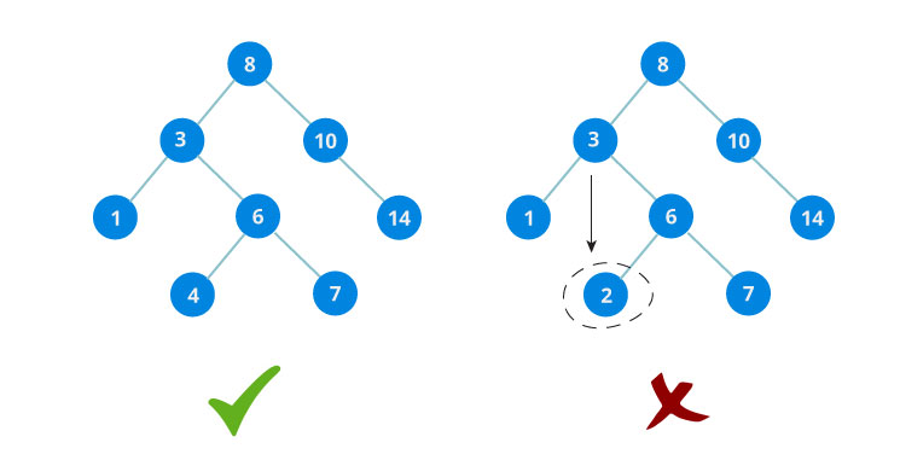
The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller than it.

Let’s have a break with some peaceful binary tree fractals

Operate a BST.
Build our own BST structures.
Put into practice pointers and recursion.
Understand the advantages / disadvantages of balancing a tree.

What is next?

If you haven't jumped yet to maze generation algorithms, playing with them and using our explorer gives you visual insights of the duality between a maze and a tree structure. We will soon study more advanced tree structures such as red-black tree or, quadtrees and octrees which are two very useful structures to partition 2D and 3D spaces.

We will first simply define our structure with Binary Trees that contains a data, a pointer to the left subtree (node), a pointer to the right subtree (node). The code is simplified for reading purpose, please use the github link to get access to the full version.

  class BST
  {
    BST(const Value data) : data(data) {}
    ...

  private:
    T data;
    unique_ptr< BST > leftChild;
    unique_ptr< BST > rightChild;
  }

The semantic of the code shows that recursion plays a major role in tree data structures. Indeed, the left and right nodes of a BST are subtrees also defined as BST.

Binary search trees support everything you can get from a sorted array: efficient search, in-order forward/backwards traversal from any given element, predecessor/successor element search, and max/min queries...

Why not using a simple sorted array and use binary search then?

Having a sorted array is useful for many tasks because it enables binary search to be used to efficiently locate elements : O(log n). The problem with a sorted array is that elements can't be inserted and removed efficiently in comparison with binary search trees.

Great. Since we have good reasons to proceed, let's define an API.

  // Manipulation
  void Insert(Value data)     // Insert an element
  BST* Remove(Value data)     // Remove an element - Return root or null if empty

  // Traversal
  Value GetMin()              // Return the minima
  Value GetMax()              // Return the maxima
  List< Value > InOrder()     // Proceed in order traversal (sorted sequence)
  BST* Search(Value data)     // Find an element
 

That’s a pretty big API, we will take it one section at a time to master tree operations. We will tackle them from the traversal methods to the manipulative ones.

Traversals

GetMin / GetMax

They are the easiest methods and they allow us to remember the properties of a BST:
- All nodes of the left subtree of a node have a value less than or equal to the node's value.
- All nodes of the right subtree of a node has a value greater to its parent's value.

  // GetMin is getting the left most child
  const BST* GetMin()
  {
    auto curNode = this;
    while (curNode->leftChild)
      curNode = curNode->leftChild;

    return curNode;
  }

  // GetMax is getting the right most child
  const BST* GetMax()
  {
    auto curNode = this;
    while (curNode->rightChild)
      curNode = curNode->rightChild;

    return curNode;
  }
 

See below the recursive version for illustration (more memory consumption).

  const BST* GetMin() { return this->leftChild ? this->leftChild->GetMin() : this; }
  const BST* GetMax() { return this->rightChild ? this->rightChild->GetMax() : this; }
 

Search

Searching for a value uses the same principle as the Binary Search in a sorted array. If the value is lesser than the current node, we can say for sure that the value is in the left subtree, otherwise it is in the right one.

  const BST* Search(const Value data)
  {
    // Value found returns node
    if (this->data == data)
      return this;

    // Value is less than current node - Recurse in left subtree if exists
    if (data < this->data)
      return this->leftChild ? this->leftChild->Search(data) : nullptr;

    // Recurse in right subtree if exists
    return this->rightChild ? this->rightChild->Search(data) : nullptr;
  }
 

Inorder traversal

In an inorder traversal, we first visit the left child (including its entire subtree), then visit the current node and finally visit the right child (including its entire subtree). Note that the binary search tree makes use of the inorder traversal method to get all nodes in ascending order of value.

  static void Inorder(const BST* node, List< Value >& result)
  {
    if (!node) return; // end of a branch (no data)

    Inorder(node->leftChild)  // Recurse in left subtree
    result.push(node->data);  // Get data
    Inorder(node->rightChild) // Recurse in right subtree
  }
 

Manipulate

Insert

Inserting a value in the correct position is similar to searching because we want to maintain the rule that left subtree is lesser than root and right subtree is larger than root. We keep going to either right or left depending on the value until we are a leaf. Then, we put the new node (or BST) there.

  void Insert(const Value data)
  {
    // Data lower or equal then its parent's one - Insert in the left side
    if (data <= this->data)
    {
      // Child is a leaf
      if (!this->leftChild) this->leftChild = unique_ptr< BST >(new BST(data));
      // Child is a subtree - Recurse in the left side
      else this->leftChild->Insert(data);
    }

    // Data is greater than its parent's one - Insert in the right side
    else
    {
      // Child is a leaf
      if (!this->rightChild) this->rightChild = unique_ptr< BST >(new BST(data));
      // Child is a subtree - Recurse in the right side
      else this->rightChild->Insert(data);
    }
  }
 

We may have noticed that the order of insertion may change the shape of our BST. This is the drawback mentioned earlier : our tree can be very unbalanced (or degenerate).

Left: we insert in order [4,2,5,1,3,6] --> O(log n)
Right: we insert in order [1,2,3,4,5,6] --> O(n)

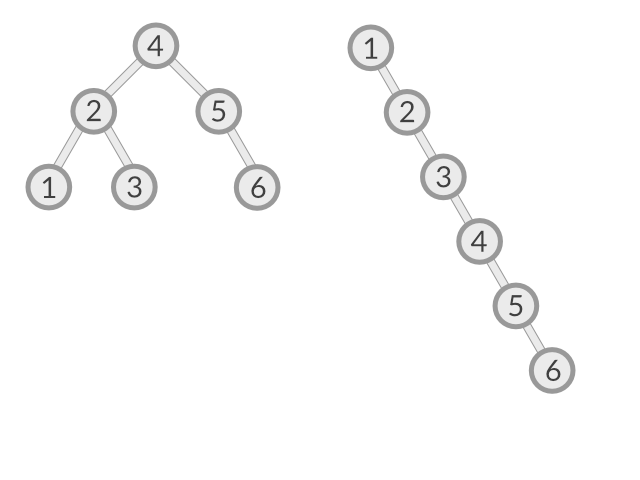
We can see that the running times of algorithms on binary search trees depend on the shapes of the trees, which, in turn, depends on the order in which keys are inserted.

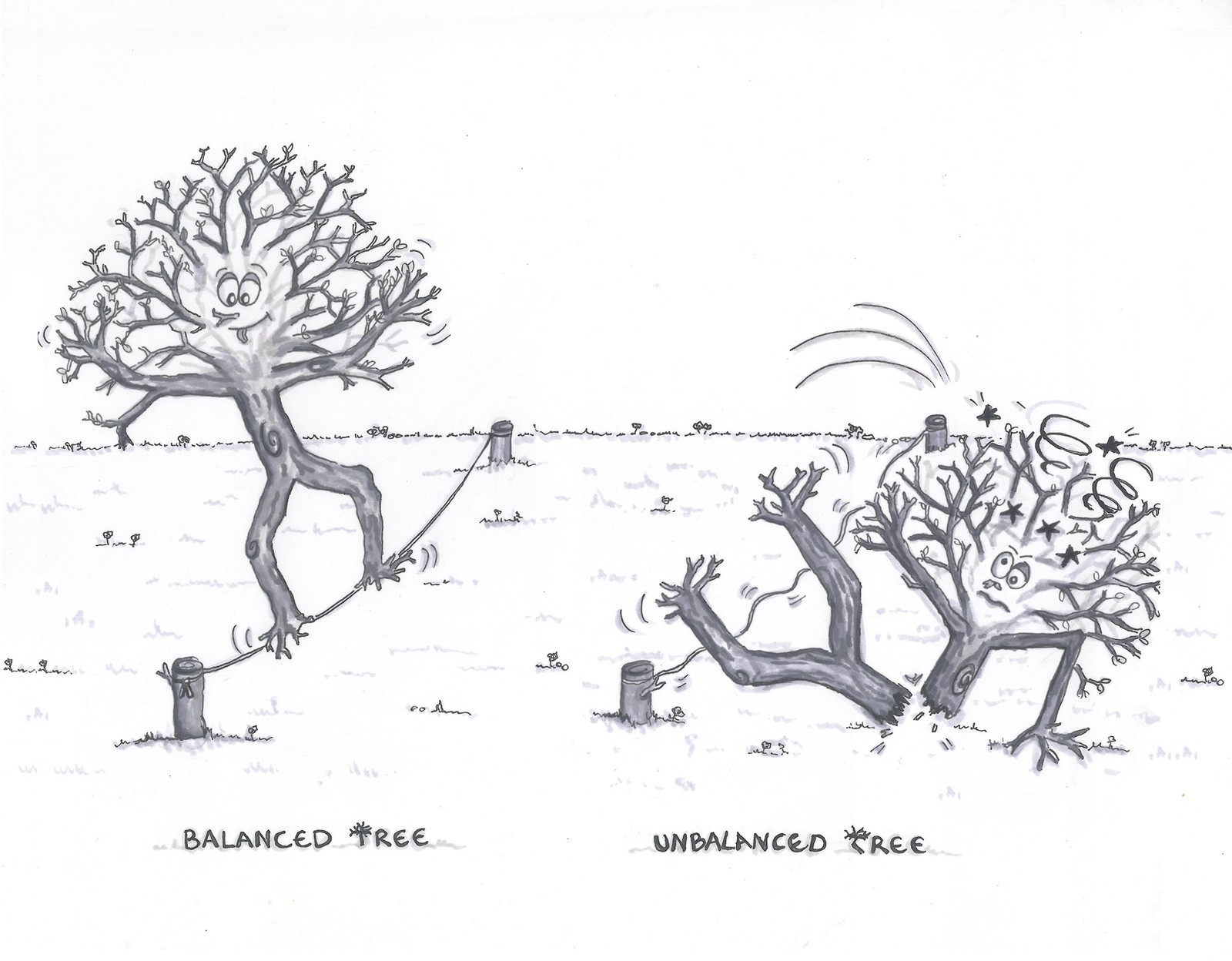
There are techniques known as tree balancing which maintain the tree balanced. We will see them with more advanced tree data structures such as red-black trees.

However, it is reasonable for many applications to use a BST if we assume that data are inserted in a random order. In that case, our operations with n nodes requires about 2 ln n.

As a first exercise we may write the procedure that will produce a balanced BST from a sorted array.

Remove

The last operation in the BST that we are going to discuss in depth is removing a node based on a given value. Deletion is somewhat more tricky than insertion as there are three cases to consider if the node exists in the tree:

Node is a leaf (no child)

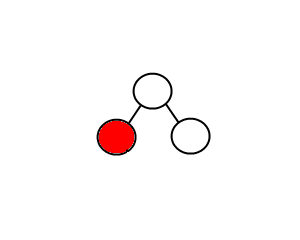
In this case, we just need to remove the node. What else?

Node has only one child

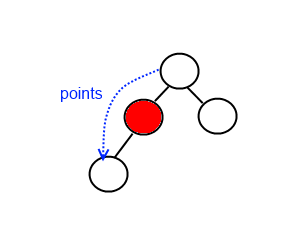
If the node has only one child the procedure of deletion is identical to deleting a node from a linked list - we just bypass that node being deleted.

Node has two children

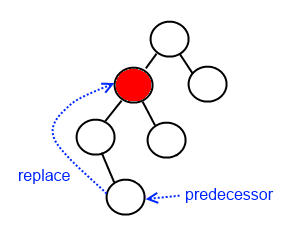
In this case, we have to find the successor (or predecessor) and put it where the node we throw away is.

The predecessor is the largest (right most) node in the left subtree.
By symmetry, the successor is the smallest (left most) node in the right subtree.

  // To avoid useless code, let's suppose we found the node using the Search
  void Remove(BST* node)
  {
    // No child - Simply remove node
    if (!bst->leftChild && !bst->rightChild) bst.reset();

    // Left node is unique child - remove node and replace it with its child.
    else if (bst->leftChild) bst.reset(bst->leftChild.release());
    // Right node is unique child - remove node and replace it with its child.
    else if (bst->rightChild) bst.reset(bst->rightChild.release());

    // Both children:
    // - Swap node value with its predecessor
    // - Remove predecessor node
    else
    {
      auto& predecessor = bst->GetPredecessor();
      std::swap(bst->data, predecessor->data);
      predecessor.reset(predecessor->leftChild.release());
    }
  }
 

Voila ! We now master BST and its operations, which give us a solid foundation daily used in software development.

Some exercises

  bool IsBalanced()   // Check if the tree is balanced
  int MinHeight()     // Return the smallest branch height
  int MaxHeight()     // Return the highest branch height
  int Size()          // Return number of nodes composing the tree