Dans le module résoudre une équation du 1er degré nous avons vu comment résoudre divers types d’équations linéaires; le genre d'équations qui apparaissent très naturellement dans la vie quotidienne.

Alors que les équations quadratiques, polynômes de degré deux ou de second ordre, ne sont pas si évidentes dans la vie quotidienne, elles sont toutes aussi importantes. Elles sont très souvent la solution dans la plupart des problèmes du monde réel : en physique, astronomie, ingénierie, informatique, architecture ... (voir ‘quelques cas courants’ ci-dessous).

Les équations de second ordre apparaissent aussi partout. Ce type d’équation était d'ailleurs déjà résolu à la fois par les Babyloniens et les Egyptiens à un stade très précoce de l'histoire (autour de 2000 ans avant notre ère). Les techniques de résolution ont ensuite été perfectionnées tout au long de l’histoire, dans le monde entier, avant d'être pleinement intégré aux mathématiques modernes (avec la formalisation des nombres complexes, mais vous n’en aurez pas besoin ici ^^).

Quelques cas courants

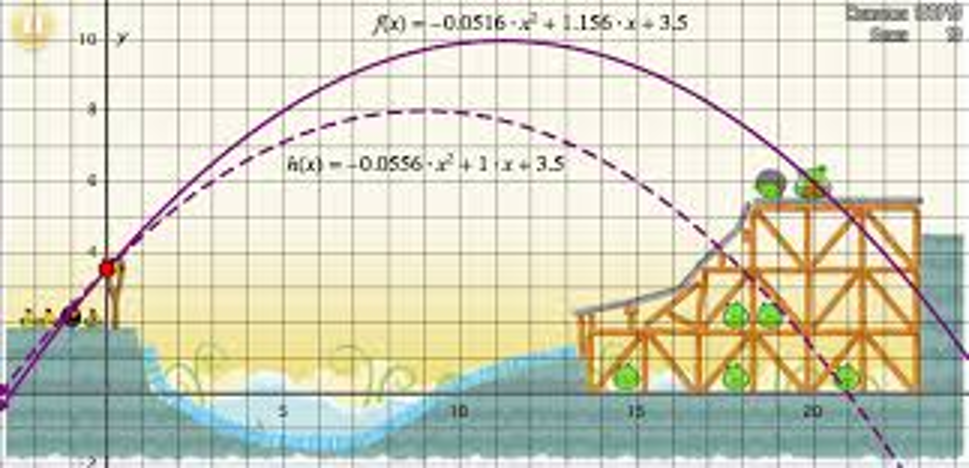
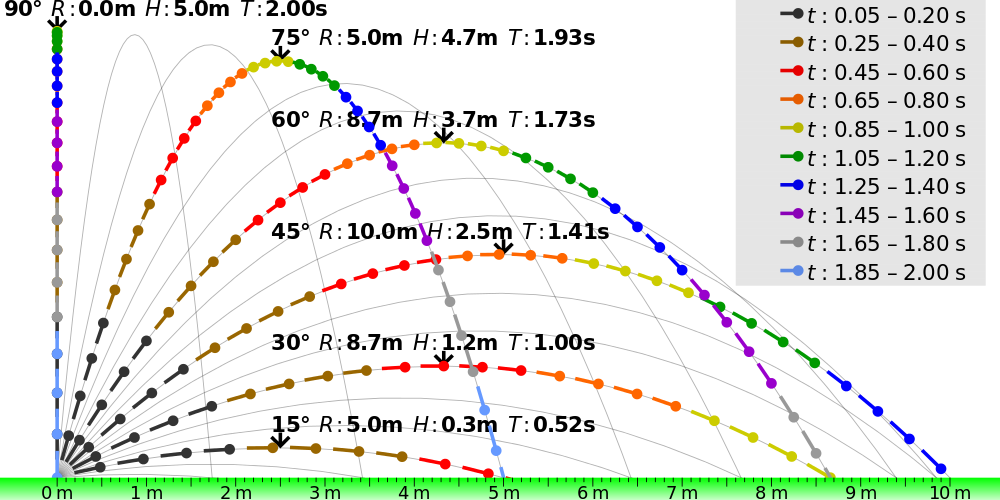
- Calculer toutes sortes de trajectoires (ballon, angry bird, saut d'une falaise, planètes…).
- Calculer toutes sortes d’optimisations telles que la maximisation des profits sur le marché.
- Calculer la puissance passant par un circuit électrique.
- Conceptualiser des télescopes, lentilles, miroirs et caméras.
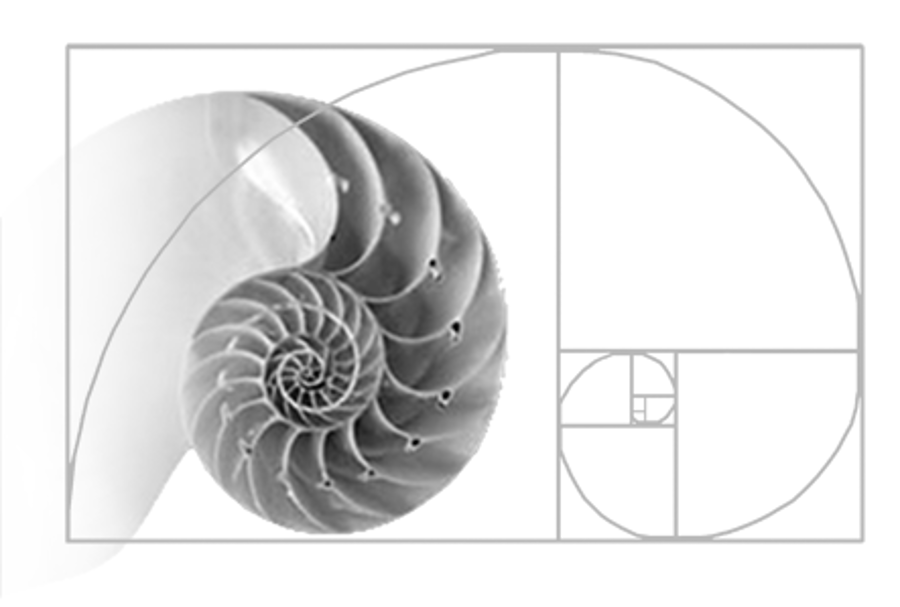
- Le nombre d’or est la solution positive de l’équation de second ordre x² - x - 1 = 0
(illustrations de Léonard de Vinci dans la Proportion Divine, la spirale d'or, la séquence de Fibonacci ...)
- Le percepteur d'impôt, une invention assez déplaisante de nos jours (réf. Babyloniens)...

Équations du 2nd degré placées sur la trajectoire du jeu Angry Bird (Gravité = Constante Gravitationnelle G).

Nombre d'or, spirales d'or, séquence de Fibonacci et la nature ensemble.
Le nombre d'or correspond à la solution positive de l'équation de second degré x² - x - 1 = 0.

Trajectoires de projectiles lancés à différents angles avec une vitesse de 10 m / s (source Wikipedia). On suppose la gravité uniforme G de 10 m / s².
t = temps au lancement
T = temps de vol,
R = longueure
H = point le plus haut (indiqué par les flèches).

Parabole de l'arc supérieur du pont de Sydney Harbour.

Une banane, 'just for scale'.

En pratique

En pratique, les équations du second ordre sont juste un pas de plus vis-à-vis des équations du premier ordre. Nous limitons toujours le problème à une seule inconnue x et ajoutons le terme x² (ou x * x). La forme générale de cette équation (après avoir tout déplacé du côté gauche) est la suivante: $$\textbf{ax² + bx + c = 0} ,\: \: où\: \: a \neq 0$$

Le Jeu

Les règles du jeu sont exactement les mêmes que pour les équations linéaires (cf. Règles du jeu des équations linéaires). Cependant, vous disposez maintenant de nouveaux outils et aussi d'une nouvelle méthodologie pour atteindre votre objectif. Petit à petit vous gagnez en puissance mathématique. Pour toujours résoudre une équation de second ordre deux possibilités (de la plus rapide à la plus générale) sont proposées ici. L’approche décrite est indispensable pour aborder facilement toutes les équations de second ordre.

Outils

Discriminant

Solution générale

Essayer tout d'abord de reconnaitre une forme canonique (Factorisation)

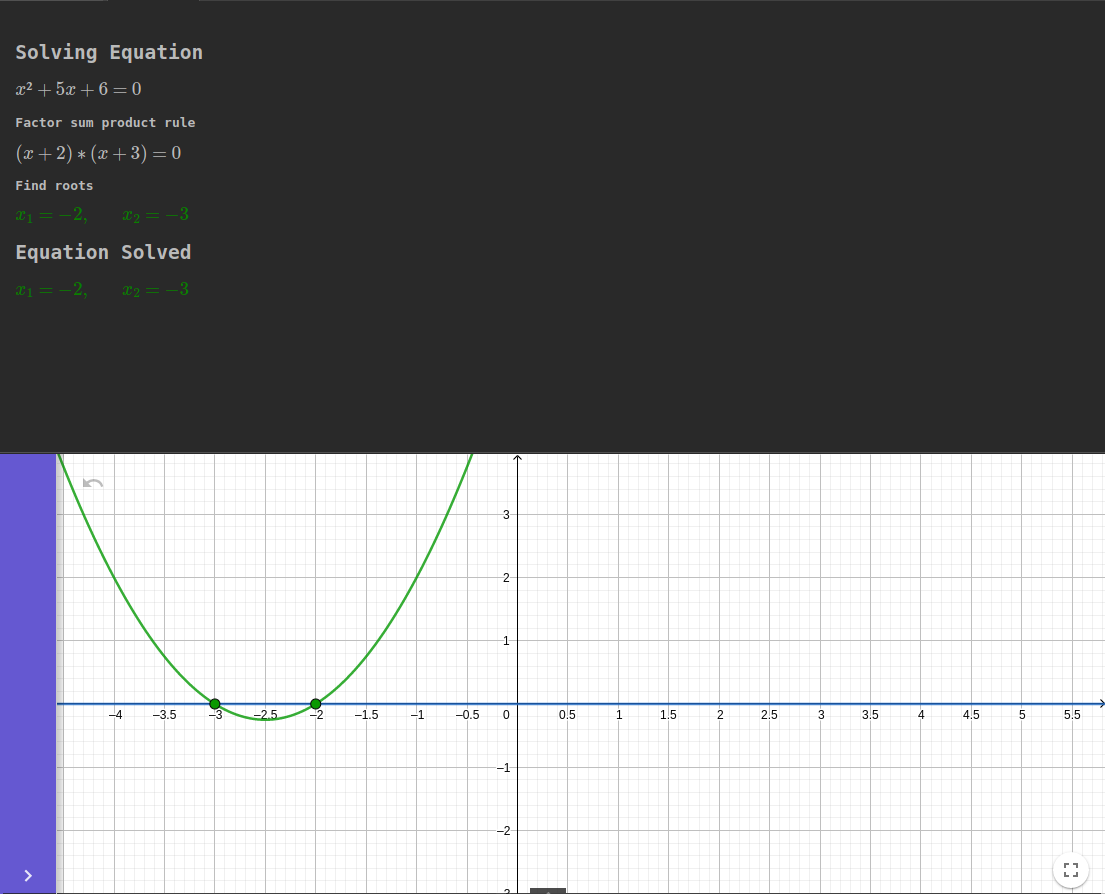
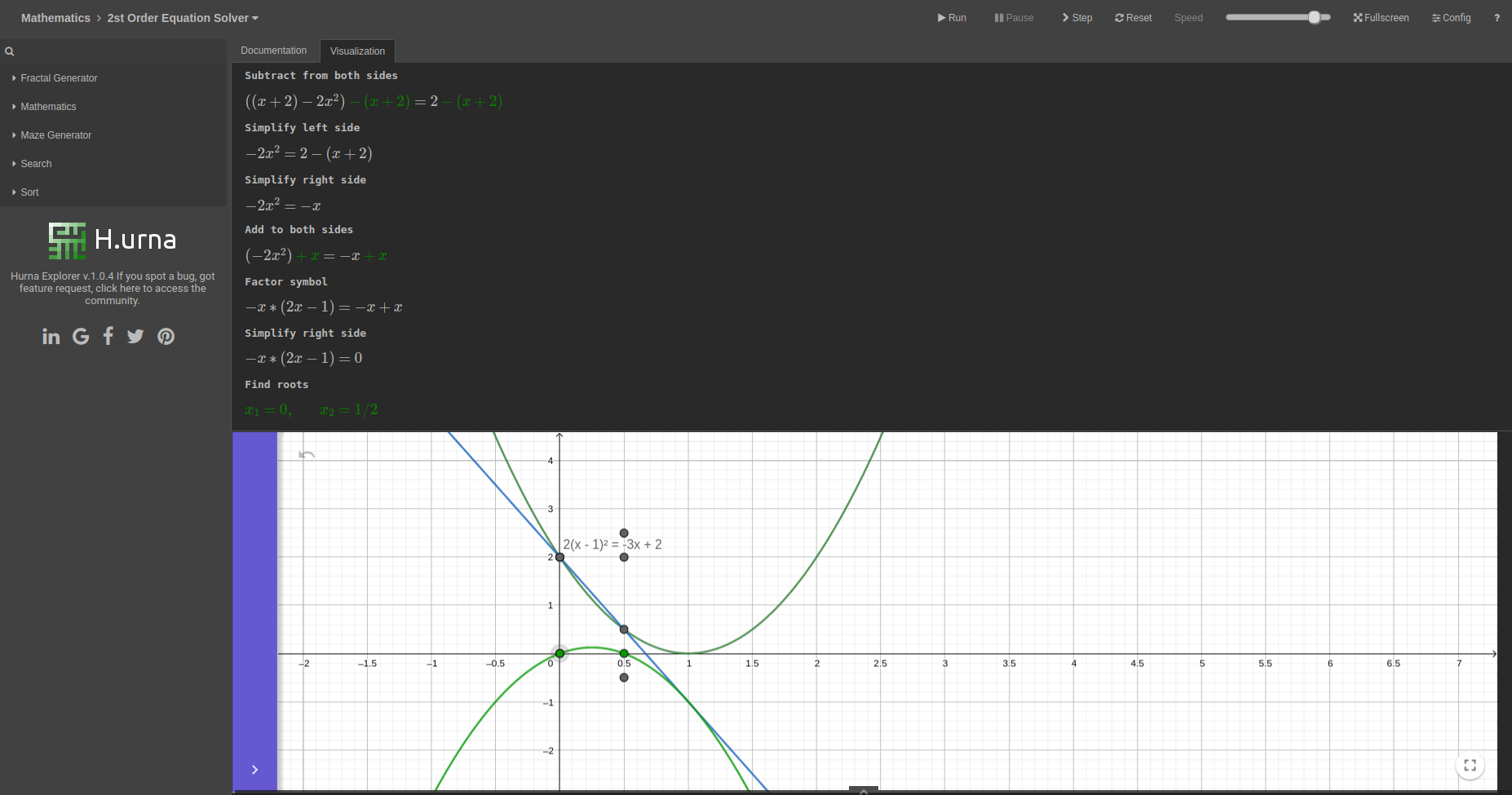
Pour certaines équations, vous pourrez trouver la solution en un clin d'œil s'il existe une forme canonique (cf. outils colonne de droite). Par exemple: $$x² + 5x + 6 = 0$$ Nous pouvons reconnaitre la première forme canonique: $$x² + (a + b)x + ab$$ En effet, si a = 2 et b = 3: $$x² + (2 + 3)x + (2*3) = x² + 5x + 6$$ De ce fait: $$x² + 5x + 6 = (x + 2)(x + 3)$$ Finallement avec la magie de notre outil (cf. troisième colonne de gauche): $$\color{green}{x_1 = -2, \qquad x_2 = -3}$$

C’est le moyen le plus efficace d’obtenir la solution: elle ne nécessite aucun calcul. Cependant, il n'y a pas toujours une factorisation évidente; aussi, il faut s'entraîner pour être efficace.

Pour être plus précis dans la manière de trouver les facteurs (avec ax² + bx + c), vous devez trouver deux nombres n1 et n2 tel que: $$n_1*n_2 = a*c$$ $$n_1+n_2 = b$$

Autrement, utiliser la Formule Quadratique

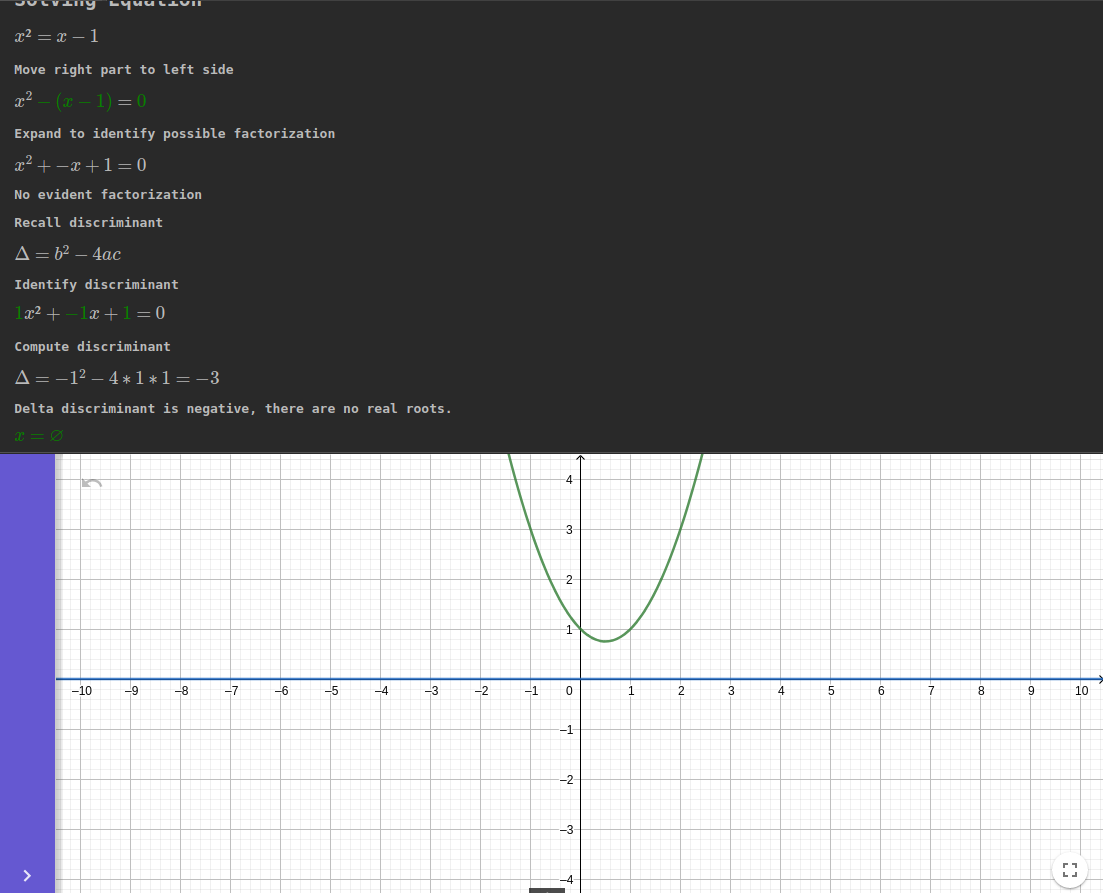
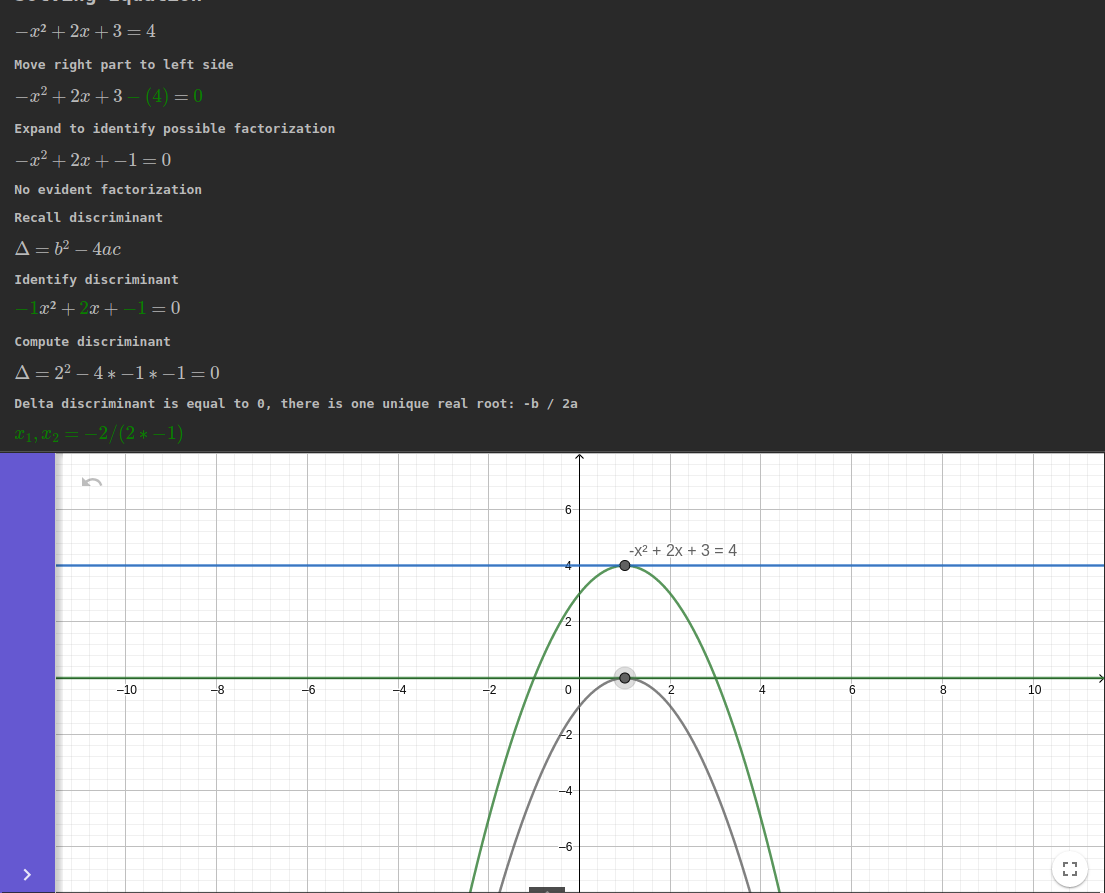
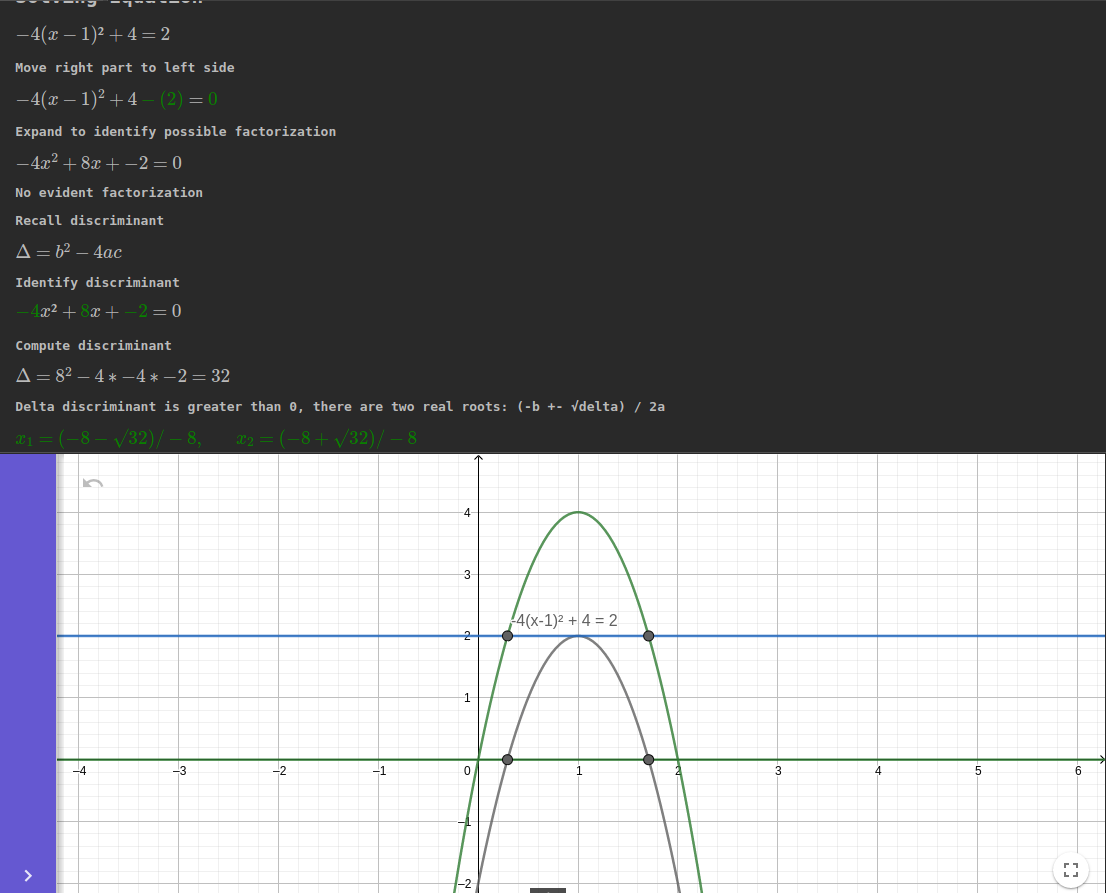
C'est la solution générale de toute équation du second degré : cela fonctionne dans tous les cas possibles. Une équation quadratique peut avoir deux racines distinctes, une seule (appelée racine répétée ou racine double) voire aucune solution (sans inclure les nombres complexes) : trois cas possibles.

Tout d'abord, nous calculons le discriminant delta: $$\Delta = b^{2} - 4ac$$

Si Δ > 0, deux racines réelles (2 points d'intersections): $$x_1={\frac {-b+{\sqrt {\Delta }}}{2a}} \qquad {\text{et}} \qquad x_2={\frac {-b-{\sqrt {\Delta}}}{2a}}$$

Si Δ = 0, une racine double (1 point d'intersection): $$x=-{\frac {b}{2a}}$$

Si Δ < 0, aucune solution (pas d'intersection): $$x=\varnothing$$

Vérifier la solution

Comme d'habitude, nous n'oublions pas de vérifier la solution (Remplacer «x» par la valeur de la solution dans l’équation).

Voici une résolution d’équation étape par étape réalisée par notre professeur virtuel Globo.

Résoudre l'équation x² + 5x + 6 = 0 (celle vue plus haut).
Globo trouve la forme canonique et fait la factorisation (x + a)*(x + b) avec a = -2 et b = -3

Résoudre l'équation x² = x - 1 (ou x² - x + 1 = 0).
Pas de factorisation évidente.
Δ < 0: pas de solution réelle.

Résoudre l'équation -x² +2x + 3 = 4 (ou -x² + 2x - 1 = 0).
Pas de factorisation évidente.
Δ = 0: une solution unique x = 1

Résoudre l'équation -4*(x-1)² + 4 = 2 (ou -4x² + 8x - 2 = 0).
Pas de factorisation évidente.
Δ > 0: deux solutions réelles: $$x_1 = (-8- √32) / -8, \qquad x_2 = (-8+ √32) / -8$$

Exemple réel : Calculer des trajectoires sur Terre

Vous allez utiliser certains préceptes de Newton et résoudre des équations quadratiques, n’ayez pas peur, restez avec nous, tout va bien se passer!

La mascotte Globo mesure 3 m et lance doucement une balle, à une vitesse de 10 m/s (36 km/h), il se demande combien de temps la balle mettra à revenir dans sa main:

L'axe des ordonnées représente l'altitude de la balle (en mètres).
L'axe des abscisses représente le temps en secondes.
La flèche représente la vitesse à laquelle Globo lance la balle.

Combien de temps Globo doit-il attendre que la balle revienne dans sa main ?

Une équation cinématique (synonyme de formule du mouvement ou de trajectoire) sera utilisée. Cependant, il n'est pas indispensable de la comprendre pour l'utiliser.

Equations cinématiques

Voici l'équation donnant la position verticale de la balle (h) à tout moment (t):
$$h = –\frac{1}{2}Gt² + v_0t + h_0$$

Nous remplaçons h par y et t par x pour une lecture plus facile :
$$y = -\frac{1}{2}Gx² + v_0x + y_0$$

Ce que cette équation nous dit :

Maintenant, si nous plaçons simplement les variables connues dans l’équation (nous approximons ici ½G ~ 5 m/s²):
$$y = -5x² + 10x + 3$$

Woooo…. Exactement la forme d'une équation quadratique!

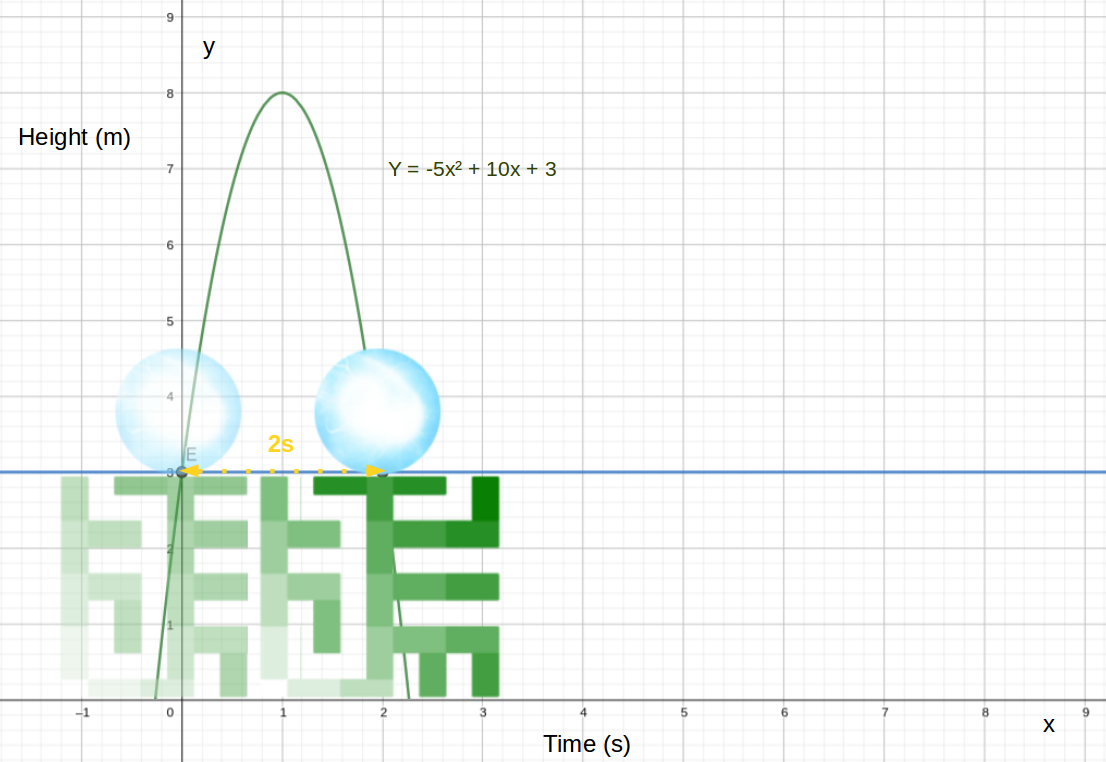
La réponse peut être lue directement à partir du graphique (la balle reste 2s en l'air). Si nous vérifions rapidement:
$$3 = -5 * (2 * 2) + 10 * 2 + 3 = -20 + 20 + 3 = 3 \qquad Parfait !$$ Cependant, la plupart du temps, il sera beaucoup plus difficile d'obtenir une réponse précise à partir du graphique. Pas de soucis, vous savez déjà comment résoudre de telles équations avec l'algèbre pour obtenir la solution précise ;)

Sautez dans l'H.urna Explorer pour résoudre et visualiser les équations du second degré avec notre professeur virtuel Globo.