Une liste de contiguïtés (Adjacency Lists) représente un graphe (ou un arbre) sous la forme d'un tableau de nœuds qui inclut sa liste de connexions. Voyons d'abord à quoi cela ressemble avec un graphe et sa représentation équivalente en utilisant une liste d'adjacences (Adjacency Lists):

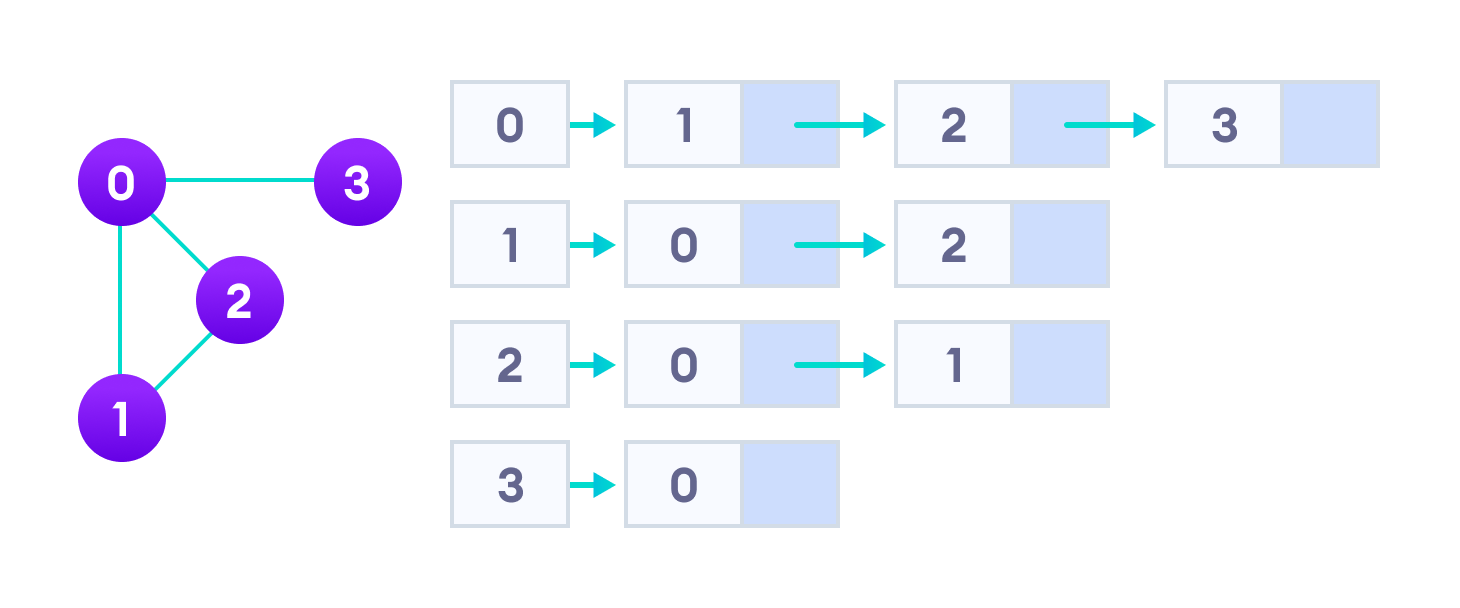
L'idée est assez simple: l'index du tableau représente un nœud et chaque élément de sa liste représente une connexion sortante avec un autre nœud. Facile à créer, facile à manipuler, voici comment les données pourraient être représentées en JSON:

[
  [1, 2, 3],
  [0, 2],
  [0, 1],
  [0]
] 

Oui, c’est aussi simple que cela! Il comprend toutes les informations dont nous avons besoin pour parcourir et visualiser des graphes ou des arbres. C'est par exemple la structure de données que nous avons choisi pour gérer nos labyrinthes:

Applications

L'avantage la liste d'adjacences est qu'elle nous permet de représenter de manière compacte un graphe clairsemé. Elle nous permet également de trouver facilement tous les liens qui sont directement connectés à un nœud particulier et est utiliséé dans des endroits comme: BFS, DFS, Dijkstra, A* (A-Star) etc.

Note: les graphes denses sont ceux qui ont un grand nombre de connexions et les graphes éparses sont ceux qui ont un petit nombre de connexions.

Pour un graphe clairsemé avec des millions de noeuds et de liens, cela peut signifier beaucoup d'espace mémoire économisé.

Parfait, nous savons tout pour créer et manipuler nos graphes!

Manipuler les "Adjacency Lists" et les Graphes.
Créer nos propres structures de graphes.
Comprendre les algorithmes de parcours de graphe.
Comprendre les avantages par rapport à une matrice de contiguïtés.

Et ensuite?

Si vous n'avez pas encore parcouru les algorithmes de générations de labyrinthes, jouer avec eux et utiliser notre explorer vous donne un aperçu visuel des listes de contiguïté. Nous étudierons bientôt plus de structures de données de graphes telle que la matrice de contiguïté qui peut être utile dans des cas particuliers.

Pour modéliser cela en C ++, nous pouvons créer une classe appelée Node , qui a deux variables membres:

- data: Toutes les données supplémentaires que vous souhaitez stocker
- neighbours: Liste des connexions sortantes (en utilisant l'index comme id)

  struct Node
  {
    Node(const T& data, set< int > connexions) : data(data), neighbours(connexions) {}

    T data;                // Any extra data you want to store
    set< int > neighbours; // List of outgoing connexions (using index)
  };

  class Graph
  {
  public:
    Graph(vector< Node > nodes) : nodes(nodes);

  private:
    vector< Node > nodes; // All nodes contained in the graph
  };

Créons un graphe bidirectionnel!

  typedef Node< string > NodeT; // We choose to store the name's node

  auto graph = Graph({
                  NodeT("Globo", {1, 2, 3}),
                  NodeT("Whisky", {0}),
                  NodeT("Hybesis", {0, 1}),
                  NodeT("Boudou", {1, 2})});

Ouais, c'est tout!
Génial. Puisque nous avons tout ce dont nous avons besoin, définissons quelques méthodes utiles.

  // Manipulations
  int Insert(Node node);                         // Insert a node
  void Connect(int idxA, int idxB, bool isBoth); // Add a connexion between two nodes

  // Node Information
  int GetDegree(int idx);             // Return the degree of a node
  set< int > GetNeighbors(int idx);   // Return all the outgoing connexions from a node
         

Manipulations

Insert / Connect

  // Insert a new node and return it's id
  int Insert(Node data)
  {
    nodes.push(data);
    return nodes.size() - 1;
  }

  // Connect two nodes together
  void Connect(int idxA, int idxB, bool isBoth)
  {
    [...] // Checks indexes validity
    nodes[idxA].insert(idxB);
    if (isBoth) nodes[idxB].insert(idxA);
  }
         

Assez facile, non?!

Information des noeuds

GetDegree / GetNeighbors

  // Return the degree of a node (number of connexions)
  int GetDegree(int idx)
  {
    [...] // Checks index validity
    return node[idx].neighbours.size();
  }

  // Get all outgoing connexions of a node
  set< int > GetNeighbors(int idx)
  {
    [...] // Checks index validity
    return nodes[idx].neighbours;
  }
        

À partir de celui-ci, nous pouvons facilement connaître le nombre total de nœuds connectés à n'importe quel nœud et quels sont ces nœuds.

Finissons le codage en implémentant un parcours de graphe. Nous utiliserons un simple BFS (Breadth First Search) directement dans notre classe 'Graph'.

  // We use the bool "isVisited" to keep track of our traversal
  typedef Node< bool > NodeT;

  BFS(int startIdx)
  {
    auto start = nodes.data()[startIdx];  // Get the start node
    start->data = true;                   // Set node to be visited
    Queue queue(start);                   // Put node in the queue

    // While there is node to be handled in the queue
    while (!queue.empty())
    {
      // Handle the node in the front of the line and get unvisited neighbors
      auto node = queue.pop();

      // Take neighbours, mark as visited, and add to the queue
      auto neighbors = node->GetNeighbors();
      for (auto it = neighbors.begin(); it !== neighbors.end(); ++it)
      {
        auto linkedNode = nodes.data()[*it]; // Retrieve neighbor node
        if (linkedNode->data) continue;      // Check if already visited

        linkedNode->data = true;    // Set visited
        queue.push(linkedNode);     // Add to the queue
      }
    }
  }
        

Voila ! Vous pouvez coder un GPS maintenant.

Et si je veux ajouter des poids (distances)?

Les listes de contiguïté peuvent également être utilisées pour représenter un graphe pondéré. Les poids des arêtes (liens / connexions) peuvent être représentés sous forme de listes de paires:

[
  [{ "idx": 1, "weight": 4 }, { "idx": 2, "weight": 2 }, { "idx": 3, "weight": 0 }],
  [{ "idx": 0, "weight": 3 }, { "idx": 2, "weight": 3 }],
  [{ "idx": 0, "weight": 4 }, { "idx": 1, "weight": 4 }],
  [{ "idx": 0, "weight": 10 }]
] 

Essayez de l'implémenter vous-même en tant qu'exercice et essayez de trouver le chemin le plus court dans ce nouveau graphe. Vous pouvez utiliser une version légèrement modifiée de notre algorithme BFS vu ci-dessus.

La listes d'adjacences et la matrice d'adjacences sont les deux représentations les plus couramment utilisées d'un graphe. Comparons-les brièvement avec:

- N le nombre de nœuds.
- M le nombre d'arêtes (connexions).
- degree(i) désigne le nombre de connexions sortantes depuis le nœud i.

Adjacency Lists
Espace mémoire: O(N + M)
Vérifiez si deux nœuds sont connectés: O(degree(i))
Obtenir toutes les connexions sortantes d'un nœud: O(1)

Adjacency Matrix
Espace mémoire: O(N * N)
Vérifiez si deux nœuds sont connectés: O(1)
Obtenir toutes les connexions sortantes d'un nœud: O(N)

Pour les plus courageux, nous finirons par voir un compromis entre l’utilisation du vector (array), du set ou de la liste (linked list) de la STL pour représenter notre graphe. Passons d'abord en revue quelques différences principales:

Set
Un 'set' est automatiquement trié
Insert/Delete/Find: O(log n)

Unordered Set
Un 'unordered set' n'est pas trié
Insert/Delete/Find: O(1)

Vector (Tableau)
Un 'vector' n'est pas trié
Insert/Delete/Find: O(n)

Linked List (Liste Chaînée)
Une 'list' n'est pas trié
Find prends O(n)
Insert/Delete: O(1)

Sur cette base, si nous souhaitons garder nos arêtes (connexions) ou sommets (noeuds) triés, nous devrions probablement choisir un set. Si nous voulons un temps de recherche très rapide, nous pouvons choisir un unordered_set.

Si la recherche n'est pas si importante que cela, nous pouvons utiliser une 'list' (liste) ou un 'vector' (tableau). Mais il y a une autre raison importante pour laquelle on pourrait utiliser un vector / list, qui est pour la représentation de multigraphes.

Un multigraphe est similaire à un graphe, mais il peut avoir plusieurs connexions entre deux nœuds.